Chargement de l'article...
Écriture : Florian Massip
Relecture scientifique : Corentin Dechaud
Relecture de forme : Alexandre Fauquette et Eléonore Pérès
Temps de lecture : environ 10 minutes.
Thématiques : Bioinformatique, Génétique & Épigénétique, Oncologie (Biologie)
Publication originale : Alexandrov L. B., et al., Deciphering Signatures of Mutational Processes Operative in Human Cancer. Cell Reports, 2013. DOI : 10.1016/j.celrep.2012.12.008

Les substances cancérigènes attaquent l’ADN de nos cellules. En perturbant leur bon fonctionnement, elles entraînent la formation de cancers. Mais les mécanismes de formation de ces mutations restent mal compris. En analysant des données de séquençage d’ADN tumoral à l’aide de méthodes statistiques développées pour l’analyse d’images, des scientifiques ont pu décomposer les différentes sources de mutations à l’œuvre dans les cancers, une étape indispensable à la compréhension des causes des mutations, et donc, des cancers.
Mutations et cancer : des bugs dans la Matrice
La publication dont nous allons parler s’intéresse aux substances qui attaquent le génome de nos cellules. Le génome, c’est l’ensemble de l’information génétique d’un individu. C’est un grand plan, dont chaque cellule possède une version identique, qui est lu et interprété par nos cellules et dicte leur fonctionnement. Ce plan définit à la fois le sexe d’un individu [*], la couleur de ses cheveux, son nombre de doigts de pieds, et contient également tout un tas d’informations permettant aux cellules de remplir leurs fonctions : se reproduire, respirer, interagir avec les autres cellules, etc. Comme le plan d’un meuble Ikea, certaines des informations contenues dans le génome sont essentielles au bon fonctionnement de la cellule, tandis que d’autres sont plus superflues : il y a même une grande fraction du génome pour laquelle on n’a trouvé aucune fonction à ce jour ! (À vous aussi il reste toujours trente-six vis dont vous ne savez que faire quand vous avez fini de monter votre meuble ?!)
À la différence d’un plan Ikéa, le génome n’est pas inscrit sur du papier mais sur une très longue molécule, l’acide désoxyribonucléique ou ADN. Chaque molécule d’ADN est un long assemblage de briques élémentaires (appelées nucléotides), dont il existe quatre types différents : l’adénine (A), la cytosine (C), la guanine (G) et la thymine (T). Ainsi, on peut représenter le génome d’un humain comme un long texte de trois milliards de lettres, écrit dans un alphabet de quatre lettres : A, C, T et G.
Au départ, le génome de l’ensemble des cellules d’un individu est identique. Toutefois, au cours de la vie, le génome de certaines des cellules peut être altéré par des mutations. Une mutation se produit lorsqu’un nucléotide du génome est remplacé par un autre [**]. Lorsque la mutation a lieu sur une partie du texte qui n’est pas indispensable au fonctionnement de la cellule (ce qui est le cas la majorité du temps [1]), la cellule peut continuer sa vie comme si de rien n’était. Mais il arrive qu’une ou plusieurs mutations atteignent des zones importantes du génome. Dans ce cas, les mutations peuvent entraîner le dysfonctionnement de la cellule. C’est ce phénomène qui est à l’origine de la plupart des cancers.
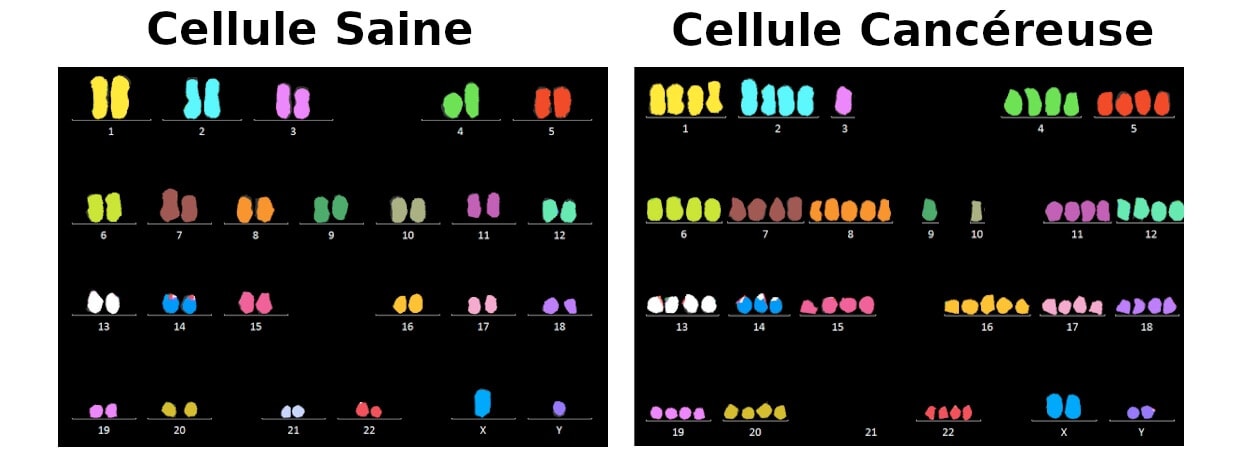
En fait, le génome des cellules cancéreuses est généralement très fortement perturbé et présente des dizaines voire des centaines de milliers de mutations [2] ! On peut même observer ces perturbations en observant le génome de cellules cancéreuses au microscope (Figure 1).
L’origine des mutations
On sait que les cellules cancéreuses présentent de très nombreuses mutations, mais comment apparaissent-elles ? Il y a de nombreuses causes possibles à la formation de mutation en général, mais les causes de l’apparition des mutations dans les cancers ne sont pas bien connues. Par exemple, lorsque nos cellules se divisent, elles font une copie de leur ADN. Cela permet aux cellules créées d’avoir leur propre copie. Comme nul n’est infaillible, il se peut que des coquilles se glissent lors de la recopie. Par ailleurs, certaines substances cancérigènes auxquelles nous sommes exposées (la fumée de cigarette par exemple, certains produits chimiques, ou encore des virus ou des bactéries) attaquent directement l’ADN contenu dans nos cellules et provoquent des mutations. Enfin, il y a les mutations qui se produisent spontanément au cours de la vie, sans cause particulière autre que le vieillissement.
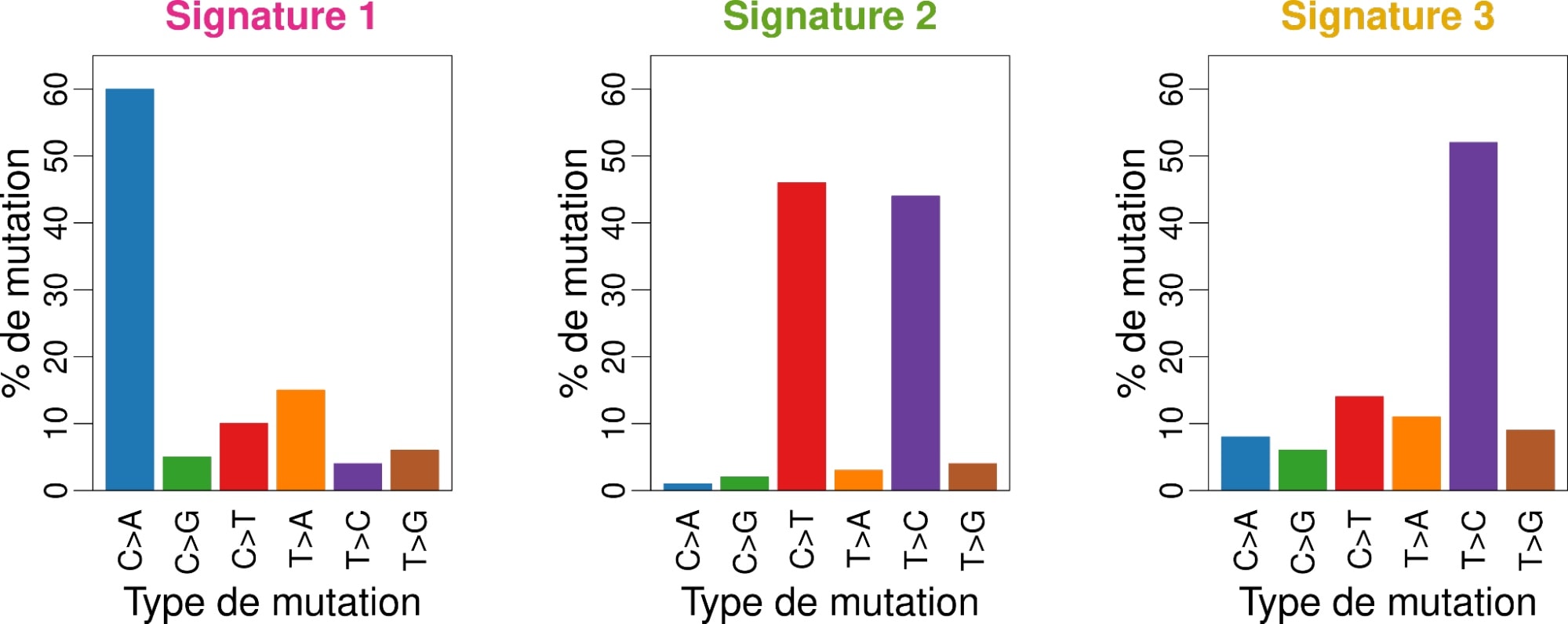
Ces sources de mutation sont appelées agents mutagènes. Ils ont chacun leur petite préférence : la fumée de cigarette transforme les cytosines en adénines (que l’on note C>A pour « C devient A »), alors que les UV ont davantage tendance à transformer les C en T. Plus précisément, ces agents mutagènes attaquent tous les nucléotides mais ont souvent une préférence pour un ou plusieurs types de mutations : environ 60 % des mutations provoquées par la fumée de cigarette sont du type C>A, 15 % sont du type T>A, 10 % sont du type C>T et ainsi de suite. Pour les UV, on a 45 % de C>T, 45 % de T>C et très peu d’autres types de mutations. Chaque agent mutagène provoque donc une combinaison de mutations qui lui est propre, avec des proportions bien particulières. On appelle la signature de mutation d’un agent mutagène la proportion de chaque type de mutation que ce processus génère (Figure 2).
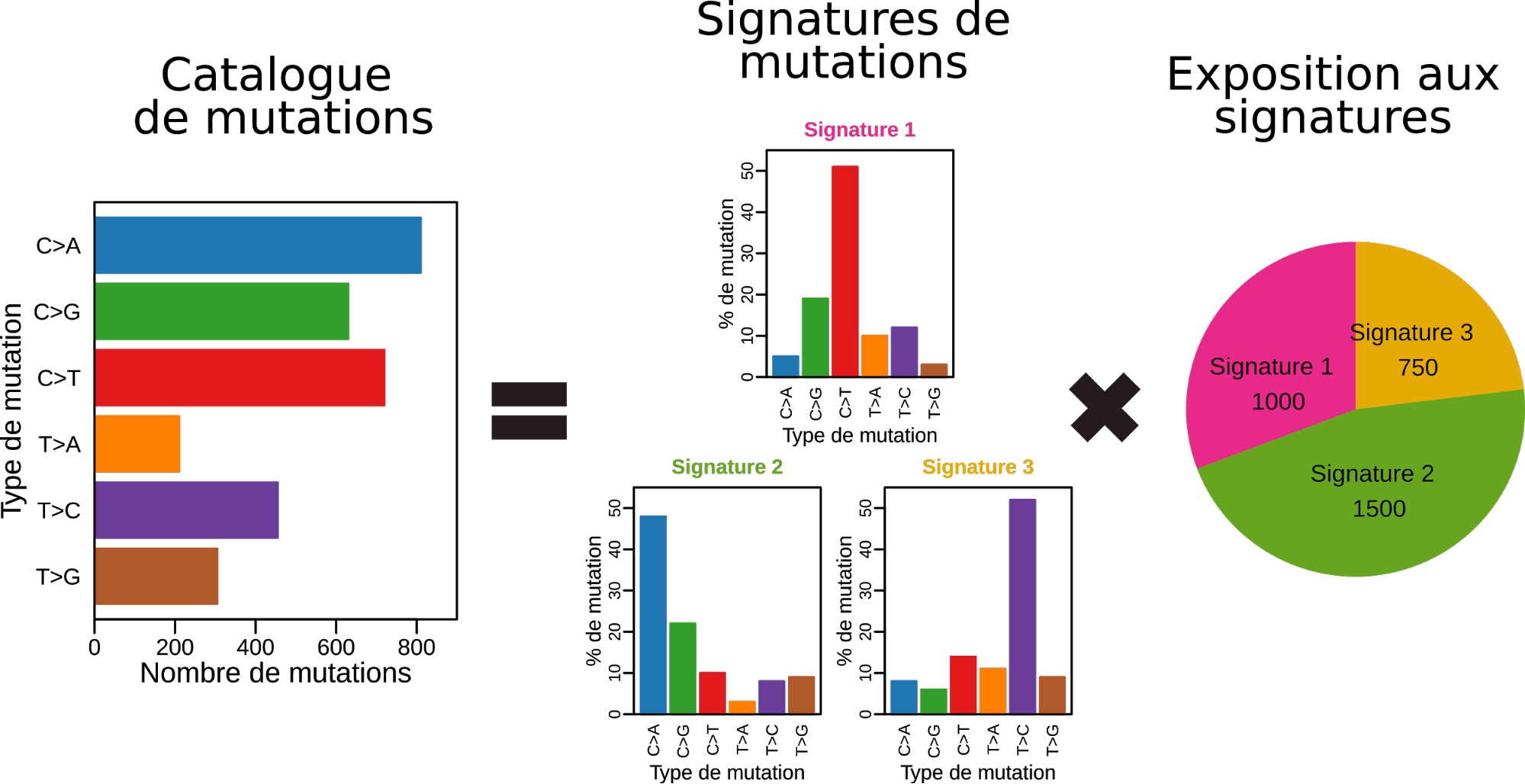
Bien que l’on connaisse de nombreux agents mutagènes à l’origine de mutations (traitements médicaux comme les chimiothérapies, exposition à des substances chimiques, certaines bactéries, etc.), on ne sait pas quels types de mutations la plupart de ces processus mutagènes provoquent en majorité. C’est à cette question que la publication présentée ici tente de répondre. Pour cela, les auteurs de l’étude ont utilisé des données de séquençage de l’ADN tumoral (une technique consistant à extraire l’ADN des cellules tumorales puis à « lire » le génome lettre après lettre afin d’obtenir le génome des tumeurs) provenant de 21 patientes atteintes de cancer du sein. Pour chacune de ces patientes, ils ont construit un catalogue de mutations qui décrit l’ensemble des mutations génétiques ayant eu lieu dans leur cancer respectif, en comptant, pour chaque patiente, le nombre de mutations de chaque type (C>A, C>T, T>G, etc.) présent dans sa tumeur.
La résolution de ce problème est particulièrement difficile. Dans chaque cancer, de nombreuses sources de mutations sont à l’œuvre en même temps : il y a des mutations dues au vieillissement (dont le nombre dépend de l’âge de la patiente), des mutations dues à la fumée de cigarette (dont le nombre dépend de la quantité de cigarette consommée par la patiente), des mutations dues aux différents traitements qu’elle a subis, etc. Le catalogue de mutation d’une patiente est donc comparable à un pot-pourri de mutations causées par plein de processus différents. Le but de la méthode introduite par cet article est de démêler et d’identifier les différentes sources de mutations.
Qu’est-ce que la Matrice ? Les données du problème
C’est ici qu’interviennent les matrices. Comment ? me direz-vous ; et puis d’abord, qu’est-ce qu’une matrice ? « Matrice », c’est juste un mot savant pour dire « tableau à double entrée » (Figure 3).
C’est une manière assez pratique de représenter les données de l’article : on a une ligne par patiente, une colonne par type de mutation et dans chaque case est noté le nombre de mutations du type donné pour la patiente donnée. Dans notre cas, c’est un relativement petit tableau avec 21 lignes et 12 colonnes, mais pour des problèmes plus complexes et des jeux de données plus importants, les matrices peuvent être proprement gigantesques. Par exemple, une image en noir et blanc dans un ordinateur, c’est une très grande matrice. Chaque case contient une valeur qui est grande si le point est blanc et petite si le point est sombre (et plus on a de valeurs, plus la résolution de l’image est grande). Pour analyser automatiquement ces très grandes matrices, les informaticiens et les statisticiens ont inventé des algorithmes, c’est-à-dire des programmes informatiques.
Pour reprendre le cas d’une image, ces algorithmes sont par exemple capables de reconnaître et de séparer les différentes parties qui constituent un visage (les yeux, le nez, la bouche, etc.) à force d’entraînement sur un grand nombre d’images de visage. L’idée (géniale !) des auteurs de cet article a été d’appliquer une de ces méthodes d’analyse d’image à la matrice de mutations de la Figure 3. En effet si, au lieu de donner à l’algorithme des images de visage, on lui présente une matrice contenant des catalogues de mutations qui se sont produites dans des cancers, il va être capable d’identifier des similitudes entre les génomes des patientes. Ici, ce ne sont pas des nez ou des yeux, mais justement les processus mutagènes communs aux différents cancers qui ont laissé des signatures similaires dans les génomes des cancers des différentes patientes. Les mathématiques, c’est magique n’est-ce pas ?! Pour l’anecdote, l’algorithme utilisé ici s’appelle la factorisation en matrice non-négative (pour non-negative matrix factorization en anglais).
Lire entre les lignes (de la Matrice) : un problème d’interprétation
En pratique, l’algorithme ne sait pas ce qu’est un œil, n’a aucune idée de ce qui définit un visage, ni ce qu’est une signature de mutations. Simplement, quand on lui présente de nombreux visages et qu’on lui demande : « Donne-moi les points communs entre les images que je t’ai montrées », il est capable d’identifier que dans chaque image, il y a deux formes claires un peu ovales avec un rond sombre au centre. Il faut ensuite qu’un humain analyse le résultat et reconnaisse que cette structure est un œil. Dans le cas des signatures de mutations, c’est un peu la même chose. L’algorithme va être capable de nous dire : « Je reconnais qu’il y a un processus qui produit beaucoup de mutations C>T dans les génomes des cancers des patients que tu me montres ». Mais ensuite, il faut un humain pour interpréter les résultats et relier ces signatures à des agents mutagènes particuliers.
Par exemple, en utilisant les génomes de cancer des 21 patientes, les chercheurs ont pu identifier 4 signatures de mutations. La première correspond à un processus de mutation bien connu dû au vieillissement des cellules. La seconde était inconnue avant la publication de l’article, mais les auteurs ont pu identifier que cette signature était particulièrement active seulement chez 9 des 21 patientes. Or, en analysant les données médicales de ces 9 patientes, ils se sont rendu compte qu’elles avaient toutes la même anomalie génétique héréditaire, ce qui leur a permis de faire l’hypothèse que cette anomalie génétique serait un facteur qui favorise l’accumulation de mutations dans les cellules cancéreuses (voir aussi [3]). Mais il a fallu conduire des expériences complémentaires pour confirmer ce résultat. Enfin, pour une des signatures, ils n’ont pas pu trouver le processus à l’origine des mutations [***].
Ainsi, la méthode présentée dans cet article permet d’identifier des signatures de mutations actives dans les cancers. Mais ce faisant, elle pose la question de savoir qui sont les agents mutagènes à l’origine de ces mutations. En effet, en utilisant cette méthode avec les données de milliers de patients, un article récent a pu identifier plus de 70 signatures de mutations [4]. Mais l’agent mutagène responsable de ces signatures n’est connu que pour la moitié d’entre elles ! L’identification des autres agents mutagènes nécessitera de nombreuses études. La méthode développée dans cet article a ainsi ouvert un large champ de recherche, comme c’est souvent le cas avec les publications scientifiques les plus influentes !
[*] À noter que des études récentes remettent en cause le modèle classique qui veut que le sexe d’un individu soit purement déterminé par son nombre de chromosomes X. Voir par exemple cet article (en anglais).
[**] Pour des raisons de simplifications, nous ne parlons dans cet article que des mutations ponctuelles (un nucléotide remplacé par un autre). Mais il en existe de nombreuses variétés que l’on classe en quatre grands types : les mutations ponctuelles, les insertions et délétions de petite taille (de 1 à 10 000 nucléotides), les insertions et délétions de grande tailles (pouvant concerner un chromosome entier) et les réarrangements (lorsque de longs fragments du génome changent de place, comme par exemple en sautant d’un chromosome à un autre). Jusqu’à récemment, on ne portait pas beaucoup d’attention aux mutations autres que les mutations ponctuelles, notamment parce que ce sont les plus faciles à identifier. Pourtant, l’impact des autres types de mutations, notamment dans les cancers, est aujourd’hui l’objet de nombreuses études.
[***] Une fois que l’on a identifié une signature de mutations active dans un cancer, il reste encore à identifier le processus à l’œuvre. Même si une signature est très bien identifiée dans de nombreux cas de cancer, si l’on ne connaît pas le facteur commun entre tous les patients qui présentent cette signature, on ne peut pas deviner l’agent en cause. Pour cela il faut, en plus du séquençage du génome, mener des études épidémiologiques précises puis valider l’effet mutagène des agents candidats avec des études de biochimie.
[1] Lindblad-Toh K., et al., A high-resolution map of human evolutionary constraint using 29 mammals. Nature, 2011. DOI : 10.1038/nature10530. [Publication scientifique]
[2] Lawrence M., et al., Mutational heterogeneity in cancer and the search for new cancer-associated genes. Nature, 2013. DOI : 10.1038/nature12213. [Publication scientifique]
[3] Nik-Zainal S., et. al., Mutational Processes Molding the Genomes of 21 Breast Cancers. Cell, 2012. DOI : 10.1016/j.cell.2012.04.024. [Publication scientifique]
[4] Alexandrov L. B., et. al., The repertoire of mutational signatures in human cancer. Nature, 2020. DOI : 10.1038/s41586-020-1943-3. [Publication scientifique]
Écriture : Florian Massip
Relecture scientifique : Corentin Dechaud
Relecture de forme : Alexandre Fauquette et Eléonore Pérès
Temps de lecture : environ 16 minutes.
Thématiques : Bioinformatique, Génétique & Épigénétique, Oncologie (Biologie)
Publication originale : Alexandrov L. B., et al., Deciphering Signatures of Mutational Processes Operative in Human Cancer. Cell Reports, 2013. DOI : 10.1016/j.celrep.2012.12.008

Les substances cancérigènes attaquent l’ADN de nos cellules. En perturbant leur bon fonctionnement, elles entraînent la formation de cancers. Mais les mécanismes de formation de ces mutations restent mal compris. En analysant des données de séquençage d’ADN tumoral à l’aide de méthodes statistiques développées pour l’analyse d’images, des scientifiques ont pu décomposer les différentes sources de mutations à l’œuvre dans les cancers, une étape indispensable à la compréhension des causes des mutations, et donc, des cancers.
Mutations et cancer : des bugs dans la Matrice
Un des signes distinctifs des cellules cancéreuses est de présenter de très nombreuses mutations génétiques, de sorte que l’on qualifie parfois les cancers de « maladie du génome ». Les mutations somatiques présentes dans les cellules cancéreuses se produisent tout au long de la vie de l’individu, et sont à distinguer des mutations germinales, héritées des deux parents, et qui peuvent être à l’origine de maladies génétiques. Parmi les mutations somatiques, on peut distinguer deux grandes catégories : les mutations n’ayant pas d’effet et les mutations fonctionnelles, qui, par leur présence, vont perturber plus ou moins fortement le fonctionnement de la cellule. Ces dernières ont des conséquences diverses plus ou moins graves et jouent un rôle dans la formation de cancers. Par analogie, on qualifie les mutations sans conséquences fonctionnelles de « passagères » car, comme les passagers d’une voiture, elles n’ont pas de rôle actif dans le développement du cancer, et les mutations qui ont des conséquences fonctionnelles de « conductrices » (driver mutations en anglais).
Comme la vaste majorité (90-95 %) des nucléotides de notre génome n’a pas de fonction vitale indispensable au fonctionnement de la cellule [1], la plupart des mutations présentes dans les cancers sont des mutations passagères. De plus, comprendre les effets des mutations observées dans les cancers et identifier les fameuses mutations conductrices n’est pas une mince affaire et cette thématique fait l’objet de très nombreuses études. La publication présentée ici ne s’intéresse donc pas à cette question. Le but ici est de comprendre comment apparaissent les mutations dans les cancers — qu’elles soient conductrices ou passagères, car les mécanismes de leur formation sont les mêmes — afin de mieux appréhender les causes de la formation des cancers.
L’origine des mutations
si l’on sait depuis longtemps que les cellules cancéreuses présentent de nombreuses anomalies génétiques, les causes de ces mutations et les mécanismes de leur formation restent mal compris. Par exemple, un mécanisme de mutation bien connu est la déamination des cytosines qui se produit naturellement au cours de la vie des cellules. Elle a pour effet de faire muter ces cytosines (C) en thymine (T). Ce mécanisme provoque l’accumulation de mutations des C vers T (on notera C>T dans la suite de l’article). L’exposition à certaines substances cancérigènes (la fumée de cigarette par exemple) peut également provoquer des mutations. Ces substances s’attaquent tout particulièrement à certaines combinaisons de nucléotides. Notamment, la consommation de cigarettes favorise les mutations du type C>A tandis que l’exposition aux UV provoque des mutations C>T ainsi que CC>TT. On appelle signature de mutation d’un procédé la proportion de chaque type de mutation que ce processus génère.
On a identifié bien d’autres facteurs provoquant des mutations : des traitements médicaux (comme les chimiothérapies), l’exposition à des substances chimiques, certaines bactéries ou encore le dysfonctionnement des mécanismes de réparation de l’ADN. Toutefois, dans la plupart des cas, on ne sait pas quels types de mutations sont associés à chacun de ces processus. C’est à cette question que cet article tente de répondre.
Comme de nombreux processus de mutations sont actifs en même temps dans chaque cancer, il semble difficile d’identifier chacune des signatures à l’œuvre. Résoudre ce problème est en fait un problème classique bien connu en informatique et plus particulièrement en analyse automatique d’images. Les auteurs de cette étude ont ainsi utilisé une méthode existante appelée factorisation en matrice non-négative (ou NMF pour non-negative matrix factorization en anglais) [2] pour résoudre ce problème. Le modèle mathématique que proposent les auteurs de cet article permet à la fois de découvrir les signatures de mutations à l’œuvre dans les cancers et d’estimer le niveau d’exposition à ces signatures chez des patients souffrant de cancers.
Qu’est-ce que la Matrice ? Les données du problème
Les auteurs de l’étude disposent de 21 catalogues de mutations qui décrivent l’ensemble des mutations génétiques ayant eu lieu dans les cancers de 21 patientes atteintes de cancer du sein. Pour chaque patiente, l’ADN d’un échantillon de cellules saines et d’un échantillon de cellules tumorales a été séquencé. Identifier les différences entre le génome des cellules saines et celui des cellules cancéreuses permet d’identifier les mutations qui se sont produites dans les cellules cancéreuses au cours du développement de la tumeur.
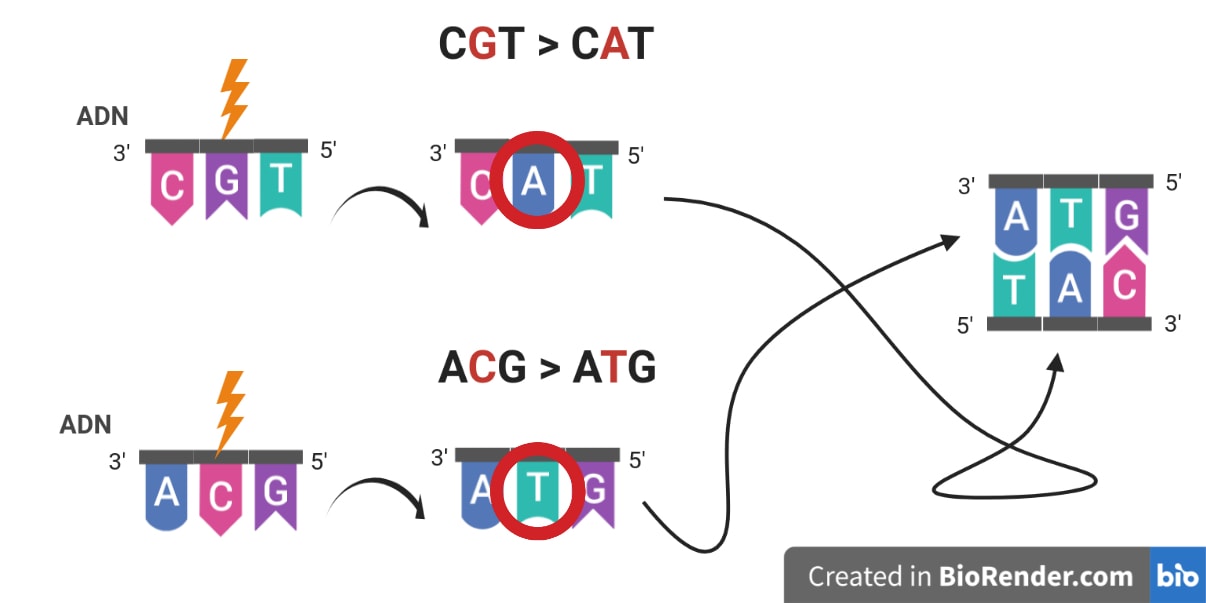
Afin de découvrir des signatures de mutations, les auteurs commencent par classer les mutations en différents types, en ne s’intéressant ici qu’aux mutations ponctuelles affectant un seul nucléotide [*]. Comme l’ADN est composé de 4 types de nucléotides (A, T, C et G) et que chaque nucléotide peut muter en l’un des 3 autres, il existe ![]() types de mutations. Toutefois, du fait de la complémentarité des bases et de la structure en double hélice de l’ADN, chaque mutation est équivalente à sa mutation complémentaire : quand un A mute et devient un C sur l’un des deux brins, sa base complémentaire sur l’autre brin (un T dans ce cas) est également remplacée par un G. Ainsi, les mutations A>C et T>G sont équivalentes (Figure 1). Puisque chaque mutation a une mutation complémentaire, les 12 mutations sont classées en 6 types contenant chacun 2 mutations complémentaires.
types de mutations. Toutefois, du fait de la complémentarité des bases et de la structure en double hélice de l’ADN, chaque mutation est équivalente à sa mutation complémentaire : quand un A mute et devient un C sur l’un des deux brins, sa base complémentaire sur l’autre brin (un T dans ce cas) est également remplacée par un G. Ainsi, les mutations A>C et T>G sont équivalentes (Figure 1). Puisque chaque mutation a une mutation complémentaire, les 12 mutations sont classées en 6 types contenant chacun 2 mutations complémentaires.
Cependant, on sait également que certains couples ou trio de nucléotides sont plus sensibles que d’autres à certains processus. Par exemple, la désamination des cytosines qui entraîne la mutation C>T est beaucoup plus fréquente quand le C est suivi d’un G. Ainsi, les nucléotides voisins affectent le taux de mutation d’un nucléotide donné. En considérant les deux voisins de chaque nucléotide, on a alors quatre possibilités avant et quatre possibilités après le nucléotide, soit ![]() contextes possibles pour chaque mutation. Par exemple, pour la mutation C>T on différencie ACG>ATG, TCG>TTG, ACA>ATA, etc.
contextes possibles pour chaque mutation. Par exemple, pour la mutation C>T on différencie ACG>ATG, TCG>TTG, ACA>ATA, etc.
En résumé, on a 6 types de mutations (12 divisé par deux avec les mutations équivalentes), chacune ayant 16 contextes possibles. Cela fait au total 96 types de mutations différentes. On pourrait d’ailleurs augmenter encore le nombre de types de mutations en s’intéressant aux quintuplets plutôt qu’aux trios. Toutefois, étendre le contexte aux quintuplets augmente le nombre de types de mutations à considérer, rendant le modèle plus complexe et les calculs plus difficiles. Pour chacune des 21 patientes de l’étude, les auteurs se sont donc concentrés sur les trios en comptant le nombre de mutations pour chacun des 96 types de mutations. Ainsi, le résultat de cette analyse est un tableau (ou matrice, notée ![]() ) de 21 lignes (une par patiente) et 96 colonnes (une par type de mutation).
) de 21 lignes (une par patiente) et 96 colonnes (une par type de mutation).
Comment définir mathématiquement une signature de mutation ?
Revenons maintenant au problème que les auteurs cherchent à résoudre : identifier un petit nombre (que l’on va noter ![]() ) de processus biologiques responsables de la formation de ces mutations. En somme, ils cherchent à résumer les 96 types de mutations différentes en un plus petit nombre de sources à l’origine de ces mutations. En effet, chaque source de mutation a une signature de mutation qui lui est propre car certains processus mutagènes s’attaquent plus particulièrement à certains nucléotides. La difficulté du problème vient du fait que les signatures peuvent se recouper. Mathématiquement, on définit une signature de mutation par un ensemble de 96 taux de mutations quantifiant l’importance relative de chaque type de mutation dans cette signature. Chacun des taux est un nombre entre 0 et 1 et la somme des 96 taux vaut 1. Par exemple, si un mutagène provoque uniquement des mutations de ACT en AGT, sa signature sera simplement composée de 95 « zéro » et 1 « un ». Un processus qui attaque tous les trios de nucléotides de manière indifférenciée aura quant à lui pour signature un même taux (1/96) pour chacun des 96 types de mutation.
) de processus biologiques responsables de la formation de ces mutations. En somme, ils cherchent à résumer les 96 types de mutations différentes en un plus petit nombre de sources à l’origine de ces mutations. En effet, chaque source de mutation a une signature de mutation qui lui est propre car certains processus mutagènes s’attaquent plus particulièrement à certains nucléotides. La difficulté du problème vient du fait que les signatures peuvent se recouper. Mathématiquement, on définit une signature de mutation par un ensemble de 96 taux de mutations quantifiant l’importance relative de chaque type de mutation dans cette signature. Chacun des taux est un nombre entre 0 et 1 et la somme des 96 taux vaut 1. Par exemple, si un mutagène provoque uniquement des mutations de ACT en AGT, sa signature sera simplement composée de 95 « zéro » et 1 « un ». Un processus qui attaque tous les trios de nucléotides de manière indifférenciée aura quant à lui pour signature un même taux (1/96) pour chacun des 96 types de mutation.
Par ailleurs, l’exposition aux processus mutagènes varie d’un patient à l’autre. Par exemple, le nombre de mutations observées dans un cancer est proportionnel à la dose d’agent mutagène à laquelle le patient a été exposé [3] : on observe plus de mutations spécifiques de la cigarette dans le génome cancéreux du patient A qui a fumé vingt cigarettes par jours pendant vingt ans, que chez le patient B ayant fumé trois cigarettes par jours pendant deux ans. À l’inverse, si le patient B est trente ans plus âgé que le patient A, le nombre de mutations provoquées par le vieillissement sera plus important chez lui. Le génome du cancer d’un patient est donc le résultat d’une combinaison particulière de différents processus mutagènes d’expositions diverses.
Ainsi, le nombre de mutations d’un type particulier (ACT>AGT par exemple) observé dans le génome du patient ![]() est donné par la somme du taux de mutation ACT>AGT dans la signature 1 (noté
est donné par la somme du taux de mutation ACT>AGT dans la signature 1 (noté ![]() ) multiplié par l’exposition à la signature 1 chez ce patient (noté
) multiplié par l’exposition à la signature 1 chez ce patient (noté ![]() ), additionné du taux de ACT>AGT dans la signature 2 multiplié par l’exposition à la signature 2 chez ce patient, et ainsi de suite pour toutes les signatures (Figure 2). En termes mathématiques, on peut écrire que le nombre de mutations de type
), additionné du taux de ACT>AGT dans la signature 2 multiplié par l’exposition à la signature 2 chez ce patient, et ainsi de suite pour toutes les signatures (Figure 2). En termes mathématiques, on peut écrire que le nombre de mutations de type ![]() chez le patient
chez le patient ![]() vaut :
vaut :
![Rendered by QuickLaTeX.com \[m_{i,r}=\sum_{u=1}^K p_{r,u} \times e_{u,i}\]](https://papiermachesciences.org/wp-content/ql-cache/quicklatex.com-a56b23f56f8834c6d813e1f8410c03ac_l3.png)
La méthode développée dans cet article vise à déterminer à la fois les signatures de mutations (les ![]() de la formule) ainsi que les expositions (les
de la formule) ainsi que les expositions (les ![]() de la formule) de ces processus chez chacune des patientes
de la formule) de ces processus chez chacune des patientes ![]() et pour chaque signature
et pour chaque signature ![]() .
.
Si on écrit l’équation précédente pour chaque patient ![]() et chaque type de mutation
et chaque type de mutation ![]() , on obtient un grand système avec beaucoup d’équations et encore plus d’inconnues. En fait, on peut écrire cet ensemble d’équations sous la forme matricielle suivante :
, on obtient un grand système avec beaucoup d’équations et encore plus d’inconnues. En fait, on peut écrire cet ensemble d’équations sous la forme matricielle suivante :
![]()
où
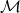 est notre matrice de données comptabilisant le nombre de mutations par patient ;
est notre matrice de données comptabilisant le nombre de mutations par patient ;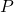 est la matrice des signatures dont chaque entrée
est la matrice des signatures dont chaque entrée 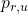 est le taux de mutation de type
est le taux de mutation de type  pour la signature
pour la signature 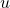 (chaque colonne est ainsi une signature de mutation) ;
(chaque colonne est ainsi une signature de mutation) ; 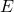 est la matrice d’exposition, dont chaque case
est la matrice d’exposition, dont chaque case 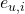 quantifie l’exposition à la signature
quantifie l’exposition à la signature 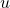 pour le patient
pour le patient 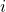 .
.
Notre problème consiste donc à factoriser la matrice ![]() en deux plus petites matrices
en deux plus petites matrices ![]() et
et ![]() [**]. Il se trouve que c’est exactement l’objectif d’une méthode utilisée pour faire de l’analyse automatique d’image, la fameuse factorisation en matrices non-négatives. Comme son nom l’indique, cette méthode s’applique uniquement aux matrices dont l’ensemble des entrées sont positives. Ça tombe bien, les paramètres du modèles que l’on étudie ici (
[**]. Il se trouve que c’est exactement l’objectif d’une méthode utilisée pour faire de l’analyse automatique d’image, la fameuse factorisation en matrices non-négatives. Comme son nom l’indique, cette méthode s’applique uniquement aux matrices dont l’ensemble des entrées sont positives. Ça tombe bien, les paramètres du modèles que l’on étudie ici (![]() ;
; ![]() ;
; ![]() ) sont tous positifs. Cette contrainte sur les paramètres facilite l’identification de solutions et rend également les résultats plus simples à interpréter.
) sont tous positifs. Cette contrainte sur les paramètres facilite l’identification de solutions et rend également les résultats plus simples à interpréter.
Les Matrices parfaites n’existent pas
Très bien ! Mais comment est-ce qu’on les trouve, ces matrices, me demanderez-vous ?! C’est simple : on essaie plein de solutions jusqu’à en trouver une satisfaisante ! Pour commencer, simplifions le problème en étudiant le cas où l’on connaît le nombre de signatures ![]() .
.
En fait, notre problème n’a pas de solution parfaite : on ne trouvera jamais une solution exacte telle que ![]() . Ce que l’on veut, c’est trouver deux matrices
. Ce que l’on veut, c’est trouver deux matrices ![]() et
et ![]() telles que la différence entre
telles que la différence entre ![]() et
et ![]() soit aussi petite que possible. On va noter
soit aussi petite que possible. On va noter ![]() l’estimation de
l’estimation de ![]() . C’est ce qui va nous permettre de juger la qualité de notre solution : plus les valeurs dans la matrice des erreurs
. C’est ce qui va nous permettre de juger la qualité de notre solution : plus les valeurs dans la matrice des erreurs ![]() seront petites, meilleure sera la solution.
seront petites, meilleure sera la solution.
Comme en pratique on ne peut pas tester toutes les solutions possibles, on utilise un algorithme (le multiplicative update algorithm) afin d’explorer l’ensemble des solutions possibles de manière efficace. On commence par générer des matrices ![]() et
et ![]() aléatoires [***]. On calcule alors pour chaque matrice le ratio entre la valeur observée dans la matrice
aléatoires [***]. On calcule alors pour chaque matrice le ratio entre la valeur observée dans la matrice ![]() et la valeur estimée par
et la valeur estimée par ![]() afin de mesurer la qualité de l’estimation. Si l’estimation est de mauvaise qualité, on est loin du but donc on peut modifier largement les matrices
afin de mesurer la qualité de l’estimation. Si l’estimation est de mauvaise qualité, on est loin du but donc on peut modifier largement les matrices ![]() et
et ![]() . Par contre, si l’estimation est de bonne qualité, on a intérêt à ne faire que de petits changements à la marge. Dans les faits, pour chaque terme des matrices
. Par contre, si l’estimation est de bonne qualité, on a intérêt à ne faire que de petits changements à la marge. Dans les faits, pour chaque terme des matrices ![]() et
et ![]() , on regarde s’il vaut mieux l’augmenter ou le diminuer pour que la distance entre l’estimation
, on regarde s’il vaut mieux l’augmenter ou le diminuer pour que la distance entre l’estimation ![]() et les données
et les données ![]() diminue. À chaque itération de l’algorithme, on met ainsi à jour les valeurs de chacun des termes des matrices
diminue. À chaque itération de l’algorithme, on met ainsi à jour les valeurs de chacun des termes des matrices ![]() et
et ![]() . Ensuite, on calcule la nouvelle valeur de la distance entre
. Ensuite, on calcule la nouvelle valeur de la distance entre ![]() et
et ![]() , et on recommence encore et encore et encore… jusqu’à ce que l’erreur totale de l’estimation reste stable. Quand c’est le cas, cela signifie que l’on a atteint la meilleure solution que l’algorithme est capable de trouver et on s’arrête. Cet algorithme n’est pas parfait — il n’y a pas de garantie théorique qu’il va réussir à trouver la meilleure solution possible — mais il a de bonnes performances dans les faits.
, et on recommence encore et encore et encore… jusqu’à ce que l’erreur totale de l’estimation reste stable. Quand c’est le cas, cela signifie que l’on a atteint la meilleure solution que l’algorithme est capable de trouver et on s’arrête. Cet algorithme n’est pas parfait — il n’y a pas de garantie théorique qu’il va réussir à trouver la meilleure solution possible — mais il a de bonnes performances dans les faits.
Le Cas du K
Reste un problème non résolu : comment choisir ![]() le nombre de signatures ? Là encore, il n’y a pas de solution exacte. Par exemple, si
le nombre de signatures ? Là encore, il n’y a pas de solution exacte. Par exemple, si ![]() = 1, la meilleure signature correspond à la signature moyenne de l’ensemble des 21 patientes. Pas pratique pour distinguer l’impact du vieillissement de celui de la cigarette. Au contraire, si l’on choisit
= 1, la meilleure signature correspond à la signature moyenne de l’ensemble des 21 patientes. Pas pratique pour distinguer l’impact du vieillissement de celui de la cigarette. Au contraire, si l’on choisit ![]() = 21 (c’est-à-dire autant de signatures que de patientes), chaque signature correspond à celle d’une patiente. Cette fois, notre estimation
= 21 (c’est-à-dire autant de signatures que de patientes), chaque signature correspond à celle d’une patiente. Cette fois, notre estimation ![]() exactement, mais on n’a rien appris sur l’impact du vieillissement. Il faut donc trouver un juste milieu. D’autant que le nombre de signatures que l’on va être capable de découvrir dépend également de la taille de nos données : plus le nombre de patientes sera important, plus on sera capable d’identifier de nombreuses signatures.
exactement, mais on n’a rien appris sur l’impact du vieillissement. Il faut donc trouver un juste milieu. D’autant que le nombre de signatures que l’on va être capable de découvrir dépend également de la taille de nos données : plus le nombre de patientes sera important, plus on sera capable d’identifier de nombreuses signatures.
Dans les faits, on cherche un compromis entre l’erreur d’estimation (la distance entre ![]() et
et ![]() ) et le niveau de compression des données, c’est-à-dire la plus petite valeur de
) et le niveau de compression des données, c’est-à-dire la plus petite valeur de ![]() qui donne une solution satisfaisante. Pour ce faire, les auteurs introduisent une mesure de la reproductibilité de leur solution. L’idée est ici d’évaluer si de faibles modifications des données ont un impact important sur les estimations. Si c’est le cas, c’est le signe que les résultats sont très sensibles aux bruits présents dans les données et que les estimations sont peu fiables. Pour évaluer cela, ils génèrent 100 matrices légèrement différentes de la matrice des données
qui donne une solution satisfaisante. Pour ce faire, les auteurs introduisent une mesure de la reproductibilité de leur solution. L’idée est ici d’évaluer si de faibles modifications des données ont un impact important sur les estimations. Si c’est le cas, c’est le signe que les résultats sont très sensibles aux bruits présents dans les données et que les estimations sont peu fiables. Pour évaluer cela, ils génèrent 100 matrices légèrement différentes de la matrice des données ![]() et estiment des solutions (
et estiment des solutions (![]() et
et ![]() ) pour chacune de ces matrices modifiées afin d’obtenir 100 matrices de signature. Ils mesurent alors la ressemblance entre toutes ces matrices de signature et calculent une valeur allant de 0 si les signatures sont très dissemblables à 1 si elles sont parfaitement similaires. Ils répètent cette procédure pour toutes les valeurs de
) pour chacune de ces matrices modifiées afin d’obtenir 100 matrices de signature. Ils mesurent alors la ressemblance entre toutes ces matrices de signature et calculent une valeur allant de 0 si les signatures sont très dissemblables à 1 si elles sont parfaitement similaires. Ils répètent cette procédure pour toutes les valeurs de ![]() (de 1 à 21), et choisissent la valeur
(de 1 à 21), et choisissent la valeur ![]() qui maximise la stabilité de la solution et minimise l’erreur d’estimation. La Figure 3 présente un exemple pour des données simulées (pour lesquelles on connaît donc la vraie solution :
qui maximise la stabilité de la solution et minimise l’erreur d’estimation. La Figure 3 présente un exemple pour des données simulées (pour lesquelles on connaît donc la vraie solution : ![]() = 10 signatures dans ce cas). Sur cet exemple, on observe que la reproductibilité est globalement très bonne jusqu’à 10 signatures, mais qu’elle diminue très rapidement pour des valeurs de
= 10 signatures dans ce cas). Sur cet exemple, on observe que la reproductibilité est globalement très bonne jusqu’à 10 signatures, mais qu’elle diminue très rapidement pour des valeurs de ![]() > 10. Inversement, l’erreur d’estimation diminue pour atteindre un minimum pour
> 10. Inversement, l’erreur d’estimation diminue pour atteindre un minimum pour ![]() = 10. En combinant ces deux critères, il est donc naturel de choisir
= 10. En combinant ces deux critères, il est donc naturel de choisir ![]() = 10, ce qui tombe bien puisque c’est également le nombre de signatures qui a été utilisé pour simuler les données !
= 10, ce qui tombe bien puisque c’est également le nombre de signatures qui a été utilisé pour simuler les données !
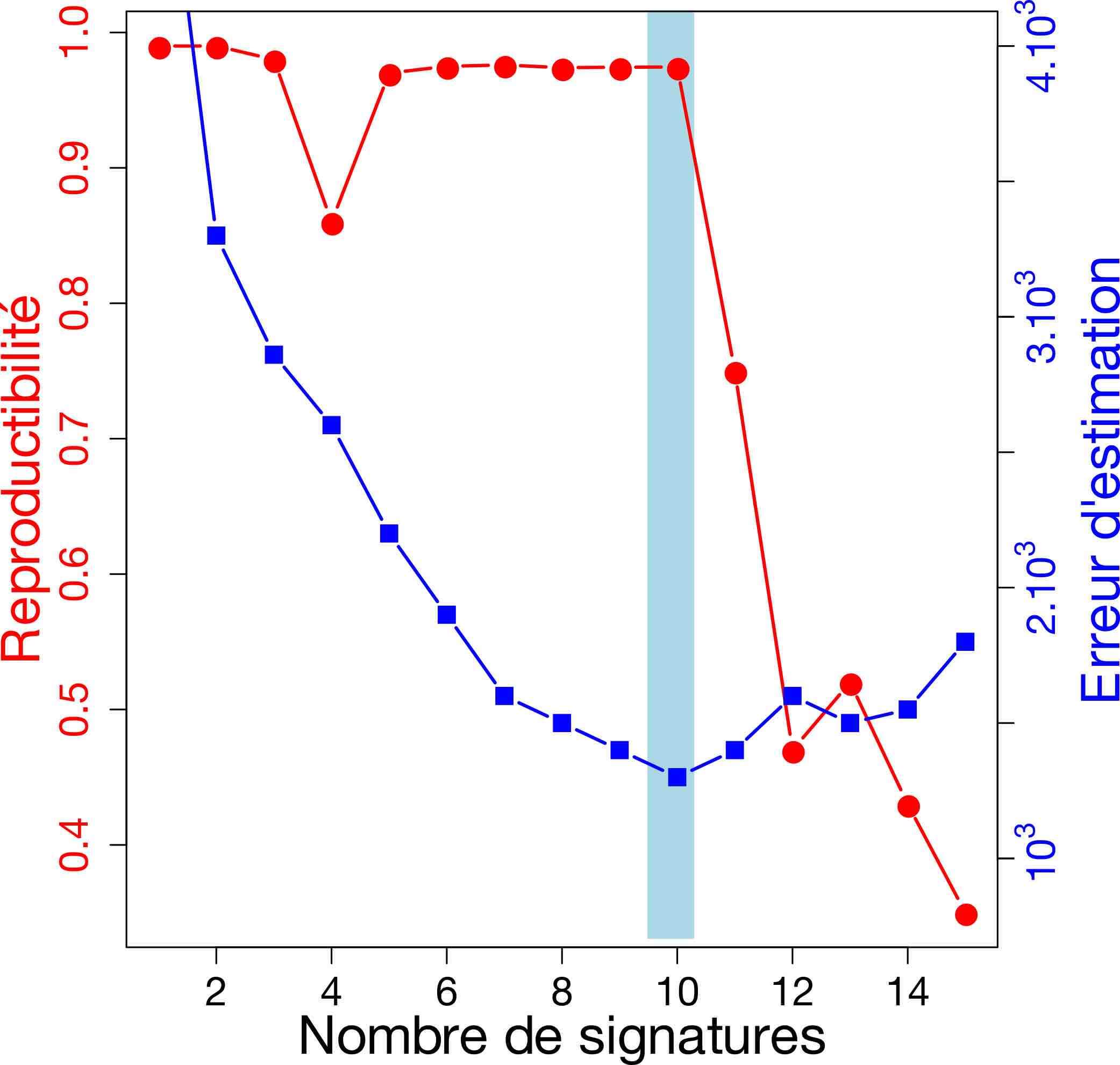
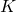 du modèle pour des données simulées. La bande bleu clair donne le vrai nombre de signatures utilisé pour la simulation.
du modèle pour des données simulées. La bande bleu clair donne le vrai nombre de signatures utilisé pour la simulation.Dans la suite de l’étude, les auteurs conduisent de nombreuses autres simulations afin de tester leur méthode, d’étudier ses limites et d’estimer sa puissance : la méthode fonctionne-t-elle quand il y a beaucoup de signatures à découvrir ? lorsque les signatures sont très similaires entre elles ? ou lorsque l’exposition aux signatures est très variable ? Ces simulations leur permettent de démontrer que leur méthode est efficace et d’en comprendre les limitations.
Retour au monde réel : applications à des vrais données
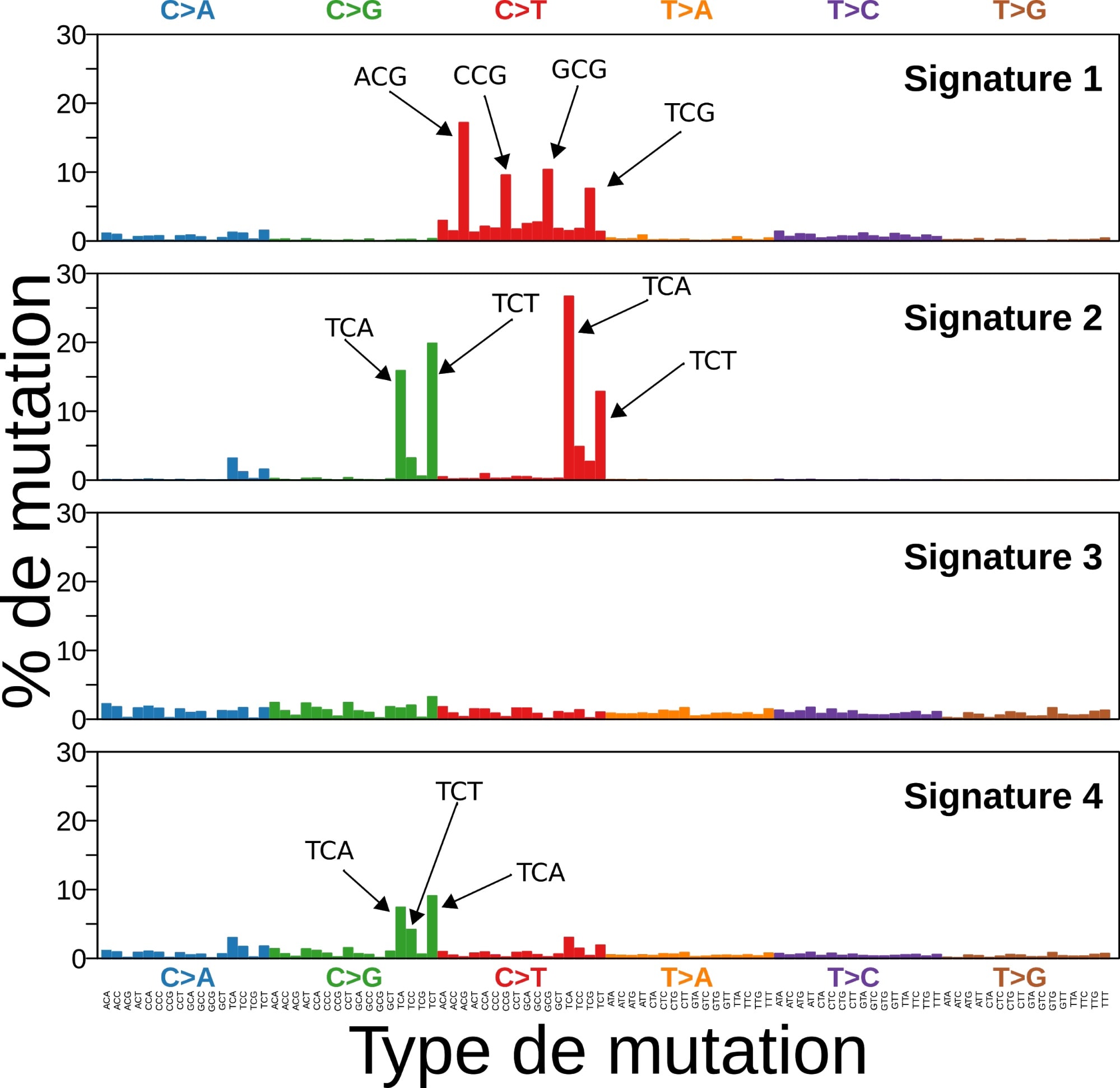
Pour finir, les auteurs utilisent cette méthode sur leur données réelles, les catalogues des 21 génomes de cancer du sein dont ils disposent. Ils découvrent ainsi quatre signatures de mutation à l’œuvre dans ces cancers (Figure 4). La signature 3 par exemple présente des taux de mutations très similaires pour tous les types de mutations, tandis que la signature 4 transforme principalement les C en G et notamment les C dont le voisin immédiat est un T. Par ailleurs, ils ont observé que la signature 4 avait une exposition particulièrement élevée chez 9 des 21 patientes. Or, ces 9 patientes avaient en commun de présenter une anomalie héréditaire dans les protéines Brca1 et Brca2, qui jouent un rôle prépondérant pour la réparation de l’ADN (voir aussi [4]). Enfin, la signature 2 est similaire à une signature de mutations observée expérimentalement dans des cellules où les gènes de la famille Apobec (des enzymes en charge de l’édition d’ARN messagers) dysfonctionnent. Ces résultats démontrent donc la puissance de cette méthode et sa capacité à découvrir des processus biologiques responsables de mutations dans les cancers.
Une matrice en pleine expansion !
En conclusion, cet article propose une nouvelle méthode d’analyse des génomes de cancer. Si, ici, ils n’ont mis en évidence que quatre signatures de mutations, de très nombreuses études complémentaires ont depuis utilisé cette méthode avec des jeux de données beaucoup plus importants [5]. La dernière en date, basée sur l’analyse de plus de 2 000 génomes de cancers, a permis de mettre en évidence 70 signatures de mutations. Toutefois, parmi ces signatures, seule la moitié est associée à des processus de mutations bien identifiés et dont les effets ont pu être validés expérimentalement. Cela souligne une des limites de cette méthode : elle permet de découvrir des candidats potentiels à l’origine des mutations, pour autant, la validation de ces candidats nécessite de conduire des expériences complémentaires difficiles.
Enfin, depuis la parution de cette méthode, on a aussi découvert qu’un certain nombre de ces signatures (par exemple la signature 1) n’étaient pas spécifiques aux génomes de cancers, et qu’on les trouvait également dans des cellules saines, ce qui souligne la grande complexité des processus de formation des cancers [6].
[*] On classe typiquement les mutations génétiques en quatre grands types : les mutations ponctuelles (1 nucléotide est remplacé par un autre), les insertions et délétions de petite taille (de 1 à 10 000 nucléotides), les insertions et délétions de grande tailles (pouvant concerner un chromosome entier) et les réarrangements (lorsque de longs fragments du génome changent de place, comme par exemple en sautant d’un chromosome à un autre). Jusqu’à récemment, on ne portait pas beaucoup d’attention aux mutations autres que les mutations ponctuelles, notamment parce que ce sont les plus faciles à identifier. Pourtant, l’impact des autres types de mutations, notamment dans les cancers, est aujourd’hui l’objet de nombreuses études.
[**] Ce problème est un cas particulier des problèmes de « réduction de dimension » qui visent à résumer l’information contenue dans des grands jeux de données avec de nombreux paramètres (les fameux big data) pour en extraire les informations les plus importantes. De très nombreuses méthodes ont été proposées pour traiter ce problème. Parmi elle, la plus utilisée est certainement l’analyse en composantes principales.
[***] Sous réserve qu’elles respectent les contraintes de positivité et que la somme de chaque colonne de ![]() soit égale à 1.
soit égale à 1.
[1] Lindblad-Toh K., et al., A high-resolution map of human evolutionary constraint using 29 mammals. Nature, 2011. DOI : 10.1038/nature10530. [Publication scientifique]
[2] Lee D. & Seung H., Learning the parts of objects by non-negative matrix factorization. Nature, 1999. DOI : 10.1038/44565. [Publication scientifique]
[3] Alexandrov L. B., et al., Mutational signatures associated with tobacco smoking in human cancer. Science, 2016. DOI : 10.1126/science.aag0299. [Publication scientifique]
[4] Nik-Zainal S., et. al., Mutational Processes Molding the Genomes of 21 Breast Cancers. Cell, 2012. DOI : 10.1016/j.cell.2012.04.024. [Publication scientifique]
[5] Alexandrov L. B., et. al., The repertoire of mutational signatures in human cancer. Nature, 2020. DOI : 10.1038/s41586-020-1943-3. [Publication scientifique]
[6] Martincorena I., et. al., High burden and pervasive positive selection of somatic mutations in normal human skin. Science, 2015. DOI : 10.1126/science.aaa6806. [Publication scientifique]