Zoom sur les sciences expérimentales

Il est difficile de catégoriser les sciences, que ce soit en leur attribuant le terme exactes, expérimentales, humaines ou sociales. Il existe en effet des différences et des nuances pour une même discipline. Pour autant, les disciplines et sous-disciplines expérimentales ont une méthodologie de recherche propre, que nous allons détailler sur cette page.

1. Importance des conditions témoins
2. Répétabilité et reproductibilité
3. Modèles d’études et modèles animaux
4. Incertitudes de mesures
5. Statistiques, hypothèses et seuil de significativité
6. Qu’est-ce qu’une méta-analyse ?

1. Importance des conditions témoins

Dans l’idéal, pour tester l’effet d’un paramètre au cours d’une expérience, seul ce paramètre doit varier. En pratique, soit on fait varier uniquement ce paramètre soit l’on s’assure, grâce à des mesures complémentaires, que seul ce paramètre est à l’origine de l’effet observé.

Par exemple, pour tester l’effet de la viscosité d’un fluide sur la vitesse de chute d’une bille d’acier dans un tube, toutes les expériences sont menées avec les mêmes conditions : une bille de même masse, de même diamètre, un tube de mêmes dimensions, etc. Ainsi, la différence observée dépendra uniquement de la viscosité du fluide. 

En sciences biologiques, on appelle condition témoin (ou contrôle) une condition expérimentale connue pour laquelle seul le paramètre testé est différent. Un témoin positif (négatif) est une condition pour laquelle le résultat est connu pour être positif (négatif). En comparant la condition test aux conditions témoins choisies, on peut conclure sur l’effet du paramètre testé. 

L’analyse d’un résultat doit toujours se faire en regard des conditions témoins. 

De manière générale, on parle d’une étude à l’aveugle lorsque l’expérimentateur ne sait pas quelles sont les conditions testées et quelles sont les conditions témoins. Lorsque les expériences sont réalisées sur des humains, une étude est à l’aveugle lorsque le participant ne sait pas de quelle condition expérimentale il fait partie. Et elle est en double aveugle lorsqu’en plus, l’expérimentateur ne sait pas quel est le groupe testé et quels sont les groupes témoins. Ainsi, l’interprétation des résultats n’est pas biaisée.

2. Répétabilité et reproductibilité

Un résultat obtenu par une expérience réalisée une seule fois ne permet pas de conclure. Elle doit être réalisée plusieurs fois dans les mêmes conditions, afin d’être sûr que le résultat observé la première fois n’est pas dû au hasard. Par exemple, une expérience ne peut pas être concluante sur une seule personne, une seule cellule ou un seul échantillon. C’est ce que l’on appelle la répétabilité d’une expérience. Elle est nécessaire pour pouvoir interpréter et publier des résultats. 

Cependant, une seule publication scientifique présentant une mesure ou une découverte ne suffit pas non plus pour qu’elle soit admise par la communauté scientifique. Encore faut-il que d’autres équipes de recherche aboutissent aux mêmes conclusions, dans les mêmes conditions et à partir du même matériel de travail : il faut que l’expérience puisse être reproduite entre les mains d’autres scientifiques. C’est la reproductibilité. Elle permet de confirmer la fiabilité scientifique et la constance des résultats obtenus.

Il faut toujours, face à un résultat scientifique, tenir compte à la fois de sa reproductibilité par d’autres équipes, mais aussi des conditions dans lesquelles il a été obtenu.

3. Modèles d’études et modèles animaux (sciences biologiques)

Les expériences peuvent se faire par des simulations par ordinateur  (in silico), sur du contenu cellulaire (ADN, protéines, etc.) (in vitro), sur des cellules vivantes maintenues dans un milieu de culture (in vitro ou in cellulo), dans des morceaux de tissus ou d’organes (ex vivo), ou directement dans des modèles animaux (vers, rats, etc.) ou humains (in vivo). Le matériel d’étude est choisi pour être le plus pertinent compte tenu de la question biologique posée. 

Les modèles animaux ne sont utilisés que lorsqu’il est nécessaire de réfléchir à l’échelle d’un organisme entier. Les protocoles des expériences sur modèles animaux et humains doivent être approuvés par un comité d’éthique.

4. Incertitudes de mesures

Toute mesure expérimentale s’accompagne d’incertitudes de mesures. Elles sont tout aussi importantes que la mesure elle-même car elles quantifient à quel point on peut avoir confiance en elle. La difficulté est de les estimer correctement.

En science de la mesure (métrologie), on distingue deux types d’incertitudes de mesure [1] :

• Les incertitudes de type A appelées incertitudes statistiques. Elles s’estiment en effectuant un grand nombre de fois la même expérience, de manière indépendante. Chaque résultat obtenu sera différent à cause des fluctuations propres à l’expérience et à l’expérimentateur. Reprenons l’exemple vu plus haut de la vitesse d’une bille d’acier tombant dans un liquide visqueux. L’expérimentateur trace deux traits sur le tube en verre et déclenche son chronomètre lorsque la bille passe le premier trait puis l’arrête lorsqu’elle passe le second. Il répète l’expérience 40 fois. Le résultat de la mesure du temps de chute sur la distance choisie va fluctuer pour deux raisons. 1) Les conditions expérimentales ne sont jamais exactement les mêmes : par exemple, la température de la pièce peut légèrement varier d’un jour à l’autre. 2) L’expérimentateur va déclencher le chronomètre avec un temps de réaction qui ne sera jamais exactement le même. Après les 40 mesures, il obtiendra une moyenne et un écart-type et pourra calculer la valeur de l’incertitude (on peut aussi utiliser la médiane et la variance).
• Les incertitudes de type B liées à l’appareil de mesurage et à l’expérimentateur peuvent être estimées sur une mesure unique. En général, elles sont évaluées à partir des données du constructeur des appareils de mesure qui ne sont pas infiniment précis. Ces incertitudes sont d’autant plus grandes que le signal reçu est faible : il est donc important de maximiser le signal reçu sur l’appareil par rapport au bruit de fond. Prenons comme exemple un voltmètre précis à 2 % mesure la tension aux bornes d’une pile AA un peu usagée. La valeur obtenue est 1,36 V. Le résultat s’écrit donc : U_pile = (1,36 ± 0,02 × 1,36) V soit (1,36 ± 0,03) V, en arrondissant. D’un autre côté, un exemple d’incertitude lié à l’expérimentateur peut être une lecture de graduations, qui ne sera jamais parfaitement précise.

Un résultat comprendra toujours les deux types d’incertitudes. S’il n’est pas possible de déterminer laquelle est prépondérante, il sera nécessaire de prendre les deux en compte. Par exemple, pour mesurer la température du centre de votre salon, vous allez utiliser un thermomètre commercial, qui possède une certaine précision — une incertitude de type B — disons de 1 %. Par ailleurs, votre salon n’est pas hermétiquement fermé et des courants d’air vont faire fluctuer la température. Pour avoir une moyenne assez précise, vous allez mesurer la température, tous les jours à la même heure, pendant 1 mois.  Vous obtenez la température de 19°C avec une incertitude de type A de 1 % également. Alors l’incertitude totale de votre résultat sera une combinaison de ces deux incertitudes (formule mathématique) qui vaudra dans ce cas 1,4 % (et non pas 2 % comme on pourrait le penser, car les incertitudes sont indépendantes).

L’incertitude de mesure est différente d’une éventuelle erreur de mesure qui peut se produire si l’expérimentateur se trompe ou que l’appareil utilisé possède un défaut de fonctionnement. 

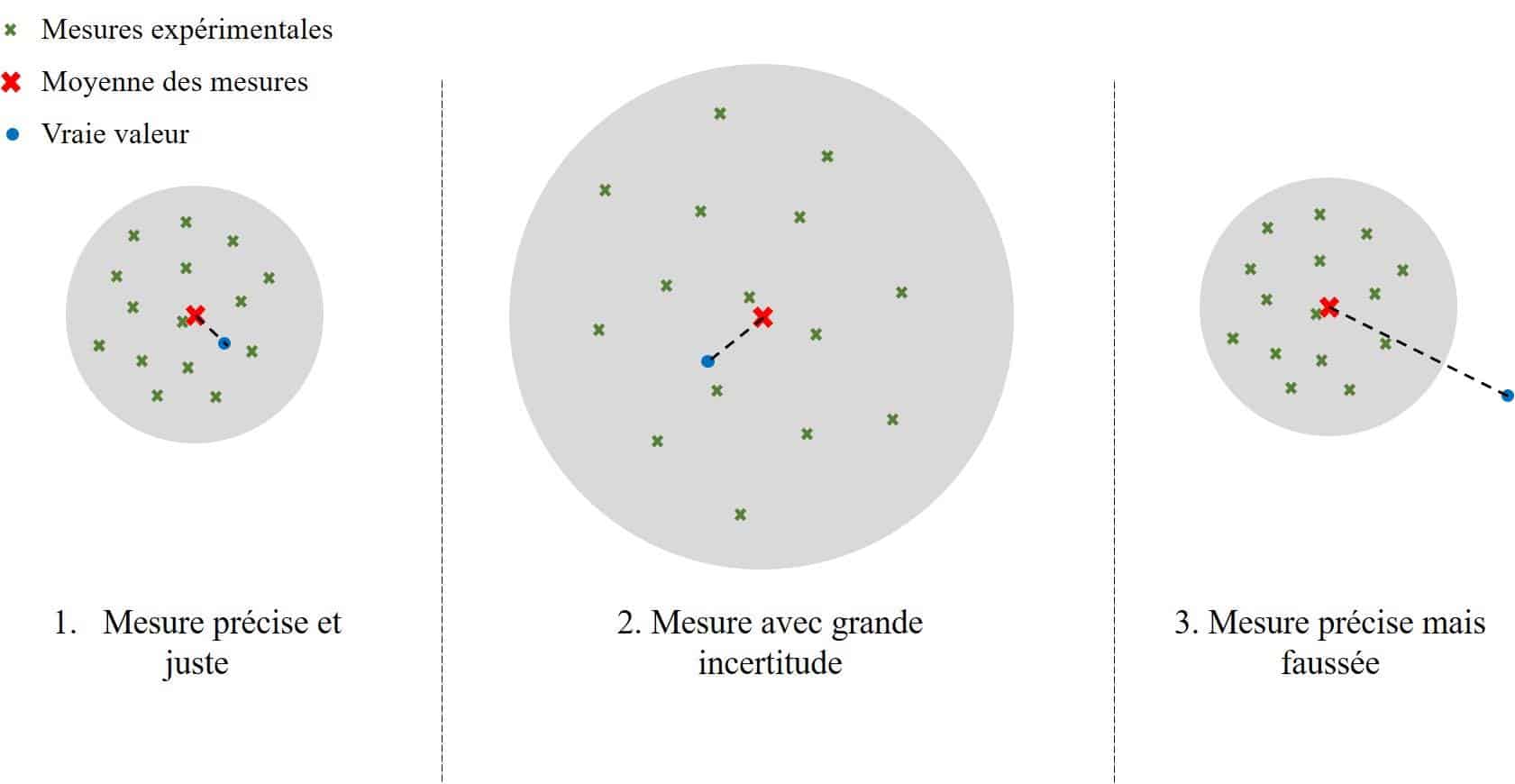
Ce schéma résume le principe des incertitudes. Voyons les mesures comme des impacts sur un mur sur lequel on vise une cible. Le point bleu représente la valeur vraie [2] de la mesure, que l’on ne connaît pas. On effectue un certain nombre de mesures (représentées par des croix vertes) ayant chacune une incertitude. On peut alors calculer la moyenne des mesures (la croix rouge) et estimer une incertitude totale (le cercle gris). La conclusion de l’expérience est que la vraie valeur se situe à l’intérieur du cercle. 

On voit sur ce schéma que 3 types de situations peuvent se présenter :

1. Les mesures effectuées sont justes et précises : le cercle d’incertitude est petit et la vraie valeur est à l’intérieur de celui-ci : c’est une bonne mesure.
2. Les mesures effectuées sont justes mais peu précises et dispersées : le cercle d’incertitude est grand mais la vraie valeur est à l’intérieur. La distance entre la moyenne et la vraie valeur est égale au cas 1, mais le cercle est bien plus grand : c’est une mesure correcte mais manquant de précision.
3. Les mesures sont précises comme dans le premier cas, mais toutes les valeurs sont éloignées de la valeur vraie à cause d’une erreur (de l’expérimentateur ou de l’appareil de mesure). La moyenne est alors éloignée de la vraie valeur et le cercle d’incertitude n’englobe pas la vraie valeur : c’est une mauvaise mesure. L’expérimentateur ne s’apercevra de cette erreur qu’après répétition de l’expérience et/ou confrontation avec la théorie. 

Le choix et l’estimation des incertitudes de mesure est un travail à part entière que chercheuses et chercheurs s’efforcent de faire pour que leurs mesures quantitatives soient interprétées correctement.

5. Statistiques, hypothèses et seuil de significativité

Quelle que soit la discipline expérimentale, pour que des résultats soient considérés comme scientifiquement robustes et puissent être publiés, ils sont soumis à des tests statistiques. Ces tests comparent les résultats et incertitudes de mesures à ce qui serait obtenu uniquement grâce au hasard ou avec d’autres conditions expérimentales.

Approche utilisée

Actuellement, la majorité des études expérimentales utilise l’approche statistique fréquentiste. Elle cherche à calculer la probabilité qu’un événement se produise, en connaissant l’hypothèse de travail. Ensuite, cette probabilité est comparée à un seuil préétabli, qui délimite à partir de quelle probabilité le résultat est considéré « extraordinaire ».

Par exemple, imaginons que l’on s’intéresse à l’influence de la couleur des yeux sur la taille d’une population. Avant de procéder à l’expérience, on va énoncer une hypothèse au sujet du paramètre à étudier, c’est l’hypothèse nulle (H0). Ici, on pose comme hypothèse nulle le fait que quelle que soit la couleur des yeux, les personnes sont de même taille. Si l’hypothèse nulle n’est pas rejetée par les statistiques, on conclura donc qu’il n’y a pas de différence de taille entre les personnes en fonction de la couleur des yeux.

On émet ensuite une hypothèse alternative qui, dans ce cas, peut prendre trois formes :

1. les personnes aux yeux bleus ont une taille différente que celles aux yeux marrons (H1) ;
2. les personnes aux yeux bleus sont plus grandes que celles aux yeux marrons (H2) ;
3. les personnes aux yeux bleus sont plus petites que celles aux yeux marrons (H3).

L’hypothèse alternative se pose obligatoirement avant l’expérience. Sinon, il y a un risque important de fausser les conclusions en posant des hypothèses a posteriori, c’est-à-dire en ayant déjà un aperçu des résultats. Pour aller plus loin sur la question, vous pouvez visionner cette vidéo de la chaîne de Christophe Michel Hygiène Mentale.

La puissance d’un test statistique est la probabilité qu’il détecte une différence entre les conditions. Elle dépend de plusieurs paramètres comme la taille, la nature de l’échantillon ou le test en lui-même.

Une fois le test choisi, il permet de tester la valeur p, c’est-à-dire la probabilité, si H0 est vraie, que la différence observée entre la taille des personnes aux yeux bleus et celle des personnes aux yeux marrons est uniquement due au hasard. Cette valeur p est plus connue sous son nom anglais de p-value. 

Le seuil préétabli s’appelle le seuil de significativité. Il représente le risque de rejeter H0 alors qu’elle est vraie. C’est donc le risque, toléré, que la conclusion soit fausse. Ce seuil est fixé arbitrairement avant de réaliser le test statistique.

Exemple

On cherche ici à tester l’hypothèse H2 (les personnes aux yeux bleus sont plus grandes que celles aux yeux marrons) avec un seuil de significativité de 5 %. Après avoir calculé les tailles des personnes dans les deux échantillons, on utilise un test statistique qui calcule la probabilité que cette différence soit due au hasard, avec un risque d’erreur toléré de 5 % soit 0,05.

• Si p ≥ 0,05, il y a plus de 95 % de chance de rejeter H0 alors qu’elle est vraie. On ne rejette donc pas H0 : il n’y a pas de différence de taille.
• Si p < 0,05, il y a moins de 5 % de chance de rejeter H0 alors qu’elle est vraie. On rejette donc H0 et on accepte H2 : les personnes aux yeux bleus sont plus grandes.

Admettons que p = 0,02. On conclut alors que les personnes aux yeux bleus sont plus grandes que les personnes aux yeux marrons avec un risque d’erreur de 2 %. On a 2 % de chance de se tromper en faisant cette conclusion. 

Difficile interprétation de la valeur p

Attention à bien interpréter la valeur p : c’est la probabilité de rejeter H0 alors qu’elle est vraie. Ce n’est pas la probabilité que H0 soit vraie ! Un résultat n’est ainsi jamais vrai ou faux. Il est considéré statistiquement validé si la probabilité de rejeter l’hypothèse nulle par erreur est inférieure au seuil de significativité choisi. Ce critère est arbitraire et repose uniquement sur les statistiques. Il arrive qu’une hypothèse de travail soit rejetée alors qu’elle est pourtant valide : c’est un faux négatif. Il se peut également qu’une différence statistiquement significative (valeur p < seuil) ne soit pour autant qu’un faux positif. De même que pour les incertitudes de mesures, cela montre l’importance de répéter et de reproduire les expériences, et de comprendre finement l’utilisation des tests statistiques appliqués.

Un résultat statistiquement significatif ne signifie pas non plus que l’effet observé est nécessairement important en termes d’amplitude. Par exemple, le test statistique choisi indique ici que les personnes aux yeux bleus sont plus grandes que les personnes aux yeux marrons. Cela ne veut pas dire que les personnes aux yeux bleus sont  — beaucoup — plus grandes. La différence peut n’être que de 1 mm.

L’utilisation massive, et comprise souvent partiellement, de cette valeur p comme unique critère attestant de l’importance d’un résultat est vivement critiquée par les statisticiennes et statisticiens de métier et de plus en plus par l’ensemble de la communauté scientifique. Ce serait notamment une des raisons expliquant le manque de reproductibilité des travaux dans le domaine biomédical. Nous abordons ce point dans les critiques du système actuel de publication. Pour aller plus loin, vous pouvez également visionner cette vidéo de la chaîne de Lê Nguyên Hoang Science4All.

Alternative possible

Une autre approche statistique peut être utilisée pour tester des résultats scientifiques : l’approche bayésienne. La démarche est inversée par rapport à l’approche fréquentiste. Les fréquentistes testent la probabilité d’une observation, connaissant l’hypothèse de départ : cela calcule donc la vraisemblance de l’observation, compte tenu d’une hypothèse. L’approche bayésienne, au contraire, teste la probabilité qu’une hypothèse soit valide, compte tenu d’une observation. Elle calcule la plausibilité de l’hypothèse.

On part de la probabilité d’une hypothèse a priori. Elle ne représente pas la réalité, mais notre préjugé sur la question posée. Ensuite, on procède à une expérience. Au lieu de calculer la probabilité que le résultat soit ou non dû au hasard, on calcule plutôt la probabilité que l’hypothèse soit vraie, connaissant le résultat de l’expérience. Si le résultat obtenu est très surprenant au regard de l’hypothèse posée a priori, la probabilité sera faible, elle tendra vers 0. Dans ce cas, la plausibilité de l’hypothèse diminue, nous permettant de la mettre à jour. Cette deuxième hypothèse va alors servir d’hypothèse a priori pour l’expérience suivante, et ainsi de suite. À force de répéter l’expérience, la probabilité obtenue à chaque fois permet d’affiner l’hypothèse petit à petit, au fur et à mesure. D’où le nom d’inférence bayésienne. Plus la probabilité de l’hypothèse sera proche de 1, plus on pourra considérer qu’elle est « vraie ».

Pour comprendre en détails comment fonctionne l’inférence bayésienne et l’intérêt qu’elle peut avoir en recherche scientifique, nous vous conseillons :

• la vidéo très didactique La pensée bayésienne d’Hygiène Mentale ;
• la série de vidéos sur le bayésianisme, plus poussées, de Science4All.

6. Qu’est-ce qu’une méta-analyse ?

Il arrive que la communauté scientifique ne puisse conclure sur une question donnée. Elle pourra alors essayer de compiler des résultats antérieurs et analyser si une tendance se dégage. Prenons l’exemple de scientifiques qui n’arrivent à connaître les effets d’un traitement médical parce que les publications présentent des résultats contradictoires ou non-concluants. En compilant l’ensemble des données de ces études, il leur sera peut-être possible d’aboutir à une conclusion scientifique, par le procédé appelé méta-analyse. 

Pour cela, les scientifiques vont d’abord choisir les paramètres qu’ils vont utiliser pour décider s’ils prennent en compte une étude ou non. Autrement dit, ils devront définir des critères d’inclusion. En premier lieu, il s’agit de répertorier toutes les études qui traitent de la question, et que les scientifiques vont juger rigoureuses (protocole détaillé, tests statistiques expliqués, etc.) et suffisamment proches pour être compilées. Ensuite, il peut y avoir d’autres critères fixant par exemple un nombre minimal de données.

Lorsque les critères d’inclusion sont définis et que toutes les études qui les remplissent sont rassemblées, l’équipe va analyser l’ensemble des données, les compiler puis réaliser des tests statistiques afin d’observer si leur hypothèse alternative est acceptée ou non. 

En sciences biologiques, comment est-il possible d’observer l’effet du traitement médical de manière robuste à partir de résultats qui, pris séparément, ne permettent pas de conclure ? Nous avons vu que la capacité d’un test statistique à détecter une différence dépend de sa puissance. Or la puissance est fortement liée à la taille de l’échantillon étudié. En compilant les données issues de plusieurs études — qui ne se recoupent pas — on augmente alors la puissance des statistiques utilisées, et donc la probabilité de détecter une différence existante.

Ainsi, alors que conclure peut ne pas être possible sur un échantillon de taille moyenne, une méta-analyse peut permettre de connaître l’effet d’un paramètre sur une plus grande population. Pour autant, une méta-analyse reste basée sur une méthodologie, des hypothèses, des critères d’inclusion et des tests statistiques propres, qu’il faut prendre en considération.

---

[1] Mesure et incertitudes, par Éduscol

[2] En métrologie, la « valeur vraie » d’une grandeur de référence est « sa valeur considérée comme unique et, en pratique, impossible à connaître ». D’après Wikipédia (consulté en janvier 2019).

---

Texte et images, à l’exception des images soumises à droits d’auteurs différents : voir au cas par cas en légende.