Chargement de l'article...
Écriture : Pauline Bennet
Relecture scientifique : Élisa Ruiz
Relecture de forme : Éléa Héberlé et Eléonore Pérès
Temps de lecture : environ 9 minutes.
Thématiques : Photonique (Physique)
Publication originale : Gondarenko A., et al., Spontaneous Emergence of Periodic Patterns in a Biologically Inspired Simulation of Photonic Structures. Physical Review Letters, 2006. DOI : 10.1103/PhysRevLett.96.143904.

Si la lumière peut nous intriguer et nous captiver, voire même nous faire rêver, les physiciens cherchent depuis des années à la contrôler. Utilisée pour transporter de l’information, convertie pour devenir de l’électricité ou encore manipulée pour rendre des objets presque invisibles, la lumière est en effet de mieux en mieux comprise et utilisée pour répondre à des besoins technologiques précis. En 2006, Gondarenko et ses collègues utilisent une méthode numérique d’optimisation, inspirée de l’évolution biologique des populations, pour rechercher un composant optique permettant de concentrer la lumière dans un espace très restreint.
Les structures photoniques
Vous aussi vous aimez jouer avec votre chat ? Moi, j’adore jouer avec le mien et un pointeur laser, grâce auquel je réussis à faire perdre du poids à mon monstre de compagnie tout en m’obligeant à faire du tri dans mes affaires. Tout ce qui tombe et qui casse lors des poursuites chat-laser finit à la poubelle et libère de l’espace dans mon salon. Si je vous parle de cela, c’est parce qu’un pointeur laser est un composant qui génère de la lumière et la ré-expédie dans une direction unique et limitée dans l’espace : la lumière est focalisée. Cet innocent objet qui focalise la lumière dans une direction particulière (et qui permet à mon chat de détruire ma maison) est ce que l’on appelle dans le jargon une structure photonique.
Une structure photonique est un assemblage de matière qui permet de contrôler la lumière : la diriger dans une direction particulière, la transporter, la convertir en électricité, etc. Le mot photonique vient de « photon », et un photon est une représentation de ce qui constitue la lumière. Si quelque chose est qualifié de « photonique », c’est donc qu’il est en rapport avec de la lumière. La fibre optique et les cellules photovoltaïques sont deux autres exemples de ce que peuvent être des structures photoniques qui nous sont utiles dans la vie de tous les jours. La fibre optique est une sorte de tuyau qui permet de transporter la lumière. Cette lumière contient de l’information (grâce à la science informatique, même si c’est tellement incroyable qu’on pourrait croire à de la magie), et cette information est guidée le long de la fibre optique. Si vous n’êtes pas encore convaincus que les structures photoniques sont essentielles à notre mode de vie, parlons un peu des cellules photovoltaïques qui composent nos panneaux solaires. Ces structures photoniques ont pour rôle de transformer la lumière du Soleil en électricité. Elles s’occupent de récupérer la lumière du soleil, et une fois qu’elles ont absorbé cette lumière, elles la convertissent en énergie que nous utilisons pour éclairer nos maisons lors des froides journées d’hiver.
La focalisation de la lumière
En 2006, Gondarenko et son équipe de recherche décrivent dans une publication scientifique une structure photonique qui focalise la lumière, c’est-à-dire qui concentre la lumière dans un tout petit endroit de la structure. Mais en plus de concentrer la lumière, cette structure photonique l’amplifie de près de 40 fois. Imaginez que vous placiez des moutons dans un pré et que vous vous retrouviez un peu après avec la majorité de ces moutons, devenus bien plus gros, dans une petite grange au milieu du pré ! Dans cette analogie, les moutons représentent la lumière (un mouton individuel étant un photon), la structure photonique c’est tout le pré, et la grange représente l’endroit où la lumière sera focalisée. Les physiciens ne cherchent pas de la laine sur la lumière, c’est l’énergie contenue dans cette lumière qui les intéresse. 40 fois plus de lumière, c’est 40 fois plus d’énergie. Et comme cette énergie est concentrée dans un espace réduit, elle devient plus facile à exploiter.
Vous pouvez observer une représentation de la structure trouvée par Gondarenko et ses collègues sur la Figure 1. Il s’agit d’une structure composée de deux matériaux différents, l’un représenté en noir et l’autre en bleu. On peut diviser la structure en deux parties : la partie supérieure et la partie inférieure. Chacune de ces parties est ce qu’on appelle un miroir de Bragg qui réfléchit la lumière, c’est-à-dire qui la renvoie vers là d’où elle vient, un peu comme si la lumière était un mouton et le miroir de Bragg une paroi. Lorsque le mouton arrive devant la paroi, il n’a plus d’autre choix que de faire demi-tour. Puisque la lumière, au centre, est réfléchie par les deux miroirs qui l’entourent dessus et dessous, elle est piégée entre ces deux miroirs, elle ne peut pas s’échapper. Imaginez qu’au niveau des parois de la grange, le mouton accède à de la nourriture. À chaque fois qu’il atteint une paroi, il mange, donc il grossit, avant de faire demi tour et de rencontrer une autre paroi. Après plusieurs allers-retours, on se retrouve avec un plus gros mouton, qui reste dans la petite grange au lieu de se promener dans tout le pré — ou avec davantage de lumière au centre de la structure photonique.

Comment les chercheurs ont-ils trouvé la structure ?
L’optimisation numérique
L’optimisation est un processus qui consiste à trouver la solution la plus efficace pour atteindre un objectif, parfois en respectant des contraintes spécifiques. Si l’on prend l’exemple d’un trajet à effectuer, d’un point de départ A à un point d’arrivée B, l’objectif est d’arriver au point B. Optimiser ce trajet consiste à chercher le chemin le plus court pour l’effectuer, ou bien le chemin le moins cher, ou encore celui qui nous fait consommer le moins d’énergie. En fonction des paramètres (le temps imposé, le prix, etc.) fixés, la solution choisie n’est pas la même : si le but est d’arriver le plus vite possible au point B, la solution est de passer par l’autoroute ; mais pour arriver en ayant dépensé le moins d’argent possible, cette autoroute à péage sera à éviter.
Gondarenko et son équipe ont utilisé un algorithme d’optimisation, c’est-à-dire une suite d’instructions données à un ordinateur dans le but de trouver une structure photonique capable de focaliser la lumière. La structure photonique — le pré avec sa grange — est alors l’équivalent du trajet de A vers B, c’est ce que les auteurs de la publication cherchent à optimiser. Le point d’arrivée B, l’objectif, est la focalisation de la lumière au sein de la structure : avoir des gros moutons dans la grange plutôt que des petits moutons éparpillés dans tout le pré. Quelle taille donner au pré ? Quelle taille et quelle forme donner à la grange ? Où doit-elle être placée dans le pré, sur un bord ou au centre ? C’est l’algorithme d’optimisation qui permet de chercher la meilleure solution.
L’algorithme utilisé par les chercheurs
L’algorithme qu’ont choisi d’utiliser les chercheurs est inspiré de l’évolution biologique des populations. Dans le cas de l’évolution biologique, les populations d’individus peuvent varier au cours des générations grâce à la sélection naturelle, aux croisements, aux mutations. Ces évènements aléatoires permettent de conduire à des individus qui présentent des caractéristiques légèrement différentes, tout en restant proches de celles des individus dont ils sont issus. De la même façon, l’algorithme d’optimisation crée une population initiale de structures photoniques : vous voilà avec plein de prés et de granges, de différentes tailles et de différentes formes. En mélangeant les caractéristiques des meilleurs prés — ceux dans lesquels on a les plus gros moutons dans la grange — les chercheurs obtiennent des prés de plus en plus performants, qui viennent remplacer les prés les moins efficaces. L’algorithme d’optimisation a été utilisé plusieurs fois par Gondarenko et ses collègues et à chaque fois la même structure-solution a été proposée : celle que nous avons décrite plus haut (Figure 1).
Des modèles physiques pour comprendre la nature
Étudier la physique, c’est étudier l’art de décrire la nature, et pour être capable de bien la décrire, il faut d’abord l’avoir comprise. Pour pouvoir dire qu’il a compris un phénomène physique, il faut que le physicien soit capable d’expliquer les phénomènes qu’il observe (pourquoi une balle tombe-t-elle lorsqu’on la lâche ?), mais il faut aussi qu’il prédise ce qu’il va se passer (si on lance un ballon dans une direction particulière, où va-t-il retomber ?). Si ces deux éléments, la compréhension et la prédiction, sont au rendez-vous, le physicien dispose alors de ce qu’on appelle un modèle physique. Plus les systèmes physiques étudiés sont simples, c’est-à-dire constitués de peu de matériaux par exemple, plus il est facile d’établir des modèles pour représenter ces systèmes.
Ce qui est remarquable dans les travaux de Gondarenko et son équipe, c’est que la structure photonique trouvée par l’algorithme est périodique : elle contient un motif — une période — qui se répète. Une semaine est une période. L’année, constituée d’une suite de plusieurs semaines, est donc périodique. Dans la structure photonique qui nous intéresse, la période correspond à deux couches (une bleue et une noire) du miroir de Bragg. Comme nous avons deux miroirs, contenant chacun plus de deux couches, la structure est bien périodique. Or, la périodicité est une caractéristique de la simplicité, puisqu’au lieu d’avoir toute une grosse structure à étudier, on peut alors se contenter d’étudier une période de la structure pour comprendre son fonctionnement global. Le fait qu’un algorithme d’optimisation propose une structure périodique comme solution suggère donc qu’il n’est pas nécessaire d’imaginer des structures à la géométrie très complexe pour que celles-ci soient efficaces, et que les structures les plus simples sont peut-être finalement les meilleures ! Pourquoi se compliquer la vie quand on peut faire simple ?

Écriture : Pauline Bennet
Relecture scientifique : Élisa Ruiz
Relecture de forme : Éléa Héberlé et Eléonore Pérès
Temps de lecture : environ 14 minutes.
Thématiques : Photonique (Physique)
Publication originale : Gondarenko A., et al., Spontaneous Emergence of Periodic Patterns in a Biologically Inspired Simulation of Photonic Structures. Physical Review Letters, 2006. DOI : 10.1103/PhysRevLett.96.143904.

Si la lumière peut nous intriguer et nous captiver, voire même nous faire rêver, les physiciens cherchent depuis des années à la contrôler. Utilisée pour transporter de l’information, convertie pour devenir de l’électricité ou encore manipulée pour rendre des objets presque invisibles, la lumière est en effet de mieux en mieux comprise et utilisée pour répondre à des besoins technologiques précis. En 2006, Gondarenko et ses collègues utilisent une méthode numérique d’optimisation, inspirée de l’évolution biologique des populations, pour rechercher un composant optique permettant de concentrer la lumière dans un espace très restreint.
Contrôler la lumière, un enjeu de recherche
Un des défis de la physique du XXIe siècle est d’apprendre à manipuler les ondes électromagnétiques, dont les ondes lumineuses, pour répondre à des besoins technologiques précis. La compréhension de l’interaction entre la lumière et la matière nous permet de concevoir des composants de matière capables de modifier des ondes électromagnétiques de façon suffisamment contrôlée pour être utilisées dans des systèmes technologiques variés. On appelle ces composants des structures photoniques. Par exemple, les fibres optiques permettent de guider l’information que transporte une onde électromagnétique très rapidement d’un endroit à un autre. Les cellules photovoltaïques, quant à elles, convertissent la lumière du Soleil en électricité. Et ces deux exemples ne sont qu’une petite fraction de tous les types de structures photoniques existantes !
Une structure photonique focalisant la lumière
Gondarenko et ses collègues ont publié en 2006 une publication dans laquelle ils décrivent comment ils ont optimisé une structure photonique pour qu’elle puisse focaliser la lumière. Cela signifie qu’ils ont essayé de faire en sorte qu’une intensité très forte de lumière soit concentrée dans un espace très restreint de la structure. Pour évaluer l’efficacité d’une structure, les chercheurs envoient une onde électromagnétique sur celle-ci puis calculent son intensité partout dans la structure. Ils vérifient ensuite qu’une très importante intensité lumineuse est contenue dans seulement une petite partie de la structure, alors que partout ailleurs cette intensité lumineuse est négligeable.
L’efficacité d’une structure peut se traduire à l’aide d’une fonction mathématique, qu’on appelle une fonction de mérite. Cette fonction représente la similitude entre l’objectif (la focalisation de l’onde dans la structure) que l’on cherche à avoir dans un cas idéal et ce qu’une structure donnée permet d’obtenir. Cela signifie que plus la valeur de la fonction de mérite est grande, plus la réponse optique de la structure photonique est proche de l’objectif désiré, donc plus la structure est efficace.
La structure optimisée par l’équipe de Gondarenko permet d’augmenter l’intensité d’un champ électromagnétique au centre de la structure d’environ 40 fois par rapport à l’intensité du champ initial. C’est donc une réussite, la lumière est focalisée au sein de la structure.
Les contraintes d’optimisation
Il peut exister des structures photoniques de différentes formes et de différentes tailles. Le nombre et le choix des matériaux utilisés pour fabriquer la structure photonique, ainsi que la forme géométrique (couches planaires, cylindres, etc.) donnée à ces matériaux, constituent des contraintes d’optimisation. Plus les contraintes sont fortes, moins l’algorithme d’optimisation a la liberté de concevoir des structures variées. En contrepartie, l’ajout de contraintes d’optimisation permet de s’assurer que les structures sont fabricables avec la technologie dont nous disposons.
Pour différencier des matériaux, on peut utiliser la notion d’indice de réfraction. En fonction de la valeur de cet indice, la lumière n’a pas le même comportement lorsqu’elle rencontre le matériau. Le choix des matériaux se fait donc en fonction de la valeur de leur indice de réfraction, pour pouvoir « jouer » sur le comportement de la lumière, dans ce cas particulier sur sa focalisation.
Gondarenko et ses collègues ont choisi de limiter leur recherche à des composants d’une forme rectangulaire, n’utilisant au total que deux matériaux distincts, et donc que deux indices de réfraction différents. Ce choix semble pertinent car la performance de composants alternant deux matériaux n’est plus à démontrer. En effet, les filtres optiques, des composants utilisés pour réfléchir ou pour transmettre une partie spécifique du spectre électromagnétique, sont très souvent constitués de couches pleines alternant deux matériaux comme représenté sur la Figure 1, ce qu’on appelle des structures multicouches [1].

Gondarenko et ses collègues ont cherché une structure qui réponde à moins de contraintes géométriques que les structures multicouches, en imaginant des structures dont chaque couche pourrait être constituée non pas par un seul, mais par deux matériaux. Pour cela, ils divisent leur structure photonique rectangulaire de base en 90 cases, chacune ayant une taille de 20 nm par 20 nm. Ainsi, nous pouvons nous représenter leur structure-type comme étant un damier plutôt qu’un mille-feuille, comme illustré sur la Figure 2.
Ce que les méthodes numériques apportent
En utilisant l’informatique, les physiciens simulent numériquement les systèmes physiques qu’ils étudient, permettant ainsi de bien plus nombreuses expérimentations, un gain de temps considérable ainsi que des avancées dans notre compréhension de la physique. En effet, il faut s’assurer que la simulation d’un système physique permet d’obtenir les mêmes phénomènes que le système physique réel. Si ce n’est pas le cas, c’est que le modèle utilisé pour simuler le système étudié ne représente pas suffisamment la réalité, ce qui est le témoin d’un manque de compréhension du système physique étudié.
Si la simulation permet de recréer avec un ordinateur des systèmes physiques déjà connus, l’optimisation numérique permet d’automatiser la recherche de nouveaux systèmes physiques. Il existe de nombreuses variétés d’algorithmes d’optimisation, certains se basant uniquement sur des considérations mathématiques et d’autres s’inspirant de mécanismes observés dans la nature, comme l’évolution d’une population [2], la recherche de nourriture chez les fourmis [3], ou encore le déplacement par essaim de certains oiseaux [4].
L’algorithme d’optimisation choisi
Pour rechercher la meilleure structure photonique permettant de focaliser la lumière, l’équipe de recherche a choisi d’utiliser un algorithme d’optimisation inspiré de la reproduction sexuée d’une population. L’idée est qu’à partir d’une population de structures photoniques initiales, des mécanismes inspirés de l’évolution biologique et de la sélection naturelle permettent de créer de nouvelles structures photoniques qui soient de plus en plus efficaces. Les chercheurs ont alors démarré le procédé d’optimisation en partant d’une population constituée de 180 structures photoniques complètement aléatoires : c’est-à-dire que chacune des 90 cases de chaque structure a une chance sur deux d’être remplie par l’un ou l’autre des matériaux. Ensuite, les chercheurs testent chaque structure et évaluent le degré de focalisation de la lumière. Ils les classent selon ce degré, de la moins efficace à celle qui permet la meilleure focalisation.
Plusieurs procédés d’évolution biologique — sélection, croisement, mutation — sont ensuite utilisés pour converger vers une structure-solution qui soit la plus efficace possible :
- La sélection consiste à choisir les structures qui vont disparaître de la population en étant remplacées par de nouvelles. Gondarenko et son équipe ont choisi de remplacer les 40 % les moins efficaces de leurs structures par de nouvelles structures afin de limiter la transmission des configurations les moins optimales.
- Pour créer les nouvelles structures, le procédé de croisement permet de mélanger deux structures existantes pour en former une nouvelle. Les chercheurs ont décidé d’effectuer des croisements uniquement entre les 40 % des meilleures structures.
- Enfin, le procédé de mutation altère la structure nouvellement créée par le croisement : chaque case de chacune des structures se voit changer de matériau qui la compose avec une probabilité qu’ils ont arbitrairement fixée à 0,1 %. Cette étape est importante pour la découverte de nouvelles structures dans la population.
Cela signifie que 60 % de la population est inchangée après une génération (une itération) alors que les 40 % restant, représentant les structures les moins efficaces, sont remplacées par les structures générées grâce aux étapes (1) et (3) du procédé évolutionnaire (Figure 3). Les chercheurs laissent la population « évoluer » sur 5 000 générations.
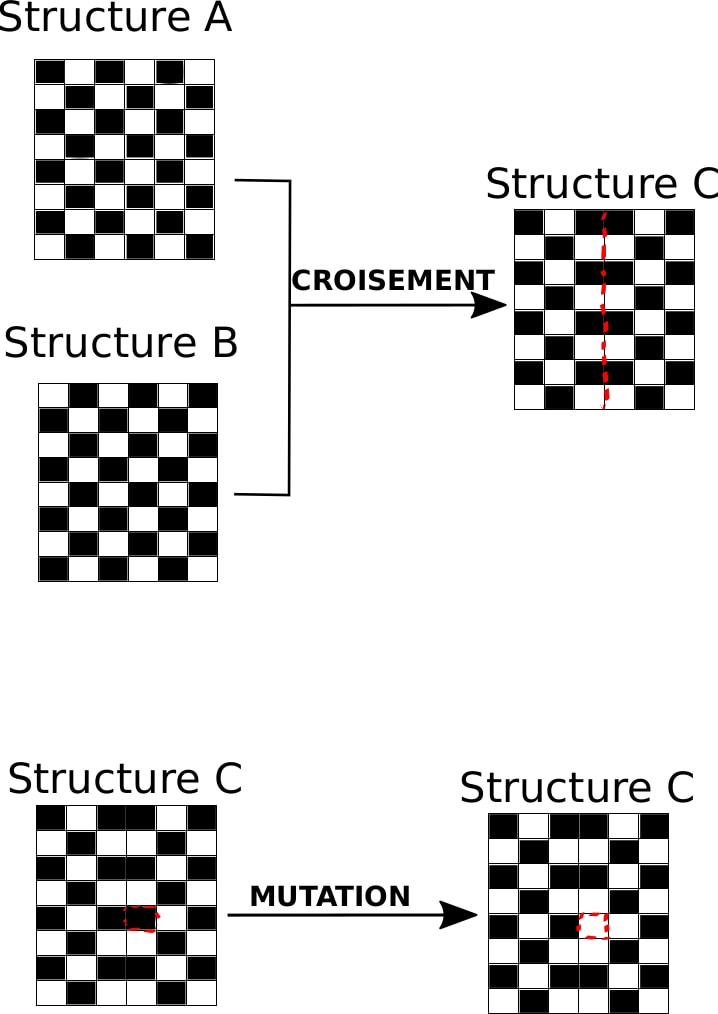
Figure 3. Schéma représentant les procédés de croisement et de mutation de l’algorithme évolutionnaire. Le détail du procédé de croisement n’étant pas explicité dans la publication originale, le croisement est ici une modélisation probablement inexacte du réel procédé utilisé par les auteurs. Dans cet exemple, les structures A et B sont des opposés : chaque case blanche de A est noire en B et inversement. Après croisement, la structure « fille » C possède la partie gauche de A et la partie droite de B, ses deux structures « parentes ». La structure C subit ensuite une mutation sur l’une de ses cases (entourée de pointillés rouges) qui passe de noire à blanche.
La structure-solution trouvée
La Figure 4 représente la meilleure structure photonique obtenue dans la population au cours de quatre étapes d’une optimisation.
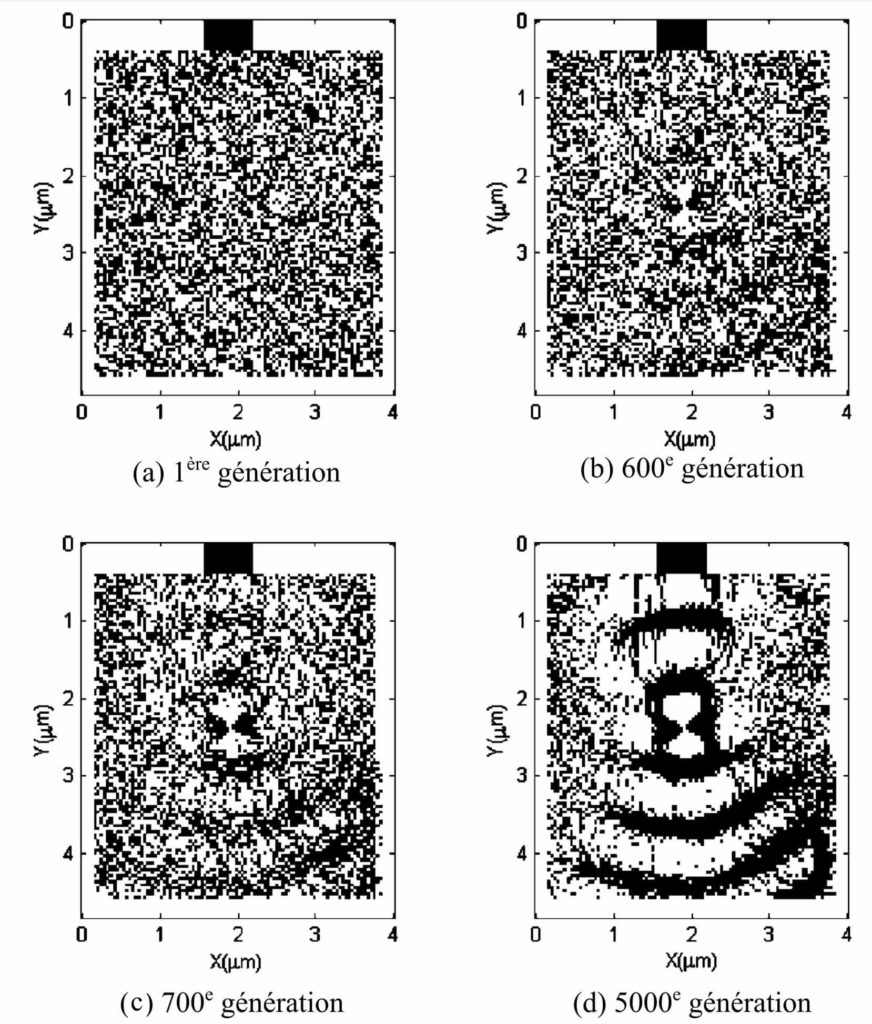
Dans cette image, les zones blanches ne représentent pas une absence de matériaux, mais celui des deux dont l’indice de réfraction est le plus faible, alors que les zones noires témoignent une présence du matériau dont l’indice de réfraction est le plus fort. Aucune case ne peut être vide. En haut à gauche (1ère génération), il s’agit de la meilleure structure initialement présente dans la population. Cette structure est non-ordonnée, puisque la répartition des matériaux dans les cases est effectuée par un procédé aléatoire. En haut à droite, il s’agit de la meilleure structure de la population après son évolution sur 600 générations. On peut déjà commencer à apercevoir des zones de concentration des matériaux, en regardant le centre de la structure. En bas à gauche, il s’agit de la structure la plus efficace après 700 générations. L’organisation de la matière se précise un peu plus, nous voyons plus nettement une répartition de zones claires et de zones sombres. Finalement, l’évolution aboutit à la structure-solution représentée en bas à droite de la figure, après 5 000 générations. Un motif bien net est visible, avec le matériau représenté en noir qui laisse deviner un huit au centre de la structure, puis des demi-cercles qui s’agrandissent en s’éloignant du centre de la structure.
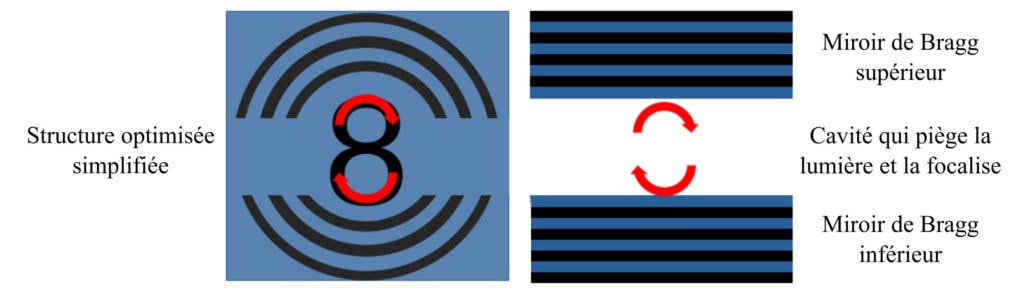
Gondarenko et ses collègues ont ensuite tenté de comprendre pourquoi cette structure permet de focaliser efficacement la lumière. Ils ont identifié dans la structure-solution deux structures dites miroir de Bragg (Figure 5). Un miroir de Bragg est une structure bien connue des physiciens car elle consiste en une multicouche alternant deux matériaux dont les épaisseurs sont spécifiquement conçues pour réfléchir complètement la lumière. La structure proposée comme solution par l’algorithme évolutionnaire de Gondarenko et ses collègues ressemble beaucoup à deux miroirs de Bragg qui partent du centre de la structure mais, au lieu de présenter des couches planaires, les couches sont demi-circulaires. Cette particularité n’empêche en rien la bonne réflexion de la lumière sur les deux miroirs de Bragg déformés, donc la lumière au centre de la structure va se réfléchir sur la paroi du bas du miroir de Bragg supérieur, puis sur la paroi du haut du miroir de Bragg inférieur. Ainsi, une sorte de cavité est formée au centre de la structure dans laquelle la lumière est piégée et ne s’échappe pas vers les autres parties de la structure, la lumière est donc efficacement focalisée en cet endroit (Figure 5).
La structure-solution est-elle réellement optimale ?
En général, pour savoir si le procédé d’évolution est un succès, les chercheurs se fient à ce qu’on appelle la courbe de convergence produite par l’optimisation. Il s’agit de vérifier que, de génération en génération, l’algorithme d’optimisation parvient bien à générer des structures photoniques de plus en plus efficaces. Une courbe de convergence est tracée lorsqu’on représente sur un graphe la valeur de la fonction de mérite donnée par la meilleure des structures de la population en fonction du temps (du nombre de générations plus précisément). Après un nombre suffisant de générations, l’algorithme doit converger : il ne parvient plus à trouver une nouvelle structure qui améliore la valeur de la fonction de mérite. Si à la fin de l’optimisation, la convergence de l’algorithme n’est pas atteinte, les chercheurs en déduisent donc que l’optimisation a échoué.
Même si l’optimisation permet d’obtenir une bonne courbe de convergence, et qu’une structure solution est proposée, cela ne veut pas dire que l’algorithme a réussi à déterminer la structure optimale par rapport à l’objectif fixé. Cela veut seulement dire que l’algorithme est arrivé au bout de ses capacités d’amélioration de structures. L’une des pratiques permettant de contourner ce problème consiste à lancer plusieurs fois l’algorithme d’optimisation en partant à chaque fois de populations initiales différentes et de s’assurer que le procédé d’évolution aboutit à la même structure-solution indépendamment des structures initiales. Cette procédure permet d’attribuer plus de confiance en l’efficacité d’une structure, mais ne permet pas d’être sûr que la structure est optimale, puisqu’il faudrait pouvoir démontrer qu’il n’en existe pas de meilleures.
Gondarenko et son équipe ont effectué plusieurs optimisations et affirment qu’à chaque fois, la structure finale est similaire à la structure-solution décrite ci-dessus, bien que la valeur de la fonction de mérite ne soit pas à chaque fois strictement la même.
Le miroir de Bragg chez le scarabée
En partant de structures aléatoires — donc complètement irrégulières — Gondarenko et ses collègues aboutissent à une structure périodique (Figure 5). Or, les structures périodiques sont bien connues des physiciens car, en plus d’être facilement fabricables et compréhensibles (chaque motif périodique joue un rôle bien défini dans la réponse optique globale de la structure), elles sont présentes dans la nature ! On les retrouve chez certains scarabées [5], ou certains papillons [6]. Les travaux de Gondarenko laissent donc penser que concevoir des structures photoniques qui sont périodiques est une excellente façon de garantir l’efficacité optique de ces structures. Depuis, il a été découvert que parmi un grand nombre de méthodes d’optimisation, celle utilisée par Gondarenko et ses collègues reste l’une des plus efficaces pour découvrir des structures photoniques dont nous pouvons facilement comprendre le rôle physique [7] et que nous pouvons donc adapter à des besoins technologiques spécifiques.
[1] Macleod H. A., « Thin-film optical filters ». CRC press, 2017. ISBN : 978-1351982245. [Livre de science]
[2] Storn R. & Price K., Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. Journal of global optimization, 1997. DOI : 10.1023/A:1008202821328. [Publication scientifique]
[3] Dorigo M. & Di Caro G., Ant colony optimization: a new meta-heuristic. Proceedings of the 1999 congress on evolutionary computation-CEC99,1999. DOI : 10.1109/CEC.1999.782657. [Publication scientifique]
[4] « Particle swarm optimization », édité par A. Lazinica, 2009. ISBN : 9789537619480. [Livre de science]
[5] Stavenga D. G., et al., Polarized iridescence of the multilayered elytra of the Japanese jewel beetle Chrysochroa fulgidissima. Philosophical Transactions of the Royal Society B: Biological Sciences, 2011. DOI : 10.1098/rstb.2010.0197. [Publication scientifique]
[6] Kinoshita S., et al., Photophysics of structural color in the Morpho butterflies. Forma-Tokyo, 2002. [Publication scientifique]
[7] Barry M. A., et al.,Evolutionary algorithms converge towards evolved biological photonic structures. Scientific reports, 2020. DOI : 10.1038/s41598-020-68719-3. [Publication scientifique]

Merci pour cet article fort intéressant, connaissez-vous les champs d’application de cette structure?
Merci pour votre intérêt pour cet article !
De façon générale, les structures à fort confinement de la lumière peuvent être utilisées dans les circuits de communication optique, en tant que modulateurs ou d’interrupteurs. L’idée c’est de venir moduler des faisceaux lumineux, et en fonction de l’intensité du faisceau la communication ne sera pas la même. Plus une structure photonique peut focaliser la lumière, plus elle sera sensible au changement d’intensité d’un faisceau, et ainsi le circuit de communication sera globalement plus précis.
De plus, cette structure étant une cavité laser, elle peut-être utilisée dans tous les appareils nécessitant un faisceau de lumière d’une seule couleur qui se dirige dans une direction précise (pointeur laser, imprimante laser, etc).