Chargement de l'article...
Écriture : Alexandre Fauquette
Relecture scientifique : Thomas Merly-Alpa
Relecture de forme : Alexandre This et Pauline Colinet
Temps de lecture : environ 13 minutes.
Thématiques : Statistique & Probabilités (Mathématiques) ; Intelligence artificielle (Informatique et Sciences cognitives)
Publication originale : Auer P. et al., Finite-time Analysis of the Multiarmed Bandit Problem. Machine Learning, 2020 DOI : 10.1023/A:1013689704352

Prendre une décision est un problème complexe, mais il y a pire encore : prendre une décision sans en connaître à l’avance les conséquences. Pourtant notre monde est rempli d’incertitudes, et une intelligence artificielle digne de ce nom devra en être capable. L’article dont on parle ici présente l’un des principaux résultats théoriques sur la prise de décision dans un environnement incertain.
Comment prendre une bonne décision ?
Notre histoire commence par un défi. Votre amie vous tend deux pièces pour jouer à pile ou face, une bleue et une rouge. Les règles sont les suivantes. Vous avez le droit à 1000 lancers. Pour chaque lancer vous pouvez choisir entre la pièce rouge et la pièce bleue. Si vous faites pile, vous gagnez un point ; si c’est face, vous ne gagnez rien. Votre défi : gagner le plus de points possible avec ces 1000 lancers.
Évidemment ces pièces sont truquées ! L’une donne plus souvent pile que l’autre, mais vous ne savez pas laquelle.
Pour réussir ce défi, il va vous falloir trouver la pièce qui fait le plus souvent pile. On va donc tester la pièce rouge et la pièce bleue pour compter le nombre moyen de fois où ces pièces font pile. Mais combien de lancers doit-on utiliser pour trouver la meilleure pièce ? Si l’on teste trop, on va gaspiller des lancers. Mais si l’on ne teste pas assez, on risque de lancer la mauvaise pièce et de faire un score ridiculement bas ! Explorer les différentes pièces ou exploiter celle que vous pensez être la meilleure, voilà un dilemme compliqué !
Ce défi vous semble inutile ? À la place de nos pièces, imaginez des playlists de rap et de pop. Et remplacez l’événement « la pièce fait pile » par « l’utilisateur écoute la musique plus de 30 secondes » : vous obtenez la base du système de recommandation de Spotify. De nombreux systèmes de recommandations correspondent à ce problème. On doit choisir entre plusieurs options pour maximiser une récompense. Cela peut être : proposer des playlists, des publicités, ou encore envoyer un mail de rappel. La récompense sera alors le temps d’écoute, un achat ou une réponse. Les comportements humains ne sont pas entièrement prévisibles. C’est cet aspect imprévisible que l’on veut modéliser par l’aléatoire du jeu pile ou face.
Trouver la bonne pièce
Revenons à notre jeu. On cherche à obtenir la plus grosse récompense. Une fois que l’on a choisi si l’on souhaite jouer avec la pièce rouge ou bleue, on a deux possibilités : soit on obtient « pile » et on gagne un point, soit on obtient « face » et on n’obtient aucun point supplémentaire. 1 point et 0 point sont les gains de chacune des pièces. Imaginons que vous lanciez une pièce équilibrée deux fois. La première fois vous obtenez pile, vous avez un point. La seconde fois vous obtenez face, vous n’avez pas de point. En moyenne, vous avez donc 1 point sur 2 lancers, soit un gain moyen de 1/2 = 0,5. De même, si vous faite trois fois pile et deux fois face, vous obtenez 3 points sur 5 lancers, soit un gain moyen de 3/5 = 0,6.
À partir de là, on peut calculer le gain que l’on attend en moyenne après un très grand nombre de lancers, que l’on appelle l’espérance du gain d’une pièce.
Commençons par poser les notations mathématiques :
![Rendered by QuickLaTeX.com E[\mathrm{Gain}]](https://papiermachesciences.org/wp-content/ql-cache/quicklatex.com-7ee12f596a9015f7a0a638cb1921402a_l3.png) est l’espérance du gain de la pièce, c’est ce que l’on cherche à connaître.
est l’espérance du gain de la pièce, c’est ce que l’on cherche à connaître.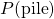 représente la probabilité que le lancer de la pièce donne un pile.
représente la probabilité que le lancer de la pièce donne un pile.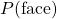 représente la probabilité que le lancer de la pièce donne un face.
représente la probabilité que le lancer de la pièce donne un face.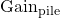 est la valeur gagnée lorsque le lancer donne pile. Il vaut 1 point.
est la valeur gagnée lorsque le lancer donne pile. Il vaut 1 point.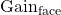 est la valeur gagnée lorsque le lancer donne face. Il vaut 0 point.
est la valeur gagnée lorsque le lancer donne face. Il vaut 0 point.
La formule s’écrit alors :
![]()
![]()
![]()
![]()
C’est-à-dire que l’espérance du gain de chaque pièce est égal à la probabilité de faire pile avec cette pièce.
Ben voilà, on a résolu le problème ! Il suffit de regarder la moyenne de chaque pièce et d’utiliser celle qui a la plus grande moyenne.
Séparer théorie et réalité
Que de précipitation ! L’espérance et la moyenne, ça se ressemble, mais ce n’est pas la même chose. L’espérance et les probabilités sont des valeurs théoriques que l’on ne peut voir que sur le long terme, avec un très grand nombre de lancers. Si vous avez déjà joué à pile ou face, vous savez que jouer deux fois ne garantit pas d’avoir une fois pile et une fois face. Pour renforcer la distinction entre la moyenne théorique qu’est l’espérance, et la moyenne que l’on peut mesurer par l’expérience, on parle de moyenne empirique pour désigner cette dernière.
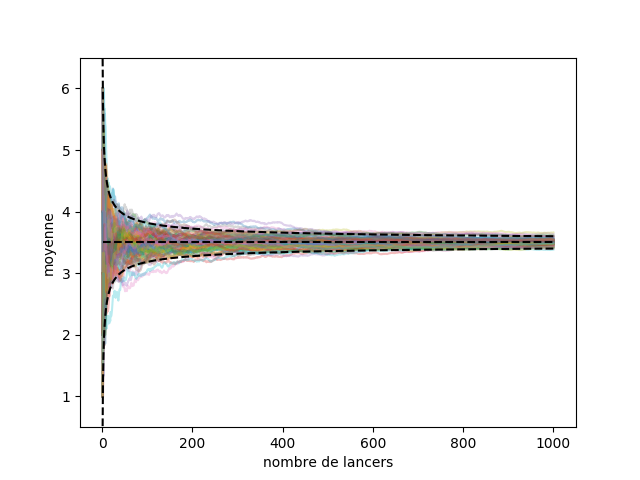
Sur la Figure 1, on a tracé la moyenne empirique d’une pièce équilibrée sur 1000 lancers. On voit clairement que la moyenne empirique (représentée par le trait bleu plein) n’est pas égale à l’espérance (représentée par les pointillés noirs). Même après 1000 lancers, il reste un écart.
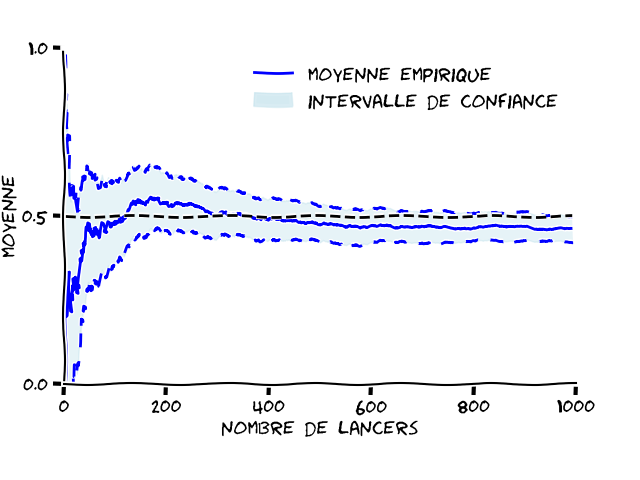
La moyenne empirique ne nous permet pas de trouver la valeur de l’espérance. Au lieu de chercher à donner une valeur exacte à l’espérance, on va plutôt donner un intervalle où l’espérance devrait se trouver. Pour être plus précis, sur la Figure 1, la probabilité que l’espérance soit dans l’intervalle en bleu clair est supérieure à 90 %. Cette probabilité de contenir la vraie valeur s’appelle le niveau de confiance. On parle alors d’un intervalle de confiance.
Vous pouvez constater que plus on fait de lancers, plus l’intervalle de confiance se rétrécit, et se rapproche de la moyenne empirique. Cela signifie que plus vous faites de lancers, plus vous avez confiance dans votre moyenne empirique. La bande de valeurs nécessaire pour avoir une confiance à 90 % dans la valeur de l’espérance peut donc être encore plus petite si vous faites plus de lancers.
On a donc maintenant un outil (l’intervalle de confiance) qui nous permet de savoir à quel point on est sûr de notre estimation. Ce qui peut être très utile comme information avant de tout miser sur la pièce rouge ou bleue. Il ne reste plus qu’à trouver comment utiliser cette information.
Des stratégies qui ne fonctionnent pas
Commençons par une stratégie simple, voire trop simple : décider à l’avance du nombre d’essais avant de choisir quelle pièce jouer. Vous avez pu le remarquer, plus on utilise de lancers pour calculer la moyenne empirique, plus l’intervalle de confiance est petit. Il faudrait donc utiliser assez de lancers de la pièce rouge et de la pièce bleue pour décider quelle est la meilleure pièce avec une grande confiance.
Utiliser l’intervalle de confiance est une superbe idée, mais ce niveau de confiance va dépendre des pièces. Prenons deux exemples extrêmes. Si l’espérance (théorique, donc) du gain de la pièce rouge est de 0,7 et celle de la pièce bleue 0,3, vous devriez assez vite déterminer que la pièce rouge est plus intéressante. Par contre, si l’espérance de la pièce rouge est de 0,6 et celle de la pièce bleue 0,5, il va falloir beaucoup plus de lancers pour vous apercevoir que la pièce rouge est meilleure que la pièce bleue.
C’est ce dilemme qui est représenté Figure 2 : la situation 1 présente le cas où les espérances des pièces rouge et bleue sont bien distinctes (0,7 et 0,3, respectivement). On peut alors se contenter de larges intervalles de confiance pour distinguer le gain de chaque pièce, et on a donc besoin de peu d’essais. La situation 2 présente des espérances plus proches (pièce rouge : 0,6 ; pièce bleue : 0,5). Avec le même intervalle de confiance que dans la situation 1, il devient impossible de départager les deux pièces pour comprendre laquelle est la meilleure. Pour réussir à les distinguer, il faudra donc réduire davantage l’intervalle de confiance pour éviter qu’ils ne se superposent, c’est ce qui est illustré à la situation 3. Réduire un intervalle de confiance, comme on l’a vu sur la Figure 1, nécessite de faire davantage de lancers.
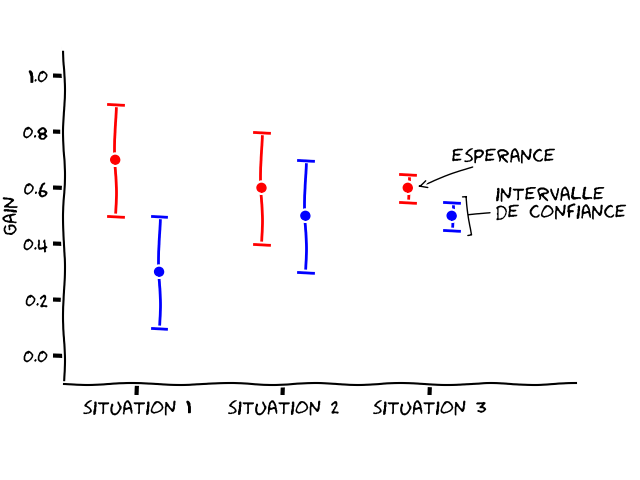
Conclusion sur cette stratégie : fixer à l’avance le nombre d’essais n’est pas possible, car le nombre de lancers nécessaires pour distinguer les deux pièces dépend de la valeur de leur espérance. Or, c’est justement cette valeur-là que l’on cherche. C’est un serpent qui se mord la queue ! Il nous faut donc une stratégie un peu plus complexe !
La stratégie UCB
Voici la solution proposée par les chercheurs dans la publication qui nous intéresse aujourd’hui. Les auteurs l’ont baptisée UCB pour Upper Confidence Bound (ou borne supérieure de l’intervalle de confiance, en français) qui est une stratégie dite optimiste. Regardons comment elle fonctionne.
La Figure 3 représente deux autres situations. Vous pouvez voir que la moyenne empirique de la pièce rouge est dans les deux cas plus élevée que celle de la bleue (0,8 pour la rouge et 0,6 pour la bleue). De plus, la pièce bleue a un intervalle de confiance plus large dans les deux situations. Ce qui signifie que l’on a moins testé la pièce bleue que la pièce rouge. Dans ces situations, vaut-il mieux jouer la pièce rouge ou la pièce bleue ? La rouge semble plus intéressante, car sa moyenne empirique est plus haute que celle de bleue. Mais la pièce bleue a une forte incertitude. Il se pourrait alors que l’espérance de la pièce bleue soit en réalité plus grande que celle de la rouge. Il faudrait alors lancer la pièce bleue pour réduire son incertitude.
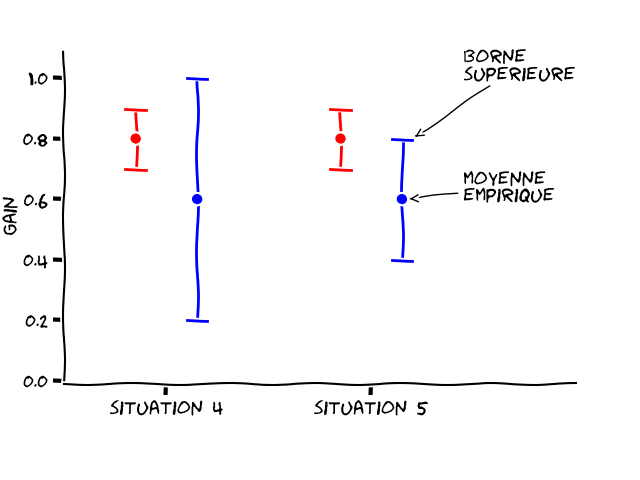
La première possibilité revient à faire confiance aux moyennes empiriques, en exploitant la pièce qui semble être la plus rentable, soit la rouge. La deuxième possibilité est d’explorer la pièce bleue, même si elle n’a pas la meilleur moyenne. Cette exploration nous permettrait d’éviter de choisir la mauvaise pièce.
Pour choisir entre exploration et exploitation, la stratégie UCB vous conseille de ne pas regarder la moyenne empirique pour prendre votre décision, ni la taille de l’intervalle de confiance, mais plutôt de vous intéresser à la borne supérieure de l’intervalle de confiance. En effet, un optimiste ne va pas se dire « l’espérance est comprise dans cet intervalle ». Un optimiste va se dire « avec un peu de chance, l’espérance est tout en haut de cet intervalle ».
Prenons la situation 4 de la Figure 3. L’intervalle de confiance bleu va plus haut que l’intervalle de confiance rouge. Notre optimiste va donc choisir la pièce bleue, car c’est cette pièce qui peut potentiellement donner le plus gros gain. En lançant cette pièce plusieurs fois, il réduit son intervalle de confiance. Il se retrouve alors dans la situation 5. L’intervalle de confiance de la pièce bleue est réduit, et la moyenne était probablement bien évaluée, car elle n’a pas bougé avec ces lancers. Maintenant que l’on a confirmé que jouer la pièce bleue n’était pas si intéressant que ça, et que la borne supérieure la plus haute est désormais celle de la pièce rouge, c’est elle que l’on va jouer, jusqu’à ce que la borne supérieure de son intervalle de confiance passe à nouveau sous celle de la pièce bleue. À ce moment-là, on confirmera en jouant la pièce bleue que la moyenne de bleue n’est pas tout en haut de l’intervalle de confiance (ce qui en ferait le choix privilégié), et ainsi de suite.
Et voilà, ce n’est pas plus compliqué que cela : calculer l’intervalle de confiance, jouer la pièce dont l’intervalle de confiance a la borne supérieure la plus haute, et recommencer. Cette stratégie, UCB, est intéressante car simple à calculer. Mais surtout, on peut démontrer que le nombre de fois où vous allez lancer la mauvaise pièce est très faible.
Garanties
Cette stratégie apporte une garantie assez forte : sur N (un nombre entier quelconque) lancers, le nombre de fois où vous allez choisir la mauvais pièce est très faible. Il est de l’ordre de log(N), c’est à dire qu’il suit une croissance logarithmique. Vous ne savez pas ce qu’est une croissance logarithmique ? En voici un exemple :
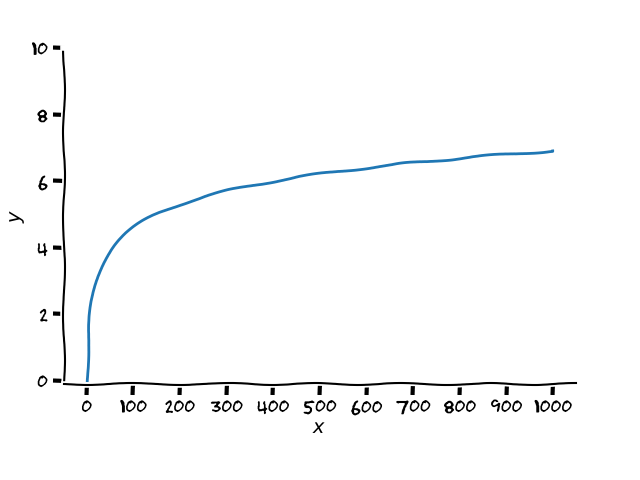
C’est l’une des fonctions les plus lentes. Et c’est très bien dans notre cas, car cela veut dire que quand on continue à jouer (que l’on augmente N le nombre de lancers), le nombre d’erreurs n’augmente presque pas. D’ailleurs, il a été montré que le nombre d’erreurs théoriques ne pourrait dans tous les cas pas être plus faible que log(N). Cette stratégie est donc très performante [1] !
Intuition de la preuve
Pour vous convaincre que cette stratégie fonctionne vraiment bien, je ne peux pas vous faire la démonstration complète qui demande des notions plus approfondies de mathématiques, mais je peux vous donner une idée de comment démontrer ce genre de résultat.
Pour simplifier le problème, imaginons que l’on a le choix entre une pièce dorée et une pièce argentée, la pièce dorée ayant une espérance de gain plus grande que la pièce argentée. La question est donc : sur N lancers, quel est le nombre maximal de fois où la pièce argentée sera choisie ?
Comme on utilise UCB, cela revient à compter le nombre de fois où le maximum de l’intervalle de confiance associé à la pièce argentée est supérieur à celui de la pièce dorée. Si l’on pose l’équation, on peut montrer qu’il faut au moins qu’une des trois conditions suivantes soit vérifiée pour que UCB préfère la pièce argentée à la dorée :
- la moyenne empirique de la pièce dorée sous-estime largement la vraie moyenne ;
- la moyenne empirique de la pièce argentée surestime largement la vraie moyenne ;
- l’intervalle de confiance associé à la pièce argentée est beaucoup trop grand.
Les deux premiers cas correspondent aux moments où, par chance ou malchance, les gains obtenus sont très différents que ce que l’on aurait pu espérer (par exemple, on avait 1 chance sur deux de gagner, mais en fait on a gagné 5 fois d’affilée). Dans ces cas, la moyenne empirique sort de l’intervalle de confiance. Or, l’intervalle de confiance est conçu, par définition, pour que la probabilité d’en sortir diminue très vite. Tellement vite que ces deux premiers cas sont négligeables : ils n’arrivent que très rarement, trop rarement pour que notre stratégie les prenne en compte.
Il reste donc le cas où l’on choisit la mauvaise pièce car l’intervalle de confiance est trop grand. Vous l’aurez deviné, c’est ce dernier cas qui est responsable de la croissance logarithmique log(N) du nombre d’erreurs. Si vous vous rappelez de la Figure 3, on a dû jouer la pièce bleue pour diminuer son intervalle de confiance et s’assurer que la pièce rouge était bien la meilleure. Sur N lancers, il faudra donc utiliser log(N) lancers de la mauvaise pièce pour diminuer suffisamment son intervalle de confiance. Ce qui est aussi peu que l’on puisse espérer.
Conclusion
Vous avez maintenant une stratégie dont vous pouvez prouver que le nombre d’erreurs que vous ferez sera proche de la limite théorique. Pour jouer à pile ou face, ce n’est peut être pas très utile, mais le publicitaire ou les systèmes de recommandations ont un grand intérêt à avoir des stratégies qui font le moins d’erreurs possibles.
Évidemment, les chercheurs ne se sont pas arrêtés à ce problème de pile ou face à deux pièces. Habituellement l’image utilisée est celle des machines à sous. Le problème est le même : trouver la machine qui a la meilleure espérance. Mais on n’a plus que deux machines, et surtout les événements possibles sont plus variés que pile/face.
À partir de ce problème, des chercheuses et chercheurs se sont demandés comment faire si l’espérance des machines dépend de leur position dans le casino. Ou que faire si l’espérance des gains évolue au cours du temps. Il y a de nombreuses variantes que l’on réunit sous le nom de problème des bandits manchots, car les machines à sous dans les casinos s’appellent des bandits manchots. Elles vous volent votre argent et n’ont qu’un seul bras, le levier à tirer pour la faire fonctionner. Ces variantes sont nombreuses, mais c’est toujours la même idée : contrôler l’incertitude pour prendre une bonne décision.
Petit rappel avant de se quitter, les jeux d’argent sont d’excellents moyens de parler de probabilités. Mais dans la vraie vie, toutes les machines sont perdantes en moyenne. Jouer comporte des risques, ne les négligeons pas. Pour plus d’informations, rendez-vous sur https://www.joueurs-info-service.fr/.
[1] La publication scientifique historique sur la borne minimale : Lai T.L. & Robbins H., Asymptotically efficient adaptive allocation rules. Advances in Applied Mathematics, 1985. DOI : 10.1016/0196-8858(85)90002-8
Écriture : Alexandre Fauquette
Relecture scientifique : Thomas Merly-Alpa
Relecture de forme : Alexandre This
Temps de lecture : environ 15 minutes.
Thématiques : Statistique & Probabilités (Mathématiques) ; Intelligence artificielle (Informatique et Sciences cognitives)
Publication originale : Auer P. et al., Finite-time Analysis of the Multiarmed Bandit Problem. Machine Learning, 2020 DOI : 10.1023/A:1013689704352

Prendre une décision est un problème complexe, mais il y a pire encore : prendre une décision sans en connaître à l’avance les conséquences. Pourtant notre monde est rempli d’incertitudes, et une intelligence artificielle digne de ce nom devra en être capable. L’article dont on parle ici présente l’un des principaux résultats théoriques sur la prise de décision dans un environnement incertain.
Comment prendre une bonne décision ?
Notre histoire commence par un défi. Vous vous trouvez avec une mathématicienne dans un casino un peu particulier, il contient 3 machines différentes. Votre amie vous tend 1000 jetons d’un air malicieux et vous met au défi de gagner le plus d’argent possible avec ces 1000 jetons. Les machines de ce casino sont différentes : pour un jeton joué, le gain moyen n’est pas le même partout. Évidemment, le gain moyen de chaque machine est top secret ! Et votre amie ne vous a évidemment pas dit quelle machine est la plus généreuse en moyenne.
Pour répondre à ce défi, une stratégie consiste à chercher la meilleure machine. Il faut donc commencer par toutes les tester. Mais combien de jetons faut-il consacrer à ces tests ? Si vous passez trop de temps à tester les machines, vous gaspillez vos jetons. Mais si vous ne testez pas assez, vous risquez de tout miser sur la mauvaise machine. Explorer les différentes machines ou exploiter celle que vous pensez être la meilleure, voilà un dilemme compliqué !
Cette histoire de casino vous semble tirée par les cheveux ? Remplacez les machines à sous par des playlists musicales, et le jackpot par le fait qu’un utilisateur écoute plus de 30 secondes la musique, et vous obtenez la base du moteur de recommandation de Spotify. De nombreux systèmes de recommandations correspondent à ce problème : on doit choisir entre plusieurs options (les machines) pour maximiser une récompense (une interaction avec l’utilisateur). Les comportements humains ne sont pas entièrement prévisibles ; cela correspond au côté aléatoire des machines à sous.
Sans plus attendre : la solution
Vous voulez la solution du problème ? Avant cela, il faut se demander à partir de quand on considère qu’une solution est bonne. Est-ce que l’on sera content si l’on ne s’est trompé de machine que 10 fois, 100 fois ou 200 fois ? En 1985, T.L Lai et Herbert Robbins ont démontré que lorsque le nombre de jetons tend vers l’infini, on va se tromper de machine au moins un nombre logarithmique de fois [1]. Autrement dit, pour un nombre de jetons T grand, on est obligé d’en utiliser un certain nombre pour tester les différentes machines. Ce nombre d’erreurs grandit comme log(T) que l’on note habituellement ![]() (log(T)). Pour être précis, si vous trouvez une stratégie qui fait moins de log(T) essais, il existe au moins un casino dans lequel elle se trompera royalement. En plus de ce résultat, ils donnent une méthode qui, lorsque T tend vers l’infini, se trompe au plus
(log(T)). Pour être précis, si vous trouvez une stratégie qui fait moins de log(T) essais, il existe au moins un casino dans lequel elle se trompera royalement. En plus de ce résultat, ils donnent une méthode qui, lorsque T tend vers l’infini, se trompe au plus ![]() (log(T)) fois.
(log(T)) fois.
Génial ! ces deux chercheurs ont réussi à prouver que pour T tendant vers l’infini, on ne peut pas faire moins que ![]() (log(T)) erreurs. Et ils proposent une méthode qui garanti un nombre d’erreur lui aussi en
(log(T)) erreurs. Et ils proposent une méthode qui garanti un nombre d’erreur lui aussi en ![]() (log(T)). On sait donc qu’une bonne solution doit faire asymptotiquement
(log(T)). On sait donc qu’une bonne solution doit faire asymptotiquement ![]() (log(T)) erreurs. Cependant, votre amie vous a donné 1000 jetons. C’est beaucoup, mais pas une infinité. De plus, je ne vous l’ai pas dit, mais la solution qu’ils proposent est un peu complexe à calculer. Heureusement pour vous, en 2002, P. Auer, N. Cesa-Bianchi et P. Fisher ont proposé une méthode avec un résultat garanti pour un nombre de jetons T fini, qui donne aussi un nombre d’erreurs en
(log(T)) erreurs. Cependant, votre amie vous a donné 1000 jetons. C’est beaucoup, mais pas une infinité. De plus, je ne vous l’ai pas dit, mais la solution qu’ils proposent est un peu complexe à calculer. Heureusement pour vous, en 2002, P. Auer, N. Cesa-Bianchi et P. Fisher ont proposé une méthode avec un résultat garanti pour un nombre de jetons T fini, qui donne aussi un nombre d’erreurs en ![]() (log(T)). En plus leur méthode est nettement plus simple à mettre en place !
(log(T)). En plus leur méthode est nettement plus simple à mettre en place !
Pour chaque machine a, vous devez connaître na qui est le nombre de jetons déjà joués avec cette machine, et ![]() la moyenne empirique des récompenses de cette même machine. À chaque fois que vous jouez la machine a, il faudra augmenter na de 1 et mettre à jour
la moyenne empirique des récompenses de cette même machine. À chaque fois que vous jouez la machine a, il faudra augmenter na de 1 et mettre à jour ![]() pour prendre en compte la récompense obtenue. Dernière information à connaître : t le nombre de jetons déjà utilisés sur l’ensemble des machines. Vous connaissez les ingrédients (
pour prendre en compte la récompense obtenue. Dernière information à connaître : t le nombre de jetons déjà utilisés sur l’ensemble des machines. Vous connaissez les ingrédients (![]() , na et t). Il ne manque plus que la recette.
, na et t). Il ne manque plus que la recette.
Pour maximiser votre récompense, vous devez :
- Calculer pour chaque machine a son indice donné par la formule suivante :
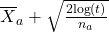
- Jouer la machine qui a le plus grand indice.
- Utiliser la récompense obtenue pour mettre à jour vos valeurs (
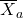 et na) puis recommencer.
et na) puis recommencer.
Une solution optimiste
Le terme de gauche ![]() ne devrait pas vous surprendre. On cherche la machine qui donne le meilleur résultat en moyenne. Il est donc logique de calculer la moyenne de ses résultats. Le problème c’est qu’avec la moyenne seule nous n’avons pas assez d’informations. Tentons de comprendre pourquoi.
ne devrait pas vous surprendre. On cherche la machine qui donne le meilleur résultat en moyenne. Il est donc logique de calculer la moyenne de ses résultats. Le problème c’est qu’avec la moyenne seule nous n’avons pas assez d’informations. Tentons de comprendre pourquoi.
Imaginez que je lance un dé pour vérifier qu’il n’est pas truqué. La moyenne des points obtenus devrait être de 3,5 (l’espérance d’un dé classique non truqué). Pourtant au début je ne pas vais pas forcément trouver cette valeur. La Figure 1 montre l’évolution de la moyenne empirique calculée sur 1000 lancers de dé. On voit qu’il faut attendre un certain nombre de lancers avant de s’approcher des 3,5 attendus. On a donc d’un côté la moyenne théorique du dé que l’on appelle espérance ![]() 3,5 et de l’autre la moyenne mesurée
3,5 et de l’autre la moyenne mesurée ![]() qui est aléatoire mais se rapproche de
qui est aléatoire mais se rapproche de ![]() 3,5 quand t grandit.
3,5 quand t grandit.
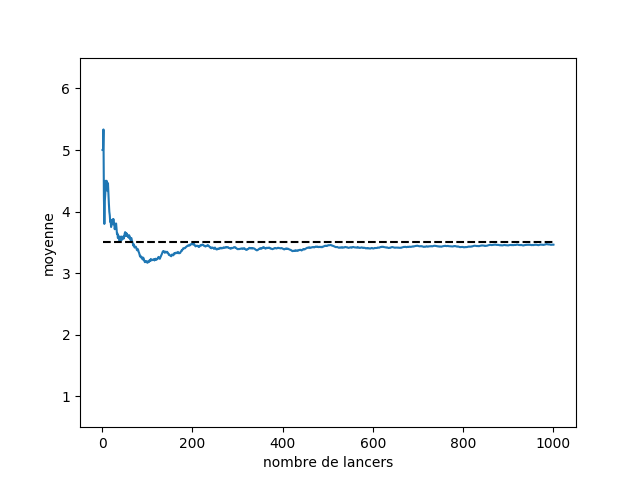
On a répété cette expérience 100 fois sur la Figure 2. On voit que toutes les moyennes se rapprochent de l’espérance quand le nombre de lancers augmente, un peu comme si elles entraient dans un goulot d’étranglement. On est capable de mesurer ce rapprochement, grâce aux inégalités de concentration. L’inégalité que l’on va utiliser ici est celle de Chernoff-Hoeffding qui dit (sous certaines conditions) que :
![]() et
et ![]()
On peut regrouper ces deux inégalités pour obtenir :
![]()
On parle alors d’un intervalle de confiance. Mais une valeur pour approximer l’espérance ![]() , ce n’est pas assez informatif. En complément, on propose l’intervalle
, ce n’est pas assez informatif. En complément, on propose l’intervalle ![]() qui va nous donner le niveau de confiance la valeur
qui va nous donner le niveau de confiance la valeur ![]() . Cet intervalle est construit pour être suffisamment étroit, tout en garantissant que la probabilité qu’il contienne
. Cet intervalle est construit pour être suffisamment étroit, tout en garantissant que la probabilité qu’il contienne ![]() soit plus grande que
soit plus grande que ![]() . Évidemment, plus l’intervalle est grand, plus il est facile d’avoir un niveau de confiance élevé. Le cas extrême étant de dire que
. Évidemment, plus l’intervalle est grand, plus il est facile d’avoir un niveau de confiance élevé. Le cas extrême étant de dire que ![]() est compris entre
est compris entre ![]() et
et ![]() avec une probabilité de 1. Le niveau de confiance est maximal, mais l’intervalle est infiniment trop large pour apporter une information utile.
avec une probabilité de 1. Le niveau de confiance est maximal, mais l’intervalle est infiniment trop large pour apporter une information utile.
Vous avez sans doute remarqué le lien avec notre formule de départ : ![]() . En prenant
. En prenant ![]() , on retrouve effectivement la formule de l’indice. De plus, on obtient que la probabilité que
, on retrouve effectivement la formule de l’indice. De plus, on obtient que la probabilité que ![]() soit supérieur à
soit supérieur à ![]() est inférieure à
est inférieure à ![]() . Le choix d’utiliser
. Le choix d’utiliser ![]() peut vous sembler arbitraire. Mais quand on rédige la preuve, on réalise que les événements ayant une probabilité de l’ordre de
peut vous sembler arbitraire. Mais quand on rédige la preuve, on réalise que les événements ayant une probabilité de l’ordre de ![]() peuvent être négligé. C’est donc pour pouvoir négliger ces situations que l’on prend comme indice
peuvent être négligé. C’est donc pour pouvoir négliger ces situations que l’on prend comme indice ![]() .
.
Pour information, cet algorithme s’appelle UCB pour Upper Confidence Bound, qui peut se traduire par « borne supérieure de l’intervalle de confiance ». Il porte bien son nom, car on compare les machines en utilisant la borne supérieure de leur intervalle de confiance. Si vous voulez une interprétation plus humaine, sachez que l’on parle de stratégie optimiste. Avec cette stratégie, vous ne jouez pas la machine avec la meilleure moyenne. Vous jouez celle qui pourrait avoir la meilleure moyenne pour un niveau de confiance fixé. En effet, dans cette situation, un optimiste va se dire « avec un peu de chance, l’espérance est tout en haut de cet intervalle de confiance ».
Pour vous convaincre de l’intérêt d’être optimiste, prenez l’évolution présentée à la Figure 3. On a une machine bleue et une machine rouge dont l’espérance des gains est respectivement 0,5 (bleue) et 0,6 (rouge). Sur la figure, vous pouvez voir l’évolution des moyennes empiriques de ces deux machines. Pendant les 50 premiers essais, on pourrait penser que la machine bleue est meilleure que la rouge, et il faut attendre environ 200 essais avant que l’on puisse clairement voir une distinction entre les machines bleue et rouge.
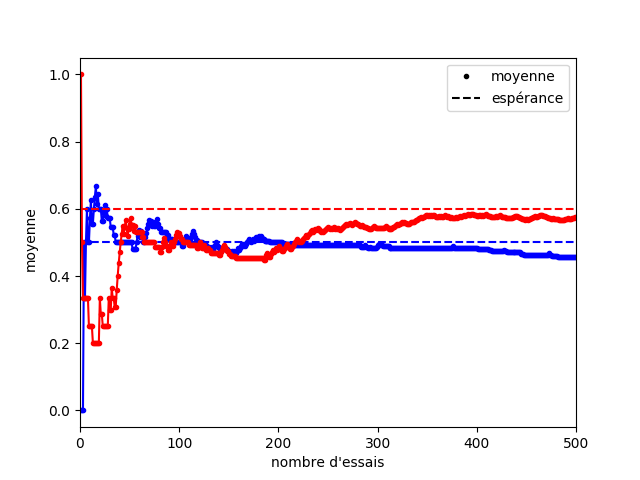
Dans cet exemple, si vous vous fiez uniquement à la moyenne au début, c’est la catastrophe ! La moyenne de la machine bleue est surestimée, et celle de la machine rouge rouge sous-estimée. Heureusement, l’indice qui correspond à la borne supérieure de l’intervalle de confiance permet de prendre en compte la part d’erreur contenue dans le hasard des premiers coups (Figure 4).
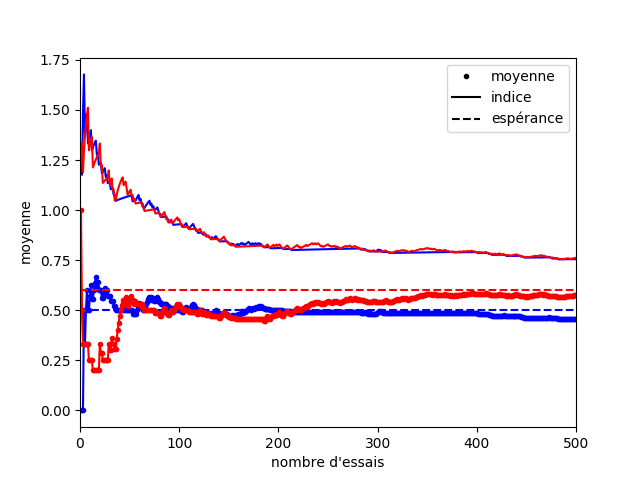
Si maintenant on regarde l’évolution de notre stratégie sur la Figure 5, on peut voir que malgré le manque de chance que nous avons eu au début, la machine rouge devient rapidement la plus utilisée. La machine bleue est quand même testée de temps en temps pour s’assurer que sa moyenne est bien estimée. Cette vérification se fait de moins en moins souvent, car on gagne en confiance sur notre estimation. On peut voir deux régimes sur ce graphique. Au début, les machines rouge et bleue sont testées toutes deux un nombre de fois similaires. Puis au bout d’un moment (200 essais) le nombre d’essais avec la machine bleue ralenti. On rentre dans un régime où le nombre d’erreurs suit une croissance logarithmique.
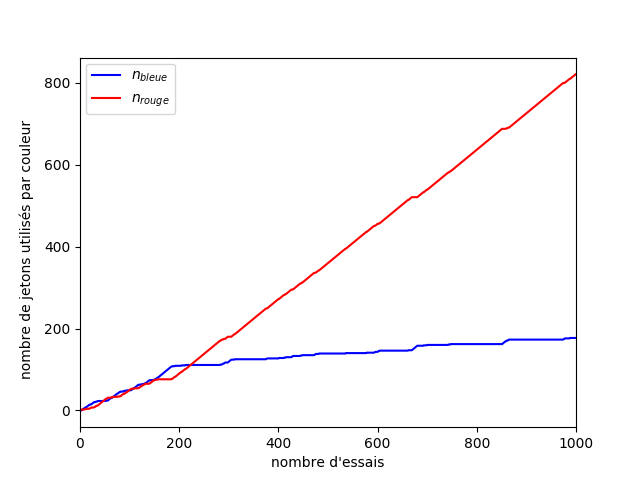
L’avantage des stratégies optimistes, c’est que soit vous jouez la bonne machine et c’est super ! Soit vous vous trompez et cela va réduire l’intervalle de confiance : vous choisirez alors mieux votre machine au tour suivant. Vous êtes gagnant dans les deux cas.
Et la preuve dans tout ça ?
Vous vous demandez sans doute comment on peut prouver qu’à tout moment le nombre d’erreurs de l’algorithme UCB est en ![]() (log(T)). L’idée générale, c’est de majorer le nombre de fois où l’on teste une machine a qui n’est pas optimale. Par convention, on note la meilleure machine avec une étoile.
(log(T)). L’idée générale, c’est de majorer le nombre de fois où l’on teste une machine a qui n’est pas optimale. Par convention, on note la meilleure machine avec une étoile.
Si vous avez joué la machine a à un instant t, c’est qu’à ce moment, l’indice de la machine a : ![]() était plus grand que l’indice de toutes les autres machines. Et donc il était plus grand que celui de la meilleure machine. Pour simplifier le problème, on ne va pas compter le nombre de fois où l’on a joué la machine a mais le nombre de fois où on aurait préféré jouer la machine a au lieu de étoile (la meilleure machine). Ce qui correspond à trouver le nombre de fois où :
était plus grand que l’indice de toutes les autres machines. Et donc il était plus grand que celui de la meilleure machine. Pour simplifier le problème, on ne va pas compter le nombre de fois où l’on a joué la machine a mais le nombre de fois où on aurait préféré jouer la machine a au lieu de étoile (la meilleure machine). Ce qui correspond à trouver le nombre de fois où :
![]()
La suite de la preuve consiste à décomposer cette inégalité en trois. Si notre inégalité est vraie, alors au moins l’une des inégalités suivantes est vraie :
C’est un résultat classique sur les inégalités : si A < B alors vous pouvez prendre n’importe quels nombres C et D et vous aurez A < C ou D < B ou C < D. Pour obtenir le triplet ci-dessus, il faut prendre C = ![]() et
et ![]()
Comme l’inégalité qui nous intéresse implique au moins l’une des trois inégalités précédentes, on peut majorer la probabilité de préférer la machine a à la meilleur machine comme ceci :
![]()
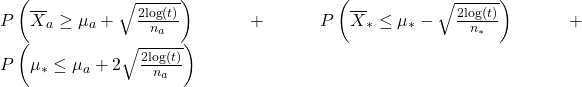
La probabilité que la première inégalité soit vraie est inférieure à ![]() grâce à l’inégalité de concentration de Chernoff-Hoeffding dont on a parlé précédemment. C’est exactement la même chose pour la deuxième inégalité. Il ne nous reste plus que la troisième. Cette inégalité est fausse lorsque
grâce à l’inégalité de concentration de Chernoff-Hoeffding dont on a parlé précédemment. C’est exactement la même chose pour la deuxième inégalité. Il ne nous reste plus que la troisième. Cette inégalité est fausse lorsque ![]() .
.
Comme par définition ![]() , on peut simplifier l’inéquation par
, on peut simplifier l’inéquation par ![]() . Donc pour
. Donc pour ![]() la troisième probabilité est nulle. On obtient alors :
la troisième probabilité est nulle. On obtient alors :
![]()
Cette implication nous dit que quand ![]() dépasse
dépasse ![]() , la probabilité de préférer la machine a est négligeable. On a donc bien un nombre d’erreurs en
, la probabilité de préférer la machine a est négligeable. On a donc bien un nombre d’erreurs en ![]() (log(T)). En fait, l’inégalité exacte est la suivante, mais les calculs qui permettent d’y arriver ne présentent pas d’intérêt. Si cela vous intéresse, vous pouvez aller lire la preuve dans la publication originale [2] .
(log(T)). En fait, l’inégalité exacte est la suivante, mais les calculs qui permettent d’y arriver ne présentent pas d’intérêt. Si cela vous intéresse, vous pouvez aller lire la preuve dans la publication originale [2] .
![]()
Conclusion : si vous suivez la stratégie UCB que l’on vient de présenter qui, pour rappel, vous demande de calculer à chaque fois l’indice ![]() pour toutes les machines et de jouer un jeton dans la machine ayant le plus grand indice, alors vous avez la garantie (en espérance) que le nombre de fois où vous jouerez une mauvaise machine a ne peut pas dépasser :
pour toutes les machines et de jouer un jeton dans la machine ayant le plus grand indice, alors vous avez la garantie (en espérance) que le nombre de fois où vous jouerez une mauvaise machine a ne peut pas dépasser :
![]()
Fini de jouer au petit bonheur la chance : vous avez maintenant une stratégie dont l’efficacité est prouvée !
Pour aller plus loin
Cette méthode est la première d’une longue série. Il y a eu des améliorations de l’algorithme, comme KL-UCB dont les garanties sont encore plus proches de la limite théorique que UCB [3]. En effet, on sait que asymptotiquement, le nombre d’erreurs est un ![]() (log(T)). Le résultat est plus précis que cela, car on connaît le coefficient devant le logarithme. Eh bien KL-UCB obtient une garantie avec exactement ce coefficient.
(log(T)). Le résultat est plus précis que cela, car on connaît le coefficient devant le logarithme. Eh bien KL-UCB obtient une garantie avec exactement ce coefficient.
Le fonctionnement de KL-UCB est très proche de UCB. Dans les deux cas, on regarde toutes les configurations de machines crédibles et on va jouer sur la machine qui pourrait avoir la meilleure récompense parmi toutes les possibilités crédibles.
La différence, c’est la définition de ce qui est crédible. Dans UCB, on considère comme crédibles toutes les configurations dont la moyenne est dans l’intervalle de confiance. Alors que dans KL-UCB, on utilise la divergence de Kullback-Leibler (notée KL) pour quantifier l’écart entre nos observations et une configuration de machines.
Les chercheur·e·s ont aussi créé plein de variantes du problème : que se passe-t-il si l’on sait que des machines proches donnent des récompenses similaires ? Comment agir si l’on sait que les machines sont truquées ? Comment faire face à une infinité de machines ? Que se passe-t-il si l’on est plusieurs à jouer dans le casino ?
Les variations de ce problème sont nombreuses, mais c’est toujours la même idée : contrôler l’incertitude pour prendre une bonne décision. Si vous voulez en savoir plus sur le sujet, Emilie Kaufmann, chercheuse à l’Inria, a présenté un excellent exposé Math Park que vous pouvez retrouver ici.
Petit rappel avant de se quitter, les jeux d’argent sont d’excellents moyens de parler de probabilités. Mais dans la vraie vie, toutes les machines sont perdantes en moyenne. Jouer comporte des risques, ne les négligeons pas. Pour plus d’informations, rendez-vous sur https://www.joueurs-info-service.fr/.
[1] La publication scientifique historique sur la borne minimale : Lai T.L. & Robbins H., Asymptotically efficient adaptive allocation rules. Advances in Applied Mathematics, 1985. DOI : 10.1016/0196-8858(85)90002-8
[2] La preuve complète d’UCB est accessible dans la publication originale. Il s’agit du théorème 1 et de la preuve associée.
[3] La publication scientifique d’origine sur KL-UCB : Garivier A. & Cappé O., The KL-UCB Algorithm for Bounded Stochastic Bandits and Beyond. Conference On Learning Theory, 2011.