Chargement de l'article...
Écriture : Jennifer Renoux
Relecture scientifique : Cédric Buron et Vincent Thomas
Relecture de forme : Aurélien Didier, Alexandre Fauquette et Christine Duthoit
Temps de lecture : environ 11 minutes.
Thématiques : Intelligence artificielle (Informatique et Sciences cognitives)
Publication originale : Spaan M., et al., Decision-theoretic planning under uncertainty with information rewards for active cooperative perception. Autonomous Agents and Multi-Agent Systems, 2014. DOI : 10.1007/s10458-014-9279-8

Les bons joueurs de Cluedo sont efficaces dans leur recherche d’information : ils planifient leurs actions afin d’obtenir le plus d’information possible en un minimum de temps. On appelle ce processus perception active, et c’est une capacité que les humains maîtrisent très bien. Pour les machines, en revanche, c’est plus compliqué. Dans un article de 2015, Matthijs Spaan, Tiago Veiga et Pedro U. Lima ont proposé un modèle dotant les machines de capacités de perception active, avec des applications dans le domaine de la robotique autonome pour la surveillance ou le sauvetage de personnes.
Perception active et planification sous incertitude. Kesako ?
En tant qu’humain, lorsque que l’on marche dans la rue, on absorbe de l’information sur ce qui se passe autour de nous : le feu piéton au vert, le tram qui arrive en station ou le fait que le bâtiment où l’on va se trouve droit devant nous. Ces informations sont intégrées par notre cerveau presque inconsciemment pendant qu’il est occupé à planifier la prochaine action pour nous amener à notre but final : notre rendez-vous chez le docteur. Quand on souhaite remplacer l’humain par un robot, un ordinateur ou n’importe quelle entité artificielle (appelée agent artificiel, souvent abrégé en agent), et lui permettre de planifier une séquence d’actions, on tombe dans un sous-domaine de l’Intelligence Artificielle, qui s’appelle la Planification Automatique. Dans le monde de la planification automatique, la plupart des problèmes considérés suivent ce schéma : l’agent calcule un plan lui permettant d’accomplir sa mission, et l’information qu’il obtient lors de l’exécution de ce plan est au service de la mission. La recherche d’information est alors un moyen pour atteindre un but et non le but en lui-même. Cependant, il existe certains cas d’applications où la recherche d’information n’est pas seulement un moyen pour l’agent d’atteindre un but mais constitue le but en lui-même. C’est par exemple le cas dans des applications de surveillance et de patrouille, mais aussi de recherche et de sauvetage, où la vie de personnes dépend de la capacité des sauveteurs et sauveteuses (humain·e·s ou artificiel·le·s) à collecter de l’information vite et bien.
Ce processus s’appelle la Recherche active d’information ou Perception Active. Le but ici est de collecter le plus d’information possible à propos de certains points d’intérêts. Pensez notamment à une partie de Cluedo, où il vous faut trouver le coupable, l’arme et le lieu du crime. Vous devez donc vous déplacer dans l’environnement et récolter de l’information afin d’éliminer, les uns après les autres, suspect·e·s, armes, et lieux potentiels.
Pour un humain, la perception active est simple. On la pratique depuis qu’on est gamin·e, quand on joue à cache-cache ou quand on cherche nos clefs. Notre cerveau y est entraîné. Mais comme souvent dans le domaine de l’Intelligence Artificielle, ce qui est facile pour un humain peut être très compliqué pour un agent artificiel. La perception active se fonde sur un modèle de connaissances de l’agent : il faut que l’on soit capable de modéliser ce que l’agent va considérer comme une certitude, mais également ce qu’il doit vérifier.
Dans cet article, les auteurs se placent dans le cadre de la planification séquentielle sous incertitude : on souhaite trouver la meilleure séquence d’actions possible afin d’atteindre un but donné, tout en sachant que l’on ne connaît pas tout de l’environnement. Dans le cas de votre rendez-vous chez le docteur, vous allez tenter de trouver la meilleure suite d’actions (quel tram prendre, tourner à droite à la seconde rue, etc.) pour arriver chez le docteur le plus rapidement possible. Pour ce faire, une solution possible est d’attribuer une valeur à certains états et certaines actions que l’on juge désirables. Par exemple, l’état « je suis chez mon docteur » aura une forte valeur positive car c’est l’état que l’on souhaite obtenir. En revanche, l’état « je suis immobile sur la ligne de tram » aura une très forte valeur négative car c’est particulièrement dangereux. On va donc récompenser notre agent lorsqu’il est dans état désirable ou effectue une action désirable, et le pénaliser s’il est dans un état ou effectue une action non désirable. Dans ce cas, ce qu’on appelle récompense ou pénalité correspond à cette valeur mathématique que l’on attribue aux différents états et actions et qu’on l’on donne à l’agent lorsqu’il se trouve dans cet état ou effectue cette action. Le but de l’agent (= la façon dont il est programmé) va être de maximiser sa récompense, immédiate et potentielle.
Le problème, c’est que dans la vraie vie, on n’a pas accès à toute l’information tout le temps. Par exemple, peut-être que le tram est au prochain croisement ou peut-être qu’il est à l’autre bout de la ligne. Selon la situation, la valeur associée à l’action « se trouver sur la ligne de tram » peut donc changer. Ce qui est possible en revanche, c’est de collecter de l’information sur la position du tram, par exemple en regardant sur l’application dédiée sur mon téléphone. L’information que j’obtiendrai ainsi ne sera pas absolument exacte (l’application peut avoir un léger décalage ou seulement donner le prochain arrêt par exemple) mais elle me permettra d’effectuer un raisonnement complexe, comme « le tram est 3 arrêts plus loin, je peux rester un peu sur la ligne sans danger, mais plus j’attends plus c’est dangereux ».
Il existe un modèle mathématique, basé sur la théorie des probabilités, qui permet de modéliser ce genre de problème, et qui s’appelle le Processus de Markov Partiellement Observable (POMDP de son petit nom, prononcez pom-dé-pé). Les POMDP permettent de modéliser tout ce qui peut se passer dans notre monde : les états possibles, les effets possibles des actions de l’agent ainsi que leur probabilité d’occurrence, et ce que l’agent reçoit comme information lorsqu’il effectue une action.
À partir de là, il existe de nombreux algorithmes qui permettent à un agent de raisonner sur l’ensemble des situations, de considérer les différentes actions possibles et de choisir la meilleure suite d’actions à effectuer en fonction de ce qu’il sait, de ce qu’il a vu du monde et afin d’atteindre son but. Par exemple, pour mon Cluedo, si je sais que j’ai la carte Salon dans la main, je ne vais généralement pas me déplacer dans le salon car je sais que ça ne fait pas partie de la solution. Néanmoins, l’une des limitations de ce modèle est que les valeurs ne peuvent être attribuées qu’à des états et des actions (par exemple : arriver chez le docteur). Or dans le cas de la recherche active d’information, le comportement désirable est celui qui permet à notre agent d’en apprendre le plus possible sur le monde. Il n’est donc pas lié à un état ou une action particulière mais à son état de connaissance : on aimerait récompenser l’agent s’il sait que le crime a eu lieu dans le salon. Peu importe si notre agent se trouve dans la cuisine ou la salle à manger et comment il le sait. L’important, c’est qu’il le sache. C’est cette limitation que les auteurs de l’article tentent de dépasser.
Actions d’Engagement : le Colonel Moutarde dans la cuisine avec le chandelier
Pour modéliser cette récompense basée sur l’état de connaissance d’un agent, les auteurs présentent un nouveau modèle basé sur les POMDP, qu’ils appellent POMDP-IR (pour POMDP with Information Reward ou POMDP avec récompense d’information en français). Dans ce nouveau modèle, les auteurs introduisent ce qu’ils appellent des actions d’engagement. Pour comprendre ce qu’est une action d’engagement, repensez au Cluedo. À la fin de la partie, lorsque vous avez obtenu assez d’information sur les différentes pièces, armes et suspect·e·s, vous êtes suffisamment sûr·e de vous pour émettre une accusation : « c’est le Colonel Moutarde dans la cuisine avec le chandelier ». Cette accusation est une action d’engagement : si vous avez raison, vous serez récompensé·e (vous gagnez la partie). Si vous avez tort, vous serez pénalisé·e (vous sortez du jeu). De ce fait, vous vous assurez d’avoir suffisamment d’information avant d’émettre votre accusation. Eh bien dans cet article, les auteurs ont créé des agents capables de jouer de Cluedo ! Grâce aux actions d’engagement, l’agent se focalise sur les actions qui lui permettent de récolter de l’information afin d’obtenir un état de connaissance suffisant avant de s’engager, et donc soit de recevoir une récompense (s’il a raison), soit d’être pénalisé (s’il a tort).
Mais nos agents POMDP-IR ne sont pas que des joueurs de Cluedo et peuvent faire bien plus. En effet, un POMDP-IR permet de modéliser, en parallèle des actions d’engagement, n’importe quelle autre action qui serait modélisable dans un POMDP. À chaque action, l’agent peut alors décider simultanément d’une action « normale » et de s’engager ou non. De ce fait, le POMDP-IR permet de modéliser des problèmes multi-objectifs, où l’agent doit mettre en œuvre sa perception active tout en poursuivant une autre mission. On peut imaginer par exemple le cas de missions de sauvetage où l’agent doit retrouver des victimes et sécuriser l’environnement. Sécuriser l’environnement est la mission « classique » (au sens des POMDP, car il s’agit de modifier l’état de l’environnement par les actions de l’agent), alors que retrouver les victimes est une mission de perception active (modélisable par un POMDP-IR), car on attend de l’agent qu’il prenne des actions d’engagement du type « je sais qu’il y a un blessé au troisième étage ».
Donc on peut maintenant récompenser un agent pour effectuer sa mission tout en ayant un état de connaissance suffisant. Mais, ça veut dire quoi suffisant ?
Les auteurs nous disent : suffisant, ça dépend du contexte ! Évidemment, ce que vous considérez comme étant un état de connaissance suffisant dépend énormément de votre application. S’il s’agit d’indiquer à l’utilisateur·rice que le café est prêt, les erreurs ne sont pas bien graves. Par contre s’il s’agit de secourir des victimes, une erreur pourrait vous coûter cher. Les auteurs démontrent également qu’à vouloir être trop sûr, l’agent risque de se focaliser sur sa recherche d’information, quitte à délaisser toute autre mission qui pourrait lui être confiée. Dans le cas de notre agent de sauvetage par exemple, si l’on demande à l’agent d’être trop sûr d’où se trouvent les victimes, notre agent va passer son temps à vérifier et re-vérifier chaque pièce en négligeant de sécuriser l’environnement, risquant ainsi la vie de ses coéquipiers.
Pourquoi ce modèle est-il intéressant ?
Dans le monde de la recherche en Intelligence Artificielle, produire un nouveau modèle ne suffit pas, encore faut-il qu’il soit intéressant. Alors comment détermine-t-on qu’un modèle est intéressant ? Souvent grâce à deux questions :
- Ce modèle permet-il de modéliser un type de problème qu’on ne savait pas traiter jusque là ? Si oui, il permet d’accroître le nombre de problèmes qu’un agent artificiel peut traiter et il est donc intéressant.
- Si d’autres modèles permettent déjà de modéliser le même type de problème que ce nouveau modèle, ce nouveau modèle est-il meilleur que l’ensemble des autres modèles existant ?
- Est-il plus simple à appliquer ?
- Donne-t-il de meilleurs résultats ?
Dans notre cas, le POMDP-IR introduit par Matthijs Spaan et ses collègues ne permet pas de modéliser de nouveaux problèmes car il existe déjà un autre modèle permettant de traiter le problème de la recherche active d’information. Ce modèle, appelé ![]() -POMDP, a été proposé cinq ans plus tôt (en 2010) par Mauricio Araya-Lopez et ses collègues [1]. D’après ses auteurs, le POMDP-IR permet de meilleurs résultats que le
-POMDP, a été proposé cinq ans plus tôt (en 2010) par Mauricio Araya-Lopez et ses collègues [1]. D’après ses auteurs, le POMDP-IR permet de meilleurs résultats que le ![]() -POMDP, au sens où un agent qui suivrait un POMDP-IR aura une meilleure récompense finale (et donc sera a priori plus efficace dans sa tâche) qu’un agent qui suivrait un
-POMDP, au sens où un agent qui suivrait un POMDP-IR aura une meilleure récompense finale (et donc sera a priori plus efficace dans sa tâche) qu’un agent qui suivrait un ![]() -POMDP.
-POMDP.
Conclusion et Discussion
Le modèle développé par les auteurs dans cet article permet à un agent de raisonner sur ses connaissances afin d’agir au mieux pour acquérir de nouvelles connaissances tout en poursuivant d’autres buts. Ce modèle se base essentiellement sur la notion d’actions d’engagement, qui permettent de récompenser l’agent lorsque celui-ci obtient un bon niveau de connaissance sur le monde.
L’une des difficultés majeures associées à ce modèle est de trouver le bon équilibre entre les différentes missions. C’est un aspect qui n’est pas du tout abordé dans l’article, mais qui est pourtant capital afin d’obtenir un comportement adéquat. En effet, dans le cas de notre agent de sauvetage, l’agent est récompensé s’il trouve les victimes correctement et s’engage sur leur position, mais également s’il sécurise au mieux l’environnement. La relation entre ces deux récompenses est tout aussi capitale que le degré de suffisant afin d’obtenir un agent qui effectue bien ses deux missions. Une récompense trop élevée pour la sécurisation de l’environnement par rapport à celle pour la recherche de victimes va inciter l’agent à prioriser la sécurisation et négliger la recherche des victimes, et inversement une récompense de sécurisation trop faible par rapport à la récompense de recherche de victime va inciter l’agent à négliger sa tâche de sécurisation. Ce problème n’est cependant pas propre au POMDP-IR, puisqu’il existe dans tout modèle la nécessité de trouver un compromis entre différents objectifs, ce qui implique malheureusement souvent une suite d’essais et d’erreurs afin de trouver la bonne configuration.
Le problème de raisonner et planifier sur l’état de connaissance d’un agent est un sujet qui suscite énormément d’intérêt dans la communauté de recherche sur la planification automatique. Ce (relativement) nouveau domaine de recherche est appelé Planification Épistémique et verra probablement émerger de nombreux modèles dans le futur, ouvrant ainsi la voie à beaucoup de nouvelles applications.
Note : l’autrice de ce papier-mâché est, au moment de son écriture, en collaboration avec les auteurs de la publication scientifique initiale. Cette collaboration a débuté après la parution de celle-ci.
[1] Araya-Lopez M., Buffet O., Thomas V., Charpillet F., A POMDP Extension with Belief-dependent Rewards. NIPS Proceedings, 2010. [Publication scientifique]
Écriture : Jennifer Renoux
Relecture scientifique : Cédric Buron et Vincent Thomas
Relecture de forme : Aurélien Didier et Alexandre Fauquette
Temps de lecture : environ 19 minutes.
Thématiques : Intelligence artificielle (Informatique et Sciences cognitives)
Publication originale : Spaan M., et al., Decision-theoretic planning under uncertainty with information rewards for active cooperative perception. Autonomous Agents and Multi-Agent Systems, 2014. DOI : 10.1007/s10458-014-9279-8

Les bons joueurs de Cluedo sont efficaces dans leur recherche d’information : ils planifient leurs actions afin d’obtenir le plus d’information possible en un minimum de temps. On appelle ce processus perception active, et c’est une capacité que les humains maîtrisent très bien. Pour les machines, en revanche, c’est plus compliqué. Dans un article de 2015, Matthijs Spaan, Tiago Veiga et Pedro U. Lima ont proposé un modèle dotant les machines de capacités de perception active, avec des applications dans le domaine de la robotique autonome pour la surveillance ou le sauvetage de personnes.
Perception active et Planification sous incertitude. Kesako ?
En tant qu’humain, lorsque que l’on marche dans la rue, on absorbe de l’information sur ce qui se passe autour de nous : le feu piéton au vert, le tram qui arrive en station ou le fait que l’on vient d’arriver sur l’avenue Jean Capelle et que le bâtiment où l’on va se trouve droit devant nous. Ces informations sont intégrées par notre cerveau presque inconsciemment pendant qu’il est occupé à planifier la prochaine action pour nous amener à notre but final : notre rendez-vous chez le docteur. Dans le monde de la planification automatique [1], la plupart des problèmes considérés suivent ce schéma : l’agent artificiel (souvent abrégé en agent) calcule un plan lui permettant d’accomplir sa mission, et l’information qu’il obtient lors de l’exécution de ce plan est au service de la mission. La recherche d’information est alors un moyen pour atteindre un but et non le but en lui-même. Cependant, il existe certains cas d’applications où la recherche d’information n’est pas seulement un moyen pour l’agent d’atteindre un but mais constitue le but en lui-même. C’est par exemple le cas dans des applications de surveillance et de patrouille, mais aussi de recherche et de sauvetage, où la vie de personnes dépend de notre capacité à collecter de l’information vite et bien.
Ce processus s’appelle la Recherche active d’information, ou Perception Active. Le but ici est de collecter le plus possible d’information à propos de certains points d’intérêts. Pensez notamment à une partie de Cluedo, où il vous faut trouver le coupable, l’arme et le lieu du crime. Vous devez donc vous déplacer dans l’environnement et récolter de l’information afin d’éliminer les suspect·e·s, armes, et lieux potentiels.
Pour un humain, la perception active est simple. On la pratique depuis qu’on est gamin·e, quand on cherche nos clefs ou qu’on tente de se retrouver après s’être perdu·e. On est entraîné·e. Mais comme souvent dans le domaine de l’IA (Intelligence Artificielle), ce qui est facile pour un humain peut être très compliqué pour un agent artificiel et demande un effort de recherche important de la part de la communauté scientifique. Alors, comment on fait ?
La perception active se fonde presque toujours sur un modèle de connaissance de l’agent : il faut que l’on soit capable de modéliser ce dont l’agent est certain, mais également ce dont il est incertain. Dans cet article, les auteurs se placent dans le cadre de la planification sous incertitude basée sur la théorie de la décision. La planification sous incertitude, c’est quoi au juste ? C’est quand un agent doit être capable de calculer les meilleures actions possibles alors qu’il n’a qu’une connaissance partielle et/ou imprécise du monde qui l’entoure. Dans votre partie de Cluedo, vous allez tenter de trouver la meilleure suite d’actions et d’annonces pour trouver le coupable le plus rapidement possible. Encore une fois, pour les humains, facile, on la pratique tous les jours ! Pour les IA, c’est plus compliqué. La théorie de la décision (dans notre cas) signifie que l’on va attribuer une valeur, aussi appelée utilité, à certains états (par exemple l’état « je suis arrivée chez le docteur »), certaines actions (par exemple l’action « je tourne à gauche après le tram »), et que le but de l’agent va être de maximiser son utilité espérée, c’est à dire la somme des utilités de chaque état qu’il va traverser et actions qu’il va prendre.
Afin d’illustrer le modèle décrit dans l’article, commençons par l’exemple des auteurs : celui de la patrouille, illustré par la Figure 1.
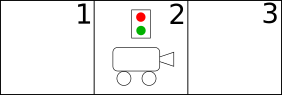
Dans cet exemple, notre robot doit combiner deux objectifs : patrouiller le corridor et surveiller l’alarme. Aucun de ces deux objectifs ne doit être négligé.
Les auteurs de l’article se placent dans le cadre des Processus de Markov Partiellement Observables, ou POMDP (prononcez : pom-dé-pé). Dans le reste de cette partie, on va voir ensemble les bases des POMDP, qui sont indispensables pour comprendre le reste de l’article. Pas besoin de tout comprendre en détails, les grandes lignes suffisent. Mais si vous êtes déjà familiers des POMDP, vous pouvez sauter à la prochaine section !
Un POMDP permet de modéliser un problème pour lequel un agent doit prendre un certain nombre de décisions (= effectuer des actions) séquentiellement (= les unes après les autres). Pour ce faire, le POMDP modélise la structure du monde (c’est à dire les points d’intérêts, les états possibles, etc.) ainsi que son évolution (comment le monde passe d’un état à l’autre), les capacités de l’agent, ce qu’il observe du monde, ainsi que son but.
Dans un POMDP, on considère que le monde évolue de manière stochastique. Cela signifie qu’effectuer une action donnée dans un état du monde donné ne produira pas toujours le même résultat. Par exemple, pour le problème de la patrouille, si le robot effectue l’action « aller à droite » alors qu’il est dans l’état « position 1 », il est fort probable qu’il finisse dans l’état « position 2 ». Cependant, si pour une quelconque raison, ses moteurs ne fonctionnent pas correctement, il se peut qu’il reste dans l’état « position 1 ». L’une des forces majeures des POMDP est qu’ils permettent de modéliser l’ensemble des évènements possibles en prenant en compte leur probabilité d’occurrence, ce qui permet ainsi à l’agent de raisonner sur les différents scénarios possibles.
Formellement, un POMDP se compose de 6 éléments, notés <![]() > :
> :
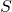 est l’ensemble des états possibles du monde. Dans ce cas de la patrouille, l’état est défini par la couleur de l’alarme (verte ou rouge), la position du robot (position 1, 2 ou 3) et l’extrémité du corridor vers laquelle le robot doit se diriger (position 1 ou 3). Cette dernière variable permet de forcer l’agent à patrouiller le corridor en changeant de côté lorsque le robot atteint l’une des extrémités du corridor.
est l’ensemble des états possibles du monde. Dans ce cas de la patrouille, l’état est défini par la couleur de l’alarme (verte ou rouge), la position du robot (position 1, 2 ou 3) et l’extrémité du corridor vers laquelle le robot doit se diriger (position 1 ou 3). Cette dernière variable permet de forcer l’agent à patrouiller le corridor en changeant de côté lorsque le robot atteint l’une des extrémités du corridor.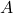 est l’ensemble des actions possibles de l’agent. Dans le cas de la patrouille, le robot peut : « aller à gauche », « aller à droite », ou « regarder l’alarme ».
est l’ensemble des actions possibles de l’agent. Dans le cas de la patrouille, le robot peut : « aller à gauche », « aller à droite », ou « regarder l’alarme ».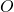 est l’ensemble des observations possibles que l’agent peut obtenir. Dans le cas de la patrouille, le robot peut observer la couleur de l’alarme ainsi que la position dans laquelle il se trouve.
est l’ensemble des observations possibles que l’agent peut obtenir. Dans le cas de la patrouille, le robot peut observer la couleur de l’alarme ainsi que la position dans laquelle il se trouve.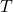 est la fonction de transition. Elle représente la façon dont le monde évolue en fonction des décisions prises par l’agent. C’est elle qui représente le fait que certaines actions peuvent avoir des résultats différents et permet de modéliser l’intégralité des évènements possibles. En pratique, c’est une distribution de probabilité qui définit la probabilité conditionnelle que le monde évolue d’un état
est la fonction de transition. Elle représente la façon dont le monde évolue en fonction des décisions prises par l’agent. C’est elle qui représente le fait que certaines actions peuvent avoir des résultats différents et permet de modéliser l’intégralité des évènements possibles. En pratique, c’est une distribution de probabilité qui définit la probabilité conditionnelle que le monde évolue d’un état 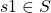 vers un état
vers un état 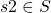 sachant que l’agent a effectué l’action
sachant que l’agent a effectué l’action 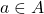 . Cette distribution de probabilité s’écrit
. Cette distribution de probabilité s’écrit 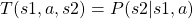 . Dans le cas de la patrouille,
. Dans le cas de la patrouille, 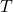 pourra modéliser par exemple le fait que le moteur peut parfois se retrouver en panne, et donc le robot reste à sa place alors qu’il essaye d’avancer.
pourra modéliser par exemple le fait que le moteur peut parfois se retrouver en panne, et donc le robot reste à sa place alors qu’il essaye d’avancer.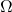 est la fonction d’observation. Elle a une forme similaire à la fonction de transition et définit la probabilité conditionnelle que l’agent reçoive une observation
est la fonction d’observation. Elle a une forme similaire à la fonction de transition et définit la probabilité conditionnelle que l’agent reçoive une observation 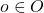 donnée sachant l’état du monde
donnée sachant l’état du monde 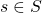 et l’action
et l’action 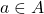 effectuée par l’agent :
effectuée par l’agent : 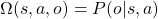 . Dans l’exemple de la patrouille, cette fonction permet par exemple de représenter l’incertitude sur les résultats des capteurs du robot : le robot peut observer que l’alarme est rouge alors qu’elle est verte, ou inversement, si sa caméra ne fonctionne pas bien.
. Dans l’exemple de la patrouille, cette fonction permet par exemple de représenter l’incertitude sur les résultats des capteurs du robot : le robot peut observer que l’alarme est rouge alors qu’elle est verte, ou inversement, si sa caméra ne fonctionne pas bien. 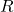 est la fonction de récompense. C’est elle qui permet de définir le but de l’agent.
est la fonction de récompense. C’est elle qui permet de définir le but de l’agent. 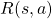 est un réel et définit la récompense immédiate que l’agent obtient s’il effectue l’action
est un réel et définit la récompense immédiate que l’agent obtient s’il effectue l’action  dans l’état
dans l’état  .
.
Une fois que l’on a modélisé notre problème avec notre POMDP, il est temps de déterminer quelle action l’agent doit effectuer dans quelle situation. Ce processus s’appelle la planification et consiste à calculer une politique optimale. C’est-à-dire déterminer la meilleure action à effectuer pour chaque état possible. Le seul problème, c’est que dans le cas des POMDP l’agent ne sait pas exactement dans quel état il est. Il n’a accès qu’à des observations incomplètes et potentiellement erronées. Comme on ne peut pas prendre les observations pour argent comptant, on va maintenir ce que l’on appelle un état de croyance.
L’état de croyance d’un agent représente, pour cet agent, les chances que le monde soit dans un état donné en fonction de ce qu’il a fait et observé précédemment. Si l’on prend encore l’exemple de la patrouille et que l’agent sait qu’il a effectué l’action « aller à droite », suivie de « regarder l’alarme » et qu’il a obtenu l’observation « l’alarme est rouge », alors il est probable que l’agent soit en position 2 et que l’alarme soit effectivement rouge. En revanche, si après la même suite d’actions l’agent observe « pas d’alarme », alors il est probable qu’il soit en position 3. L’état de croyance modélise donc un résumé des actions précédemment effectuées et des observations précédemment reçues. Formellement, l’état de croyance est une distribution de probabilité sur l’ensemble des états ![]() , qui donne pour chaque
, qui donne pour chaque ![]() la probabilité selon l’agent que le monde soit effectivement dans l’état
la probabilité selon l’agent que le monde soit effectivement dans l’état ![]() . Notre politique optimale va se baser sur cet état de croyance au lieu de l’état réel du monde auquel l’agent n’a de toute façon pas accès. Pour notre agent patrouilleur, cela revient à dire que s’il croit très fortement être en position 3 (= la probabilité est supérieure à un certain seuil) et que l’extrémité à rejoindre se trouve en position 1, alors la meilleure action à effectuer est d’aller à gauche. D’un point de vue mathématique, ça veut dire que notre politique optimale est une application de l’espace des états de croyance dans l’espace des actions et nous donne pour chaque état de croyance la meilleure action possible. Par exemple, la Figure 2 représente une politique possible pour la patrouille.
. Notre politique optimale va se baser sur cet état de croyance au lieu de l’état réel du monde auquel l’agent n’a de toute façon pas accès. Pour notre agent patrouilleur, cela revient à dire que s’il croit très fortement être en position 3 (= la probabilité est supérieure à un certain seuil) et que l’extrémité à rejoindre se trouve en position 1, alors la meilleure action à effectuer est d’aller à gauche. D’un point de vue mathématique, ça veut dire que notre politique optimale est une application de l’espace des états de croyance dans l’espace des actions et nous donne pour chaque état de croyance la meilleure action possible. Par exemple, la Figure 2 représente une politique possible pour la patrouille.

Et normalement, les lecteurs et lectrices avertis diront « Mais Jamy, l’état de croyance étant une distribution de probabilité, l’espace des états de croyance est continu et donc c’est galère pour définir la politique ! ». Je répondrai que oui Fred, c’est galère, mais on a des moyens de gérer ça ! On ne rentrera pas plus dans les détails du comment ici, on n’a pas le temps. Si vous êtes intéressé·es, vous pouvez vous référer au tutorial sur les POMDP de Anthony Cassandra pour une introduction en la matière (en anglais).
Bon, on en a presque fini avec les notions de base et on a fait le plus dur. Il nous reste un tout petit truc à voir concernant l’espace d’états ![]() . Comme on l’a déjà dit, il représente l’ensemble des états possibles du monde. Dans notre exemple, un état possible c’est « alarme rouge, robot en position 1, et extrémité à rejoindre en position 3 ». Un autre état possible : « alarme rouge, robot en position 2, et extrémité à rejoindre en position 1 ». Un autre : « alarme verte, robot en position 1, et extrémité à rejoindre en position 3 ». Et ainsi de suite. On se rend rapidement compte qu’avec une telle construction, le nombre d’états possibles va grandir exponentiellement avec le nombre de propriétés considérées (la position du robot, la couleur de l’alarme, etc.). En réalité, lorsque l’on décrit le monde, on opte souvent pour une représentation factorisée : on définit plusieurs variables d’état dont la combinaison nous donne un état possible du monde. Naturellement, dans notre exemple, la couleur de l’alarme est une variable d’état dont les valeurs possibles sont « rouge » et « verte ». La position du robot est une autre variable d’état et ses valeurs possibles sont 1, 2 et 3. L’extrémité du corridor à rejoindre est une troisième variable dont les valeurs possibles sont 1 et 3.
. Comme on l’a déjà dit, il représente l’ensemble des états possibles du monde. Dans notre exemple, un état possible c’est « alarme rouge, robot en position 1, et extrémité à rejoindre en position 3 ». Un autre état possible : « alarme rouge, robot en position 2, et extrémité à rejoindre en position 1 ». Un autre : « alarme verte, robot en position 1, et extrémité à rejoindre en position 3 ». Et ainsi de suite. On se rend rapidement compte qu’avec une telle construction, le nombre d’états possibles va grandir exponentiellement avec le nombre de propriétés considérées (la position du robot, la couleur de l’alarme, etc.). En réalité, lorsque l’on décrit le monde, on opte souvent pour une représentation factorisée : on définit plusieurs variables d’état dont la combinaison nous donne un état possible du monde. Naturellement, dans notre exemple, la couleur de l’alarme est une variable d’état dont les valeurs possibles sont « rouge » et « verte ». La position du robot est une autre variable d’état et ses valeurs possibles sont 1, 2 et 3. L’extrémité du corridor à rejoindre est une troisième variable dont les valeurs possibles sont 1 et 3.
Vous êtes encore là ? Super ! Et si on rentrait dans les détails du papier maintenant ? On a les bases, le plus intéressant reste à venir.
Un POMDP étendu pour raisonner sur les croyances
Le but de ce modèle, on l’a évoqué, est de faire de la perception active, c’est à dire de récolter de l’information. L’agent doit donc être capable de raisonner à propos de ce qu’il sait et de ce qu’il sait ne pas savoir. Pour cela, les auteurs introduisent la notion de récompense basée sur l’information. On l’a dit précédemment, dans un POMDP classique, l’agent reçoit une récompense lorsqu’il atteint un état donné. Sauf que pour la recherche d’information, ça ne marche plus ! En effet, dans ce cas, on ne cherche pas à ce que l’agent atteigne un certain état mais à ce qu’il soit sûr de ce qu’il croit.
Ce problème a été très étudié par la communauté scientifique entre 2010 et 2015. En 2010, Mauricio Araya-Lopez et ses collègues ont présenté le modèle ![]() -POMDP, une extension des POMDP qui permet de récompenser un agent sur la base de son état de croyance [2]. Cette extension, encore très utilisée aujourd’hui, présente néanmoins un inconvénient : les algorithmes classiques utilisés pour faire de la planification dans les POMDP ne s’appliquent pas au
-POMDP, une extension des POMDP qui permet de récompenser un agent sur la base de son état de croyance [2]. Cette extension, encore très utilisée aujourd’hui, présente néanmoins un inconvénient : les algorithmes classiques utilisés pour faire de la planification dans les POMDP ne s’appliquent pas au ![]() -POMDP. Matthijs Spaan et ses collègues, les auteurs de l’article qui nous intéresse ici, ont évité cet écueil et présentent une extension qui reste dans le cadre des POMDP et donc permet l’utilisation des (nombreux) algorithmes de planification déjà existants. Comment ont-ils fait ?
-POMDP. Matthijs Spaan et ses collègues, les auteurs de l’article qui nous intéresse ici, ont évité cet écueil et présentent une extension qui reste dans le cadre des POMDP et donc permet l’utilisation des (nombreux) algorithmes de planification déjà existants. Comment ont-ils fait ?
Les auteurs ont défini le cadre POMDP-IR (POMDP with Information Reward = POMDP avec récompense d’information) en introduisant un certain type d’action dans l’espace d’action ![]() , qu’ils appellent action d’engagement (commit en anglais). Ils considèrent que, parmi l’intégralité des variables d’états d’un POMDP, on n’est intéressé que par un sous-ensemble d’entre-elles, qui sont appelées variables d’intérêt. À chaque étape, notre agent POMDP-IR devra choisir simultanément une action de domaine (aller à gauche, à droite, ou regarder l’alarme), et pour chaque variable d’intérêt, choisir s’il s’engage ou non sur la valeur de cette variable. S’engager sur la valeur d’une variable d’intérêt signifie pour l’agent qu’il est suffisamment sûr de la valeur de cette variable à ce moment. Repensez au Cluedo. À la fin de la partie, lorsque vous avez obtenu assez d’informations sur les différentes pièces, armes et suspect·e·s, vous êtes suffisamment sûr·e·s de vous pour émettre une accusation : c’est le Colonel Moutarde dans la cuisine avec le chandelier !
, qu’ils appellent action d’engagement (commit en anglais). Ils considèrent que, parmi l’intégralité des variables d’états d’un POMDP, on n’est intéressé que par un sous-ensemble d’entre-elles, qui sont appelées variables d’intérêt. À chaque étape, notre agent POMDP-IR devra choisir simultanément une action de domaine (aller à gauche, à droite, ou regarder l’alarme), et pour chaque variable d’intérêt, choisir s’il s’engage ou non sur la valeur de cette variable. S’engager sur la valeur d’une variable d’intérêt signifie pour l’agent qu’il est suffisamment sûr de la valeur de cette variable à ce moment. Repensez au Cluedo. À la fin de la partie, lorsque vous avez obtenu assez d’informations sur les différentes pièces, armes et suspect·e·s, vous êtes suffisamment sûr·e·s de vous pour émettre une accusation : c’est le Colonel Moutarde dans la cuisine avec le chandelier !
Mathématiquement, cela se traduit par le fait que sa croyance sur cette variable d’intérêt dépasse un certain seuil fixé par le problème. Par exemple, dans le cadre de la patrouille, on souhaite être certain du fait que l’alarme soit rouge et on va donc s’attendre à ce que la probabilité, selon l’agent, que l’alarme soit rouge dépasse 0,9. Évidemment, l’agent est récompensé s’il a raison (on appellera la valeur reçue ![]() , avec
, avec ![]() ) et pénalisé s’il a tort (la valeur reçue est
) et pénalisé s’il a tort (la valeur reçue est ![]() , avec
, avec ![]() )
)
Alors, dans le cas de la patrouille, ça nous donne quoi ? Nous avons les actions de domaine classiques déjà évoquées (aller à gauche, aller à droite, regarder l’alarme) auxquelles s’ajoute une action d’engagement qu’on appellera « engagement Alarme Rouge », que l’agent devra prendre pour s’engager sur le fait que l’alarme soit rouge. Maintenant, le problème est de définir les récompenses de façon à ce que l’agent s’engage lorsque sa croyance est « suffisamment bonne », c’est-à-dire que « la probabilité selon l’agent que l’alarme soit rouge est supérieure à un seuil donné ». Pour l’exemple, on prendra le seuil à 0,75. Mais comment choisir une récompense appropriée ?
Les auteurs nous disent que le plus important dans ce cas est la relation entre ![]() et
et ![]() , et non pas les valeurs exactes. En effet, ce que l’on souhaite, c’est que l’agent soit récompensé et pénalisé juste assez pour ne choisir l’action « engagement Alarme Rouge » que si sa croyance dans le fait que l’alarme soit rouge est supérieure à notre seuil (dans notre exemple 0,75). Et les auteurs ont été suffisamment sympas pour nous donner une équation définissant cette relation en fonction du seuil de croyance choisi. Cette équation, là voici :
, et non pas les valeurs exactes. En effet, ce que l’on souhaite, c’est que l’agent soit récompensé et pénalisé juste assez pour ne choisir l’action « engagement Alarme Rouge » que si sa croyance dans le fait que l’alarme soit rouge est supérieure à notre seuil (dans notre exemple 0,75). Et les auteurs ont été suffisamment sympas pour nous donner une équation définissant cette relation en fonction du seuil de croyance choisi. Cette équation, là voici :
![]()
Si l’on applique donc cette équation à notre exemple de la patrouille, disons que l’on choisit un ![]() (choix totalement arbitraire), et un seuil
(choix totalement arbitraire), et un seuil ![]() 0,75, alors l’équation nous dit que l’on doit utiliser
0,75, alors l’équation nous dit que l’on doit utiliser ![]() 3,33.
3,33.
Maintenant, on sait comment choisir la récompense appropriée, en fonction d’un seuil ![]() voulu. Mais comment choisir
voulu. Mais comment choisir ![]() ?
?
Les auteurs nous disent : ça dépend du contexte. Évidemment, ce que vous considérez comme étant une croyance suffisante dépendra énormément de votre application. S’il s’agit d’indiquer à l’utilisateur que le café est prêt, les erreurs ne sont pas bien graves. Par contre s’il s’agit d’activer automatiquement les arroseurs parce qu’un départ de feu a été détecté dans la salle des serveurs, une erreur pourrait vous coûter cher ! Et on parle ici en réalité de deux types d’erreur possible :
- L’agent pense qu’il n’y a pas de feu et ne déclenche pas les arroseurs. Or il y avait un feu, et tout a brûlé (c’est ce qu’on appelle un faux négatif).
- L’agent pense qu’il y a un feu et déclenche les arroseurs. Or il n’y avait pas de feu, et tout est trempé (c’est ce qu’on appelle un faux positif).
Dans les deux cas, l’erreur a de graves conséquences et on préférerait être sûrs avant d’agir. Du coup, on aimerait un ![]() élevé.
élevé.
Par contre, choisir un ![]() trop élevé pourrait amener votre robot à fixer l’alarme sans relâche pour être absolument sûr de ne rien manquer, au détriment de son autre mission : patrouiller le corridor. Pire, si votre seuil
trop élevé pourrait amener votre robot à fixer l’alarme sans relâche pour être absolument sûr de ne rien manquer, au détriment de son autre mission : patrouiller le corridor. Pire, si votre seuil ![]() est si élevé qu’il est mathématiquement inatteignable, le robot se contentera de patrouiller dans le couloir sans s’occuper de son alarme. Après tout, pourquoi s’enquiquiner à essayer de faire quelque chose que vous savez d’avance être impossible ?!
est si élevé qu’il est mathématiquement inatteignable, le robot se contentera de patrouiller dans le couloir sans s’occuper de son alarme. Après tout, pourquoi s’enquiquiner à essayer de faire quelque chose que vous savez d’avance être impossible ?!
Expérience #1 : impact de 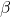
Dans une première expérience sur le problème de la patrouille, les auteurs ont étudié l’impact du ![]() sur le comportement de l’agent. Ils ont choisi trois valeurs différentes de
sur le comportement de l’agent. Ils ont choisi trois valeurs différentes de ![]() (0,75 ; 0,9 ; 0,99) et ont étudié comment cette valeur impactait le comportement global de l’agent dans le problème de la patrouille. Ils ont montré dans un premier temps qu’avec
(0,75 ; 0,9 ; 0,99) et ont étudié comment cette valeur impactait le comportement global de l’agent dans le problème de la patrouille. Ils ont montré dans un premier temps qu’avec ![]() 0,75 l’agent patrouille correctement son environnement et poursuit ses deux buts en parallèle : il alterne entre les positions 1, 2 et 3, s’arrête régulièrement en position 2 pour regarder l’alarme, choisi son action d’engagement correctement, puis reprend sa patrouille.
0,75 l’agent patrouille correctement son environnement et poursuit ses deux buts en parallèle : il alterne entre les positions 1, 2 et 3, s’arrête régulièrement en position 2 pour regarder l’alarme, choisi son action d’engagement correctement, puis reprend sa patrouille.
Dans le second cas, avec ![]() 0,9, ils montrent que lorsque l’agent arrive en position 2, il reste en position 2 et regarde l’alarme pendant une période de temps prolongée, négligeant sa patrouille. La différence entre ces deux comportements vient du fait qu’il est mathématiquement possible pour l’agent d’obtenir une croyance supérieure à 0,9, mais cela nécessite des observations répétées et successives. Dès que l’agent cesse de regarder l’alarme, sa croyance va diminuer (car l’environnement est dynamique et l’alarme peut avoir changé de couleur sans que le robot ne le voit) et passer en dessous du seuil voulu. Ainsi le robot reste immobile à fixer l’alarme.
0,9, ils montrent que lorsque l’agent arrive en position 2, il reste en position 2 et regarde l’alarme pendant une période de temps prolongée, négligeant sa patrouille. La différence entre ces deux comportements vient du fait qu’il est mathématiquement possible pour l’agent d’obtenir une croyance supérieure à 0,9, mais cela nécessite des observations répétées et successives. Dès que l’agent cesse de regarder l’alarme, sa croyance va diminuer (car l’environnement est dynamique et l’alarme peut avoir changé de couleur sans que le robot ne le voit) et passer en dessous du seuil voulu. Ainsi le robot reste immobile à fixer l’alarme.
Dans le troisième cas, où ![]() 0,99, l’agent néglige complètement de regarder l’alarme et n’effectue que sa patrouille sans jamais s’arrêter en position 2. Ceci est dû au fait qu’il est mathématiquement impossible pour l’agent d’obtenir une croyance supérieure à 0,99 (ce que l’agent sait car il peut raisonner sur l’ensemble des situations possibles), et donc l’action d’engagement sera toujours trop risquée à prendre : l’agent estime qu’il sera trop pénalisé. En conclusion, il se focalise sur ce qu’il peut faire : la patrouille.
0,99, l’agent néglige complètement de regarder l’alarme et n’effectue que sa patrouille sans jamais s’arrêter en position 2. Ceci est dû au fait qu’il est mathématiquement impossible pour l’agent d’obtenir une croyance supérieure à 0,99 (ce que l’agent sait car il peut raisonner sur l’ensemble des situations possibles), et donc l’action d’engagement sera toujours trop risquée à prendre : l’agent estime qu’il sera trop pénalisé. En conclusion, il se focalise sur ce qu’il peut faire : la patrouille.
Expérience #2 : Comparaison avec le ρ-POMDP
Dans une seconde expérience, les auteurs comparent leur modèle POMDP-IR avec le ![]() -POMDP de Mauricio Araya-Lopez et ses collègues, que nous avons déjà évoqué plus haut. Le but de cette comparaison est d’étudier comment le POMDP-IR et
-POMDP de Mauricio Araya-Lopez et ses collègues, que nous avons déjà évoqué plus haut. Le but de cette comparaison est d’étudier comment le POMDP-IR et ![]() -POMDP diffèrent : quels problèmes peuvent être modélisés par les deux approches ? Est-il plus facile de trouver une politique optimale dans l’un des deux modèles ? Les politiques calculées sont-elles équivalentes ? etc.
-POMDP diffèrent : quels problèmes peuvent être modélisés par les deux approches ? Est-il plus facile de trouver une politique optimale dans l’un des deux modèles ? Les politiques calculées sont-elles équivalentes ? etc.
Ce type de comparaisons expérimentales est particulièrement important puisqu’un nouveau modèle sera généralement considéré intéressant s’il permet de modéliser un type de problème qui ne pouvait pas être modélisé jusque là, ou s’il est meilleur que les autres modèles existants. Un modèle étant en général considéré meilleur qu’un autre s’il est plus simple à résoudre ou si la politique qui en découle apporte une plus forte récompense.
Dans le cas de ![]() -POMDP et POMDP-IR, les auteurs argumentent que le POMDP-IR permet de facilement modéliser des problèmes multi-objectifs, dans lesquels un agent doit considérer plusieurs buts. Bien que ce genre de problème soit modélisable à l’aide d’un
-POMDP et POMDP-IR, les auteurs argumentent que le POMDP-IR permet de facilement modéliser des problèmes multi-objectifs, dans lesquels un agent doit considérer plusieurs buts. Bien que ce genre de problème soit modélisable à l’aide d’un ![]() -POMDP, cette modélisation peut être plus difficile que dans le cadre des POMDP-IR. Les auteurs montrent également que le POMDP-IR est meilleur que le
-POMDP, cette modélisation peut être plus difficile que dans le cadre des POMDP-IR. Les auteurs montrent également que le POMDP-IR est meilleur que le ![]() -POMDP même dans le cas où la recherche d’informations est le seul but recherché.
-POMDP même dans le cas où la recherche d’informations est le seul but recherché.
Conclusion et Discussion
L’approche développée par les auteurs dans cet article permet à un agent de raisonner sur ses connaissances afin d’agir au mieux pour acquérir de nouvelles connaissances tout en poursuivant d’autres buts. Ce modèle, comme tous les POMDP et extensions, souffre d’un problème de mise à l’échelle : il devient souvent impossible de calculer une politique efficace (ne parlons même pas de politique optimale) pour des problèmes réels. En effet, le problème de la patrouille est ce qu’on appelle un problème jouet : il a très peu d’états et très peu d’actions. Ce type de problème est très utile pour étudier le comportement d’un modèle et montrer que ce modèle est fonctionnel, mais c’est un problème bien moins complexe que les problèmes réels.
Une autre difficulté associée à ce modèle est de trouver le bon équilibre entre les différentes missions. C’est un aspect qui n’est pas du tout abordé dans l’article, mais qui est pourtant capital afin d’obtenir un comportement adéquat. En effet, dans le problème de la patrouille, l’agent est récompensé s’il effectue son action d’engagement correctement (il dit que l’alarme est rouge quand elle est réellement rouge), mais également lorsqu’il atteint l’une des extrémités du corridor (c’est à dire qu’il effectue sa patrouille correctement). La relation entre ces deux récompenses est tout aussi capitale que la valeur de ![]() afin d’obtenir un agent qui effectue bien ses deux missions. Une récompense trop élevée pour la patrouille par rapport à celle pour les actions d’engagement va inciter l’agent à prioriser la patrouille et négliger de regarder l’alarme, et inversement une récompense de patrouille trop faible par rapport à la récompense d’engagement va inciter l’agent à négliger sa patrouille. Ce problème n’est cependant pas propre au POMDP-IR mais existe pour tous modèle multi-objectifs, et nécessite malheureusement souvent une suite d’essais et d’erreurs afin de trouver la bonne configuration.
afin d’obtenir un agent qui effectue bien ses deux missions. Une récompense trop élevée pour la patrouille par rapport à celle pour les actions d’engagement va inciter l’agent à prioriser la patrouille et négliger de regarder l’alarme, et inversement une récompense de patrouille trop faible par rapport à la récompense d’engagement va inciter l’agent à négliger sa patrouille. Ce problème n’est cependant pas propre au POMDP-IR mais existe pour tous modèle multi-objectifs, et nécessite malheureusement souvent une suite d’essais et d’erreurs afin de trouver la bonne configuration.
Le problème de raisonner et planifier sur l’état de connaissance d’un agent autant que sur son état dans le monde est un sujet qui monte énormément dans la communauté. Ce (relativement) nouveau domaine de recherche est appelé Planning Épistémique et verra probablement émerger de nombreux modèles dans le futur, ouvrant ainsi la voie à beaucoup de nouveaux types d’applications.
Note : l’autrice de ce papier-mâché est, au moment de son écriture, en collaboration avec les auteurs de la publication scientifique initiale. Cette collaboration a débuté après la parution de celle-ci.
[1] C’est à dire le domaine de recherche qui cherche à permettre à des agents artificiel de raisonner sur leurs futures actions pour mieux les planifier (https://fr.wikipedia.org/wiki/Planification_(intelligence_artificielle))
[2] Araya-Lopez M., Buffet O., Thomas V., Charpillet F., A POMDP Extension with Belief-dependent Rewards. NIPS Proceedings, 2010. [Publication scientifique]