Les horloges atomiques de poche

Chargement de l'article...

Écriture : Grégory Gredat
Relecture scientifique : Léo Mangeolle
Relecture de forme : Jérémy Ferrand et Eléonore Bellot

Temps de lecture : environ 12 minutes.
Thématiques : Photonique (Physique)

Publication originale : Knappe S., et al., A microfabricated atomic clock. Applied Physics Letters, 2004. DOI : 10.1063/1.1787942

Dessin personnel, d’après *La persistance de la mémoire* aussi appelée *Les montres molles*, œuvre de Salvador Dali, 1931.

De plus en plus d’applications requièrent des références de temps performantes, que ce soit les systèmes de navigation par satellite, les réseaux de communications, les réseaux électriques intelligents, les radars météo, les réseaux de transactions financières, les véhicules autonomes, etc. Les horloges atomiques permettent d’atteindre une stabilité inégalée mais, très souvent, au détriment du volume qu’elles occupent. Difficile d’imaginer l’utilité d’une horloge de la taille d’un studio pour une application aux communications militaires sur le terrain ou dans un système embarqué de véhicule. À moins de trouver une solution pour que ces horloges tiennent dans la poche !

Une brève histoire du temps et de sa mesure

Avant de relater la prouesse technologique accomplie par S. Knappe et ses collègues au National Institute of Standards and Technology (NIST), laboratoire gouvernemental des États-Unis, quelques mots sur les horloges atomiques sont nécessaires.

Depuis la 13^e conférence générale des poids et mesures en 1967, la définition de l’unité du système international pour la mesure du temps, la seconde, repose sur une interaction entre la lumière et la matière spécifique aux atomes de césium.

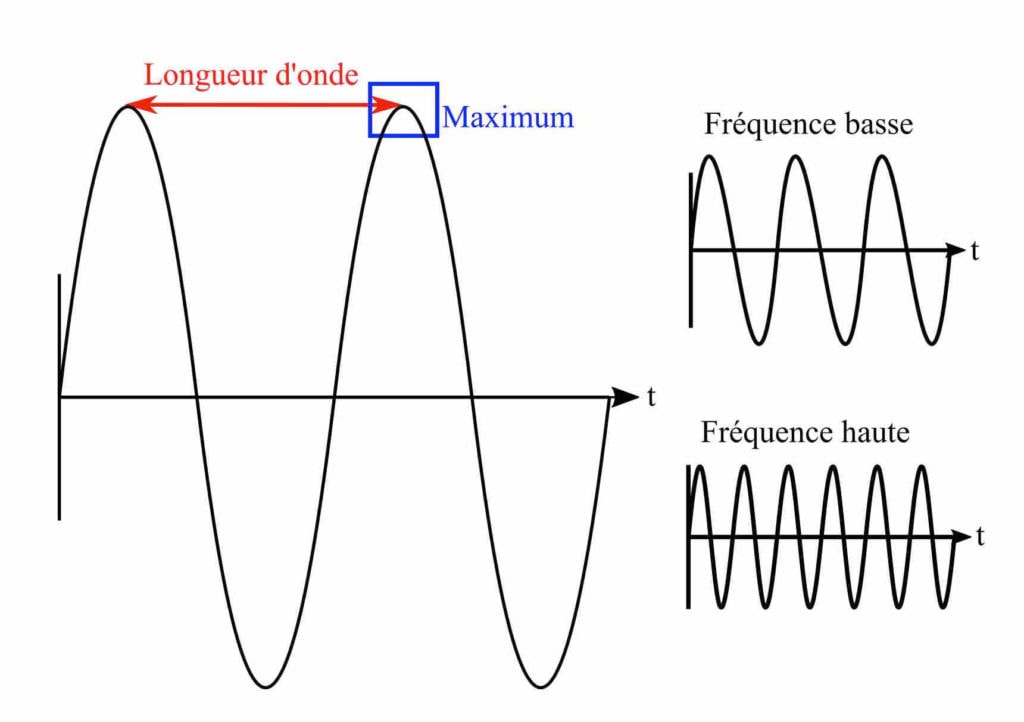
Courbe en forme de vague. Si les pics des vagues sont proches : fréquence haute, si elles sont plus éloignées: fréquence basse. — **Figure 1. Longueur et fréquence d’une onde sinusoïdale.** La longueur d’onde (en mètre) est la distance qui sépare deux maxima consécutifs d’une onde sinusoïdale tracée en fonction du temps. La fréquence (en hertz) d’une onde correspond au nombre de répétitions à l’identique par unité de temps de l’onde lors de sa propagation. Plus la fréquence est élevée, plus la distance entre deux maxima consécutifs est petite.

La valeur de la fréquence de l’onde de lumière associée à cette interaction spécifique est fixée à exactement 9 192 631 770 hertz (9,2 GHz). C’est-à-dire qu’une fois comptés exactement 9 192 631 770 passages consécutifs par un maximum de l’onde lumineuse au cours de sa propagation, une seconde s’est alors précisément écoulée (voir Figures 1 et 2).

Flèche qui indique la fréquence, en hertz, croissante. L'onde a des vagues plus serrées à mesure que la fréquence augmente. La longueur d'onde est plus haute pour une basse fréquence et plus basse pour une haute fréquence. — **Figure 2. Les différents domaines des ondes électromagnétiques selon leur fréquence / leur longueur d’onde.** IR : infrarouge ; UV : ultraviolet. Les rayonnements visibles se situent dans un domaine de fréquences comprises entre 400 et 750 terahertz (THz) environ, ce qui équivaut à des longueurs d’onde entre 400 et 800 nm environ. Les échelles de taille présentées ici sont détaillées sur cette page.

En réalité, parler de la fréquence d’une onde lumineuse ou d’énergie ne fait aucune différence. Un gymnaste s’exerçant sur des barres asymétriques donne alors une image de cette interaction entre la lumière et la matière. Lorsque le gymnaste fournit suffisamment d’énergie, il peut passer de la barre du bas à la barre du haut. De la même façon, lorsqu’un atome absorbe un rayonnement — une onde lumineuse — il gagne de l’énergie et se trouve dans l’état du haut qui est dit excité. Lorsque le gymnaste repasse au niveau du bas, il n’a plus la même amplitude dans ses mouvements et, en général, il s’économise un peu… De même, l’atome peut émettre un rayonnement, perdre de l’énergie et se désexciter. De cela, il faut retenir que les changements d’énergie ne peuvent se produire que par sauts, comme ces transitions d’une barre à l’autre.

Deux niveaux d’énergie différents

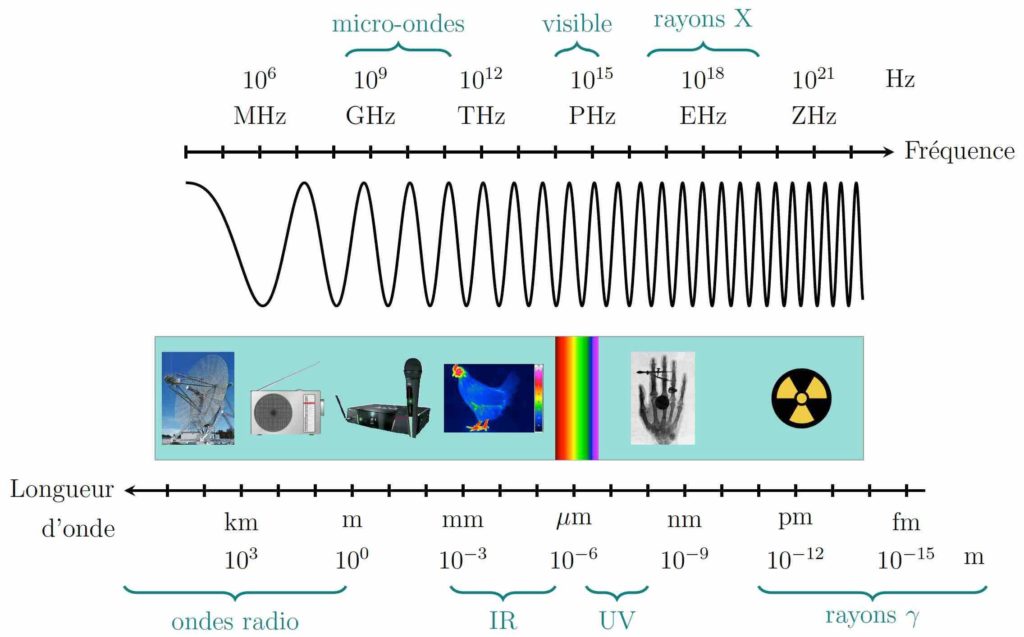
Pour revenir à la « version atomique » du gymnaste, on peut se représenter l’atome comme un noyau avec des électrons qui gravitent autour. Ces électrons ne peuvent se trouver qu’à des distances particulières du noyau, un peu comme différents paliers. Un changement d’énergie correspond à un changement brutal d’orbite — de palier — pour un électron. Ce processus définit une première échelle d’énergie pour les états atomiques : les fréquences de transition, qui sont dans le domaine de la lumière visible (voir Figure 2).

Toutefois, pour la transition des atomes de césium permettant de définir l’unité de temps, l’excitation de l’atome correspond à une situation différente, en lien avec ses propriétés magnétiques. À la manière de deux aimants, l’électron le plus externe et le noyau interagissent et donnent ainsi naissance à deux niveaux d’énergie selon que leurs aimantations sont alignées ou bien anti-alignées. L’énergie de la transition mise en jeu pour l’alignement ou l’anti-alignement correspond alors à une deuxième échelle bien plus petite que dans le cas du changement d’orbite d’un électron. En effet, la transition s’effectue sous l’effet d’un rayonnement aux alentours de 9,2 gigahertz (GHz), soit une fréquence bien plus faible que celles du rayonnement visible (entre 400 et 750 terahertz (THz)). C’est plus de 100 000 fois plus petit ! (voir Figure 2). On parle de rayonnement micro-onde et de transition radiofréquence (noté RF). Pour le gymnaste, les barres sont dans ce cas disposées bien plus proches l’une de l’autre, si bien qu’une moindre énergie est nécessaire pour passer de l’une à l’autre. L’horloge à césium, constituant l’étalon primaire — mesure qui sert de référence à toutes les autres mesures — dans la mesure du temps, exploite précisément cette transition RF entre les deux barres asymétriques des niveaux d’énergie magnétiques de l’atome de césium.

L’horloge à césium

Le principe de fonctionnement général d’une horloge est résumé sur la Figure 3 à gauche et ses principales caractéristiques à la Figure 3 à droite. L’intérêt de la transition atomique RF — dans le cas du césium — est de fournir, lorsque l’environnement des atomes n’est pas perturbé, une référence immuable de fréquence à 9 192 631 770 hertz. Autrement dit, lorsque l’on excite les atomes de césium, ils répondent toujours de la même façon, ce qui permet d’avoir une mesure du temps absolument toujours identique. Cette excitation se fait grâce à un four à micro-ondes bien particulier : une cavité RF, c’est-à-dire une enceinte métallique abritant le rayonnement RF fourni par un oscillateur local. On dit que la cavité RF réalise « l’interrogation » des atomes.

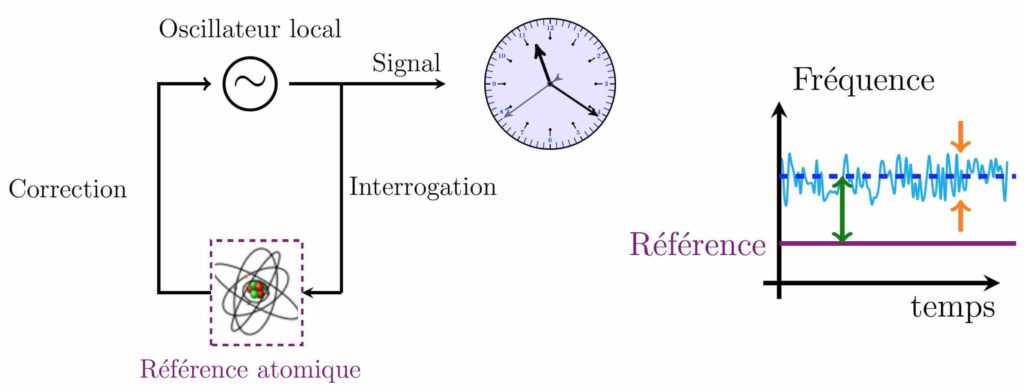
À gauche, on a une flèche qui lie "interrogation" à "référence atomique" puis une autre flèche qui va jusque "correction" puis "oscillateur local". De l'oscillateur va ensuite vers "signal" et une horloge. À droite, graphique de la fréquence en fonction du temps. On a une ligne violette annotée "référence" et au-dessus, une courbe bleue avec plein de petits pics. Flèche verte entre la courbe bleue et la ligne violette. Double-flèche qui encadre la courbe bleue. — **Figure 3. À gauche**, schéma de principe d’une horloge se basant sur une référence de césium. À chaque instant, un oscillateur électrique envoie un signal à une fréquence d’environ 9,2 GHz pour « interroger » des atomes de césium et provoquer la transition alignement/anti-alignement évoquée dans le texte. En se désexcitant, l’atome renvoie sa fréquence immuable de référence. On corrige ensuite le décalage entre le signal de l’oscillateur électronique et la référence. Enfin, un compteur transforme ce signal bâti sur la référence pour l’unité de temps en heure réelle. **À droite**, la flèche verte, qui symbolise l’écart de fréquence du signal d’horloge par rapport à la référence, représente l’inexactitude de l’horloge, c’est-à-dire l’écart statique entre la valeur d’interrogation et la valeur de référence. L’amplitude des fluctuations, représentée par les flèches oranges, se réfère à son instabilité.

L’oscillateur local est un dispositif électronique permettant de fournir un signal de fréquence donnée assez proche de la fréquence associée à la transition des atomes (environ 9,2 GHz) et relativement stable. En interrogeant les atomes avec ce dernier, la transition entre les deux niveaux d’énergie de l’atome de césium, correspondant à un électron externe et un noyau d’aimantations alignées/anti-alignées, génère un rayonnement à la fréquence exacte de référence. Il suffit alors de corriger, avec une boucle électronique, l’erreur entre l’interrogation par l’oscillateur local et la réponse des atomes pour obtenir un signal d’horloge performant, où la fréquence de l’oscillateur local sera précisément accordée avec l’énergie de la transition des atomes de césium : l’horloge sera toujours à l’heure.

Deux critères principaux permettent de juger du caractère performant du signal d’horloge ainsi généré :

l’imprécision par rapport à la référence, qui est l’écart en fréquence indiqué en vert sur la Figure 3 à droite. Cet écart provient de l’erreur systématique commise entre l’interrogation et la correction, par exemple à cause des effets de l’environnement sur les atomes (température extérieure, etc.).
l’instabilité, représentée sur la Figure 3 à droite par l’amplitude des fluctuations indiquée en orange. Ces écarts aléatoires d’une boucle interrogation/correction à une autre, par rapport à la valeur moyenne de toutes les boucles, peuvent se produire lorsque, entre deux instants successifs, l’interrogation des atomes change d’un iota (pour une raison quelconque).

Au fil des années, précision et stabilité des étalons primaires à base de césium ont connu des améliorations fulgurantes grâce à des techniques d’interrogation de plus en plus savantes, comme par exemple l’utilisation de fontaines de césium [1]. Ces horloges au césium particulières, dans lesquelles les atomes sont en chute libre, parviennent à une stabilité relative en fréquence record : de l’ordre de $2\times 10^{-16}$ au bout d’une seconde d’interrogation des atomes. Une comparaison possible de cette remarquable stabilité consiste à estimer le nombre d’années nécessaires pour observer une dérive d’une seconde complète : environ une centaine de millions d’années (c’est le temps qui nous sépare de la période géologique du crétacé, à la fin de laquelle les dinosaures ont disparu). Tandis que seules deux minutes de dérive nous séparent du Big Bang (soit 13,7 milliards d’années) !

**Figure 4.** Photographie d’une horloge atomique ultra-performante mais peu compacte, fonctionnant sur la base d’une fontaine de césium. Cette horloge est également développée au NIST. Crédit : NIST, domaine public.

L’horloge atomique développée par S. Knappe et ses collègues est une horloge au césium, mais, pour eux, hors de question de produire une référence de temps occupant un volume comparable à celui de l’horloge de la Figure 4 ! Il s’agit plutôt d’avoir la performance des horloges atomiques dans le format d’une montre. Les pouvoirs de Superman dans le corps d’une sauterelle !

Quelles astuces pour faire tenir les atomes dans la poche ?

Les horloges à fontaine de césium ont certes une stabilité remarquable mais elles possèdent un inconvénient rédhibitoire quand il s’agit de réduire leur taille : leur cavité RF. En effet, sa taille doit être au minimum de l’ordre de 3 cm, et à cela vient s’ajouter l’appareillage nécessaire à la phase de préparation des atomes : système de refroidissement des atomes, mise en forme du jet de la fontaine, etc. Tout cela devient vite encombrant ! Or, il faut savoir que les performances de l’horloge dépendent directement du temps d’interrogation des atomes par la cavité RF. Pour que le temps d’interaction soit élevé, il faut donc que la cavité soit large. Hélas, il est très difficile de fabriquer des cavités RF beaucoup plus longues que 3 cm [2]. Une autre amélioration, très répandue, est en fait encore plus encombrante : elle consiste à réaliser une interrogation par non plus une mais plusieurs cavités RF espacées ! Après ce constat autour de la phase d’interrogation des atomes, il paraît bien difficile de réduire le volume des horloges à base de césium…

Première astuce : une interrogation optique

Une première astuce utilisée par S. Knappe et ses collègues consiste à simplement s’affranchir des cavités RF en exploitant à la place un autre type d’interrogation des atomes de césium. Ils excitent pour cela les atomes de manière optique, grâce à l’envoi simultané de deux faisceaux laser rouges quasiment identiques. Quasiment, car ils présentent une très légère différence de fréquence entre eux : précisément égale à 9,2 GHz. Et c’est justement cette différence de fréquence entre les deux lasers qui permet, par des effets quantiques, l’excitation de l’atome de césium à précisément 9,2 GHz. C’est comme si le gymnaste évoqué précédemment, pas très doué pour les sauts de puce, décidait de passer de la barre du bas à une barre située 10 cm plus haut en faisant un premier saut de 1,1 m vers une troisième barre bien plus haute avant de redescendre dans un second saut 1 m plus bas [*]. Cette méthode d’excitation des atomes de césium permet de conjuguer un fort potentiel métrologique (= une très grande précision de la fréquence) et un encombrement minime, puisqu’il n’est plus nécessaire d’utiliser une cavité RF encombrante.

Deuxième astuce : un laser à semiconducteurs

La deuxième astuce consiste à utiliser un type particulier de laser à semiconducteurs comme source pour l’interrogation optique des atomes. Ce type de lasers s’adapte facilement à la longueur d’onde visée, produit des faisceaux de bonne qualité et connaît un essor industriel remarquable, si bien que les téléphones portables de la prochaine génération en embarqueront trois pour la reconnaissance faciale et la 3D [3]. Ils sont faciles à produire à grande échelle car s’obtiennent à partir de grandes plaques à semiconducteurs savamment déposées que l’on sépare ensuite en micro-puces… un peu comme un gâteau dans lequel on se servirait de minuscules parts ! Les deux rayons rouges légèrement décalés en fréquence qui servent à l’interrogation entièrement optique des atomes sont issus d’un seul et même laser à semiconducteurs, ce qui permet là encore de limiter l’encombrement.

Troisième astuce : un système électromécanique miniaturisé

**Figure 5**. Photographie de l’horloge atomique miniature développée par Knappe et son équipe au NIST. Crédit : NIST, domaine public.

Il en résulte une micro-structure de volume final 9,5 mm³ (soit un cube d’environ 3 mm de côté, comme la gomme de votre critérium préféré) et consommant seulement 75 mW (c’est 50 000 fois plus qu’une banale montre à quartz, mais 5 000 fois moins qu’un ordinateur de bureau). Une grande partie de cette puissance n’est utile qu’à chauffer la cellule de césium à 85 °C pour augmenter la densité d’atomes. Une pile fera l’affaire !

Ces horloges miniatures sont-elles performantes ?

À ce point là, la stratégie disruptive de S. Knappe et ses collègues a porté ses fruits : ils ont construit la première horloge atomique de poche compatible avec une production industrielle. Mais est-elle suffisamment performante pour remplacer une bonne vieille montre à quartz ?

Leur horloge obtient une stabilité relative en fréquence de $2{,}4\times 10^{-10}$ pour 1 seconde d’interrogation, avec un minimum d’environ $2{,}5\times 10^{-11}$ pour 250 secondes d’interrogation. Certes, ces performances sont loin des records obtenus avec les fontaines à césium ( $2\times 10^{-16}$ pour 1 seconde d’interrogation, voir plus haut) mais comparons-les plutôt aux montres à quartz pour plus d’équité (à volume plus ou moins équivalent). Un diapason à quartz de montre-bracelet atteint typiquement une instabilité relative en fréquence de $10^{-7}$ sur un jour, soit quelques secondes de dérive par an (c’est déjà pas mal pour être à l’heure !) [4]. Ici, on est plutôt sur $10^{-10}$ , c’est donc 1 000 fois plus stable ! L’intérêt d’une référence atomique prend alors tout son sens.

Lorsque, pour des communications militaires par exemple, il n’est pas possible d’utiliser un signal satellite type GPS (le satellite embarque lui-même une horloge à fontaine de césium), le diapason en quartz d’une bonne montre ne suffira pas à fournir une référence assez stable, contrairement aux horloges atomiques miniatures développées par S. Knappe et son équipe. Une entreprise américaine a d’ailleurs profité de cette innovation pour équiper à large échelle l’armée des États-Unis de ces horloges atomiques de la taille d’une puce électronique.

Non seulement les horloges atomiques miniatures présentent des performances intéressantes, mais leurs limites sont aussi bien identifiées, ce qui offre des perspectives prometteuses d’amélioration en agissant sur :

l’environnement des atomes de césium dans la cellule. Les isoler des perturbations extérieures participe à la stabilité de l’horloge ;
le niveau de bruit du laser (c’est-à-dire ses fluctuations), qui contribue à l’instabilité de l’horloge à travers l’interrogation des atomes ;
l’intensité lumineuse du laser. L’augmenter est avantageux pour réduire le bruit relatif du laser. Mais il ne faut pas non plus faire saturer le photodétecteur en sortie de la cellule de césium, ce qui pourrait détériorer des performances de l’horloge. On note, en partie pour cette raison, l’utilisation de verres teintés atténuateurs dans le dispositif optique de la puce ;
la stabilité de la température. Les fluctuations thermiques participent significativement au bruit des lasers à semiconducteurs. Plus la température est stable dans la puce, plus l’horloge sera stable.

En bref, les horloges miniatures à base de césium amènent avec leur développement une percée technologique qui ne vise pas un record de stabilité mais un compromis entre volume et stabilité complètement inédit.

[*] Les deux lasers rouges ont une fréquence d’environ 852 nm. En fait, si on garde les proportions entre la transition optique à 852 nm (c’est-à-dire 352 THz) et la transition RF à 9,2 GHz, la seconde barre n’est pas située à 10 cm mais plutôt à quelques centièmes de millimètres.

[1] Billy N., Fabre C., « Panorama de la physique — Horloges et métrologie ». Belin : pour la science, 2012, ISBN : 9782701165004. [Livre de science]

[2] Cohen-Tannoudji C., Horloges atomiques et atomes ultra-froids. Congrès du centenaire de l’UDPPC, Besançon, 2006. [Résumé de conférence]

[3] 3D sensing in smartphones is pushing the VCSEL industry, Electronicspecifier.com, 28 Juillet 2018. [Article de presse, en anglais]

[4] Marc J., et al., Le diapason à quartz comme capteur : utilisation de la carte son de PC pour l’instrumentation. Bulletin de l’Union des Physiciens, vol. 107, 2013. [Ressource scientifique et pédagogique]

Publié le 14/10/2020

Grégory Gredat/Papier-Mâché/CC BY-NC-SA 4.0 2020

Texte et images, à l’exception des images soumises à droits d’auteurs différents : voir au cas par cas en légende.

Écriture : Grégory Gredat
Relecture scientifique : Léo Mangeolle
Relecture de forme : Jérémy Ferrand

Temps de lecture : environ 16 minutes.
Thématiques : Photonique (Physique)

Publication originale : Knappe S., et al., A microfabricated atomic clock. Applied Physics Letters, 2004. DOI : 10.1063/1.1787942

Une brève histoire du temps et de sa mesure

Depuis la 13^e conférence générale des poids et mesures en 1967, la définition de l’unité du système international pour la mesure du temps, la seconde, repose sur la transition entre deux niveaux d’énergie dits hyperfins du césium 133 (¹³³Cs) à l’état fondamental. En effet, la fréquence de cette transition est fixée à exactement f = 9 192 631 770 Hz. S’il est équivalent de parler de différence d’énergie et de fréquence d’un rayonnement, c’est que l’absorption ou bien l’émission d’un rayonnement par les atomes accompagne l’excitation ou bien la désexcitation de ces derniers. La relation de Planck-Einstein établit alors la proportionnalité entre la différence d’énergie $E_2-E_1$ entre les deux niveaux hyperfins en question et la fréquence f de l’onde électromagnétique correspondant à la transition des atomes de césium d’un niveau d’énergie à l’autre. Mais qu’est-ce qu’un niveau d’énergie hyperfin ?

L’électron externe de l’atome de césium dans son état fondamental possède un moment magnétique, dû à son spin (une de ses propriétés quantiques). Le noyau ¹³³Cs, qui est le seul isotope stable du césium, possède également un moment magnétique avec lequel celui de l’électron interagit, à la façon de deux aimants. Le niveau d’énergie de l’électron externe se scinde alors en deux niveaux dits hyperfins d’énergies légèrement différentes selon que le moment magnétique de l’électron est aligné ou anti-aligné avec celui du noyau. On notera $\left|1\right>$ et $\left|2\right>$ les états électroniques associés à ces niveaux d’énergie. Cette interaction magnétique est très faible, ce qui implique que la différence $E_{2} - E_{1}$ est minime par rapport aux énergies atomiques usuelles. Ramené en fréquences, avec l’équivalence évoquée plus haut, cela revient à comparer un rayonnement micro-onde à 10 GHz aux fréquences du rayonnement visible qui se situent entre 400 et 750 THz. Voilà pourquoi la structure des sous-niveaux d’énergie est qualifiée d’hyperfine. La transition associée est, de plus, très étroite : on calcule, pour cette transition, un facteur de qualité $Q = f/\Delta f$ , avec $\Delta f$ la largeur naturelle [*] de l’ordre de 10⁷. L’horloge à césium, constituant l’étalon primaire dans la mesure du temps, exploite précisément cette transition hyperfine dont la finesse donne tout l’intérêt métrologique.

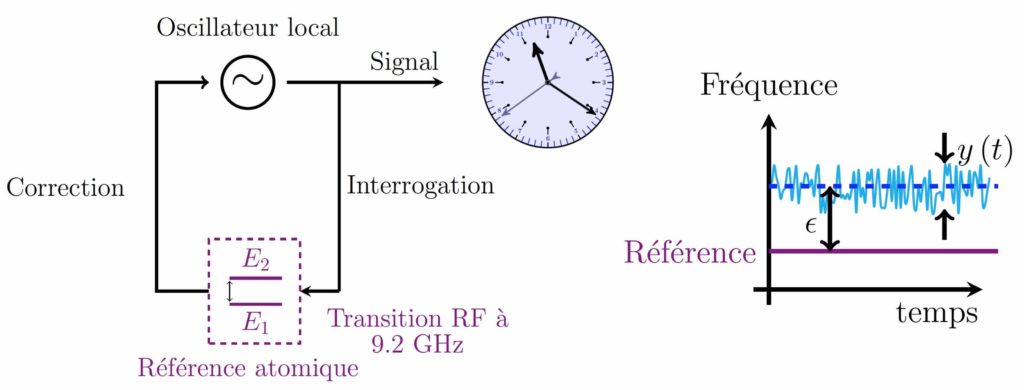
À gauche, on a une flèche qui lie "interrogation" à un picto indiquant "référence atomique" ainsi que "transition RF à 9,2 GHz" et deux traits E2 et E1. Ensuite, une autre flèche qui va jusque "correction" puis "oscillateur local". De l'oscillateur va ensuite vers "signal" et une horloge. À droite, graphique de la fréquence en fonction du temps. On a une ligne violette annotée "référence" et au-dessus, une courbe bleue avec plein de petits pics. Flèche avec la lettre epsilon entre la courbe bleue et la ligne violette. Double-flèche avec y(t) qui encadre la courbe bleue. — **Figure 1.** **À gauche**, schéma de principe d’une horloge se basant sur une référence de césium. **À droite**, inexactitude ε et instabilité y(t) de la fréquence du signal d’horloge. Transition RF : transition radiofréquence.

Le principe de fonctionnement général d’une horloge est résumé sur la Figure 1 à gauche et ses principales caractéristiques à droite. L’intérêt de la transition atomique — radiofréquence (RF) dans le cas du césium — est de fournir, lorsque l’environnement des atomes n’est pas perturbé, une référence immuable de fréquence sur laquelle on vient asservir [**] un oscillateur local. Autrement dit, lorsque l’on excite la transition hyperfine des atomes de césium grâce à une cavité RF (enceinte métallique abritant le champ électromagnétique RF fourni par un oscillateur local), les atomes répondent toujours de la même façon. On dit que la cavité RF réalise « l’interrogation » des atomes. Il suffit alors de corriger, avec une boucle électronique, le signal d’erreur entre l’interrogation par l’oscillateur local et la réponse des atomes pour obtenir un signal d’horloge performant. Comme l’indique la Figure 1 à droite, deux critères principaux permettent de juger du caractère performant du signal d’horloge ainsi généré :

l’imprécision, qui est l’écart relatif $\epsilon$ en fréquence par rapport à la fréquence de la transition ;
l’instabilité, qui représente l’amplitude relative 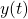$y(t)$ des fluctuations de fréquence, toujours par rapport à la fréquence de référence.

Au fil des années, précision et stabilité des étalons primaires à base de césium ont connu des améliorations fulgurantes grâce à des techniques d’interrogation de plus en plus savantes, comme par exemple l’utilisation de fontaines de césium [1]. Ces horloges au césium, dans lesquelles les atomes sont en chute libre, parviennent à une stabilité relative en fréquence record de l’ordre de $2\times 10^{-16}$ , pour une interrogation des atomes de 1 seconde. Une comparaison marquante de cette remarquable stabilité consiste à estimer le nombre d’années nécessaires pour observer une dérive d’une seconde complète, qui se situe vers la centaine de millions d’années (c’est le temps qui nous sépare de la période géologique du crétacé, à la fin de laquelle les dinosaures ont disparu). Tandis que seules deux minutes de dérive nous séparent du Big Bang (soit 13,7 milliards d’années) !

**Figure 2.** Photographie d’une horloge atomique ultra-performante mais peu compacte, à base d’atomes froids de strontium, développée au laboratoire JILA du Colorado. Crédit : NIST, domaine public.

À cause de la transition à 9,2 GHz entre les niveaux hyperfins, les horloges au césium font partie de la famille des horloges dites micro-ondes (avec celles au rubidium et à l’hydrogène). Les horloges optiques (calcium, ytterbium, strontium, mercure, aluminium, etc.) constituent une autre grande famille d’horloges atomiques. Le développement des horloges optiques a connu un essor récent considérable, si bien qu’elles servent aujourd’hui d’étalons secondaires pour la seconde. Par exemple, l’horloge optique basée sur des atomes froids de strontium piégés dans un treillis optique de la Figure 2 atteint une précision remarquable de $2{,}5\times 10^{-19}$ seconde d’écart par seconde [2], c’est-à-dire qu’il faut plus d’un milliard de milliard de secondes au signal d’horloge pour que l’écart à sa référence atomique soit d’une seconde. En comparaison, pour un système de navigation par satellites comme le GPS, l’erreur relative commise si l’on ne tient pas compte des effets relativistes est de l’ordre de $10^{-10}$ s par seconde, soit un milliard de fois plus important que l’imprécision de l’horloge optique. Sur le plancher des vaches, cette erreur correspondrait à un écart de positionnement de 10 km par jour si l’on omet la théorie de la relativité restreinte contre à peine 10 µm pour l’imprécision de l’horloge optique.

L’horloge atomique développée par S. Knappe et ses collègues est une horloge micro-onde au césium, mais, pour eux, hors de question de produire une référence de temps occupant un volume comparable à celui de l’horloge de la Figure 2. Il s’agit plutôt d’avoir la performance des horloges atomiques dans le format d’une montre (Figure 3). Les pouvoirs de Superman dans le corps d’une sauterelle !

**Figure 3**. Photographie de l’horloge atomique miniature développée par Knappe et son équipe au NIST. Crédit : NIST, domaine public.

Quelles astuces pour faire tenir les atomes dans la poche ?

Les horloges à jets de césium ont certes une stabilité remarquable mais elles possèdent un inconvénient rédhibitoire quand il s’agit de réduire leur taille : leur cavité micro-onde résonante. En effet, la longueur d’onde associée à la transition RF de $f = 9{,}2$ GHz vaut $c/f = 3$ cm, où $c$ est la célérité de la lumière dans le vide. La taille de la cavité micro-onde doit être de l’ordre de cette longueur d’onde, et à cela vient s’ajouter l’appareillage nécessaire à la phase de préparation des atomes (système de refroidissement des atomes, mise en forme du jet, etc., tout cela devient vite encombrant). L’évolution temporelle de la probabilité de transition des atomes, mesurée en sortie de cellule, est une courbe en cloche (une résonance) de largeur typique 1 $\tau$ , où $\tau$ représente le temps d’interaction des atomes dans la cavité RF [3]. Il faut bien comprendre que les performances de l’horloge dépendent directement de la qualité de la résonance, dont la largeur est d’autant plus faible que le temps d’interaction est élevé, donc la cavité large. Or, avec une cavité de taille caractéristique $l = 3$ cm et un jet d’atomes dont la vitesse atteint $v = 300$ m/s, le temps d’interaction est seulement de $\tau = 100$ µs. Une amélioration consisterait à augmenter la largeur de la cavité résonante ; hélas, il est très difficile de fabriquer des cavités RF résonantes à des longueurs d’ondes beaucoup plus longues que 3 cm. Une autre amélioration, très répandue, est en fait encore plus encombrante. Elle consiste à réaliser une interrogation, dite de Ramsey, par non plus une mais plusieurs cavités RF espacées. Dans ce cas, la largeur de la résonance n’est désormais que par le temps d’évolution libre entre deux cavités RF. Pour obtenir une horloge performante, on a donc intérêt à augmenter la distance qui sépare les cavités RF mais cela va à l’encontre de la réduction de la taille du dispositif. Après ce constat autour de la phase d’interrogation des atomes, il paraît bien difficile de réduire le volume des horloges à base de césium.

Une première astuce utilisée par S. Knappe et ses collègues consiste à simplement s’affranchir des cavités RF en exploitant à la place un effet quantique propre à une interrogation entièrement optique des atomes. Elle suppose d’utiliser un troisième niveau d’énergie, noté $\left|3\right>$ sur la Figure 4 à gauche, qui peut être atteint par excitation des atomes de césium grâce à un rayonnement rouge à 852 nm. En variant la fréquence de l’onde en incidence d’une cellule contenant des vapeurs de césium, on note sans surprise une large bande d’absorption représentée en tirets gris sur la Figure 4 à droite.

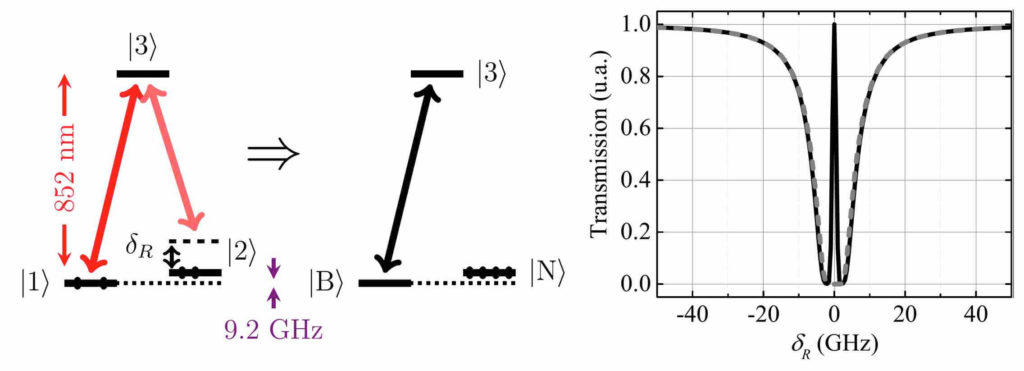
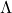À gauche, un trait qui monte puis un trait qui descend. Au milieu, le même trait qui monte, mais seul. À droite, une courbe qui décroît jusque presque GHz, puis fait un bic très fort et brutal puis la courbe recroît de manière symétrique. — **Figure 4. À gauche**, système en $\Lambda$ à partir du diagramme d’énergie du césium. 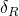$\delta_R$ : désaccord à deux photons. **Au milieu**, système équivalent à résonance et piégeage dans l’état noir 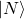$\left|N\right>$ . À droite, intensité transmise par la cellule en fonction du désaccord 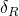$\delta_R$ . On observe le pic spectral typique de la transparence induite par le piégeage cohérent de population (courbe noire) par inhibition de l’absorption (tirets gris) due au pompage optique [***] dans l’état noir.

En envoyant simultanément deux faisceaux laser rouges aux alentours de 852 nm présentant une légère différence de fréquence, on construit alors le système en $\Lambda$ (d’après la forme de la lettre grecque) représenté à la Figure 4, à gauche.

Cependant, lorsqu’il y a précisément une différence de 9,2 GHz entre les deux ondes lumineuses, on a une résonance étonnante à deux photons et la fréquence du désaccord $\delta_R$ [****], défini sur la figure, est nulle. À la résonance, une superposition quantique entre les états $\left|1\right>$ et $\left|2\right>$ , appelée état noir (noté $\left|N\right>$ ), correspond à un niveau d’énergie du système qui a la particularité d’être immunisé du couplage dipolaire électrique. En d’autres termes, lorsque les atomes se trouvent dans cet état, ils deviennent en quelque sorte transparents au champ électromagnétique. Par contre, les deux autres états propres s’expriment comme des superpositions d’états faisant intervenir l’état excité $\left|3\right>$ , dont la durée de vie est très faible (de l’ordre de la ns) comparé aux autres.

Quelques cycles d’absorption puis émission suffisent alors pour pomper optiquement la population dans l’état noir $\left|N\right>$ , comme l’illustre la Figure 4, au milieu. L’état $\left|B\right>$ montré sur cette figure est l’état brillant qui est, à l’inverse, défini comme une autre superposition des états fondamentaux qui se couple au champ de lumière (d’où son nom). Une fois dans l’état noir, les atomes se retrouvent piégés dans ce même état pendant un temps bien long devant la désexcitation du niveau $\left|3\right>$ , c’est pourquoi le phénomène est désigné par CPT en anglais pour coherent population trapping. La résonance à deux photons provoque ainsi un pic de transparence lorsque l’on scanne le désaccord en fréquence $\delta_R$ (Figure 4 à droite), c’est-à-dire lorsque l’on varie finement la longueur d’onde d’un des faisceaux laser. La largeur de ce pic de résonance CPT est fondamentalement limitée par l’inverse d’un temps caractéristique $T$ de l’ordre de quelques millisecondes, dû à des phénomènes quantiques complexes. La grande finesse du pic de transparence, qui possède un facteur de qualité potentiel $Q = 2\pi fT$ , se situant entre $10^7$ et $10^8$ , permet de conjuguer un fort potentiel métrologique et un encombrement minime, puisqu’il n’est plus nécessaire d’utiliser une cavité RF.

La deuxième astuce de S. Knappe et son équipe pour minimiser la taille est d’utiliser une diode laser à semiconducteurs comme source pour l’interrogation des atomes. Ces lasers à cavité verticale émettant par la surface (VCSEL pour l’acronyme anglais) s’adaptent facilement à la longueur d’onde visée, produisent des faisceaux de bonne qualité et connaissent un essor industriel remarquable, si bien que les téléphones portables de la prochaine génération en embarqueront trois pour la reconnaissance faciale et la 3D [4]. Ils sont faciles à produire à grande échelle car s’obtiennent à partir de grandes plaques à semiconducteurs savamment déposées que l’on sépare ensuite en micro-puces, un peu comme un gâteau dans lequel on se servirait de minuscules parts ! À l’aide d’une modulation à $f_m = 4{,}6$ GHz du courant de pompe de ce laser, le pic d’émission, situé vers 852 nm (352 THz), se sépare en deux pics distants de $2f_m = 9{,}2$ GHz. Changer la fréquence de modulation permet de scanner le pic de transmission de la cellule de césium en déplaçant l’une de l’autre les deux composantes du VCSEL. À résonance, quand leur séparation est de 9,2 GHz, on obtient un maximum de transparence à cause du CPT et donc un maximum d’intensité lumineuse transmise. À l’aide d’un photodétecteur en sortie de cellule, la mesure d’une légère baisse de signal est contrebalancée par une rétroaction sur la fréquence de modulation qui permet ainsi un asservissement de l’oscillateur local sur la résonance atomique : c’est la phase de correction que nous avons mentionnée à la Figure 1 à gauche. On construit ainsi le système en $\Lambda$ précédent avec un seul laser, ce qui permet là encore de limiter l’encombrement.

En plus de cette interrogation optique des atomes, l’astuce ultime ayant mené au développement complet des horloges atomiques miniatures, c’est l’intégration des éléments précédents à un microsystème électromécanique. L’obtention de l’horloge de la taille d’une puce (Chip scale atomic clock en anglais) nécessite des procédés innovants de micro-fabrication, adaptés à la production en masse, que l’article de S. Knappe décrit en détails. La micro-puce électro-optique est constituée d’un empilement de matériaux qui forment successivement (de bas en haut sur la Figure 3) le VCSEL, un dispositif optique (principalement une micro-lentille, des filtres teintés et une lame quart-d’onde), la cellule de césium puis la photodiode. Il en résulte une micro-structure de volume final 9,5 mm $^{3}$ et consommant seulement 75 mW. Une grande partie de cette puissance n’est utile qu’à chauffer la cellule de césium à 85 °C pour augmenter la densité atomique dans la vapeur. Une pile fera l’affaire !

Ces horloges miniatures sont-elles performantes ?

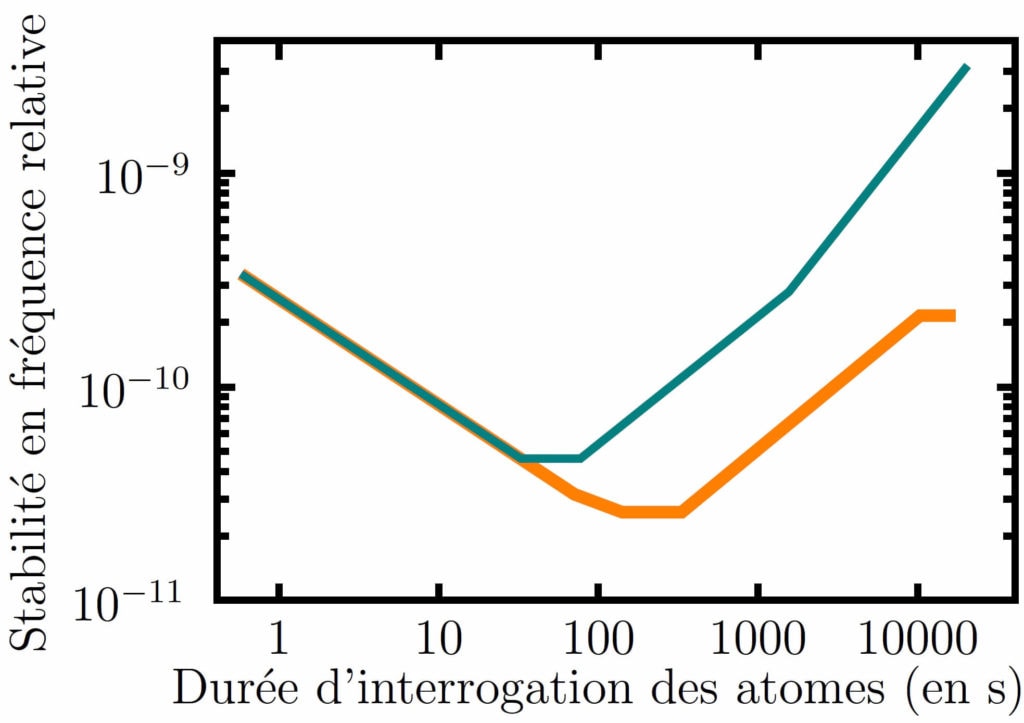
La Figure 5 affiche le résultat de leur mesure de la stabilité relative en fréquence de l’horloge. On lit une valeur de $2{,}4 \times 10^{-10}$ pour 1 seconde d’interrogation, pour l’instabilité relative qui atteint un minimum d’environ $5 \times 10^{-11}$ pour une minute et demi d’interrogation (courbe turquoise). Les auteurs identifient toutefois une dérive systématique de $-2 \times 10^{-8}$ par jour causée par la modification de la pression du gaz tampon à l’intérieur de la cellule, nécessaire pour limiter les effets dus aux collisions des atomes sur les parois. Étant en capacité de corriger cette erreur systématique, ils retranchent cette contribution à leurs mesures (courbe orange) et obtiennent un nouveau minimum d’instabilité de $2{,}5 \times 10^{-11}$ pour 250 secondes d’interrogation. Certes, ces performances sont loin des records présentés en première partie ( $2 \times 10^{-16}$ pour 1 seconde d’interrogation) mais comparons-les plutôt aux montres à quartz pour plus d’équité (à volume plus ou moins équivalent). Un diapason à quartz commercial de montre atteint typiquement une instabilité relative en fréquence de 10 $^{-7}$ sur un jour, soit quelques secondes de dérive par an (c’est déjà pas mal pour être à l’heure !) [5]. Ici, on est plutôt sur $10^{-10}$ d’après la Figure 5, soit trois ordres de grandeurs plus stables ! L’intérêt d’une référence atomique prend alors tout son sens.

Deux courbes turquoise et orange en forme de "v". Au début les 2 sont superposées et décroissent puis la turquoise croît avant la orange et monte plus haut. — **Figure 5. Stabilité en fréquence relative de l’horloge miniature en fonction de la durée d’interrogation des atomes de césium.** La courbe issue des données brute est en turquoise alors que pour la courbe orange, les auteurs ont retranché une dérive linéaire de la fréquence d’horloge.

Lorsque, pour des communications militaires par exemple, il n’est pas possible d’utiliser un signal satellite type GPS (le satellite embarque lui-même une horloge à jet de césium), le diapason en quartz d’une bonne montre ne suffira pas à fournir une référence assez stable, contrairement aux horloges atomiques miniatures développées par S. Knappe et son équipe. Une entreprise américaine a d’ailleurs profité de cette innovation pour équiper à large échelle l’armée des États-Unis de ces horloges atomiques de la taille d’une puce électronique.

Notons tout de même qu’il ne faut pas mettre trop rapidement sa montre au placard. Les meilleures références à base de diapasons en quartz stabilisés peuvent atteindre les 10 $^{-13}$ sur une longue durée d’interrogation et la recherche demeure active à ce sujet. Mais soit le volume total occupé par ces oscillateurs exceptionnels n’est pas encore comparable à l’horloge miniature que nous décrivons, soit leur industrialisation est nettement plus compliquée.

Non seulement les horloges CPT miniatures présentent des performances intéressantes, mais leurs limites sont aussi bien identifiées, ce qui offre des perspectives prometteuses d’amélioration en agissant sur :

l’environnement des atomes de césium dans la cellule. Les isoler participe à la stabilité de l’horloge. Un blindage magnétique par exemple peut être utilisé pour éviter un décalage parasite des niveaux d’énergie, proportionnel au champ magnétique ressenti par un atome (effet Zeeman) ;
le niveau de bruit du laser (c’est-à-dire ses fluctuations). En effet, les bruits d’amplitude et de phase du laser contribuent à l’instabilité de l’horloge à travers l’interrogation des atomes. Un pompage du VCSEL à une puissance élevée minimise ses fluctuations. Il faut, d’autre part, s’assurer que la modulation à 4,6 GHz ne propage pas une source supplémentaire de bruit, d’origine électronique par exemple ;
l’intensité lumineuse du laser. L’augmenter est avantageux pour le bruit relatif d’intensité du VCSEL, comme nous venons de l’évoquer. C’est également le cas pour le bruit relatif lié à la limite de détection de la photodiode placée après la cellule de césium. Cependant, il ne faut pas non plus faire saturer la photodiode. En outre, un vrai compromis se doit d’être trouvé puisque la largeur de la résonance CPT, elle, s’élargit proportionnellement à l’illumination reçue. On note, probablement pour ces raisons, l’utilisation de verres teintés atténuateurs dans le dispositif optique de la puce ;
la stabilité de la température. Le chauffage de la structure du VCSEL à 46 °C permet d’accorder son émission à la bonne longueur d’onde (852 nm), mais imposer un écart thermique par rapport à la température ambiante présente certains inconvénients. C’est, d’une part, synonyme d’une certaine consommation électrique, et d’autre part, d’un bruit accru du VCSEL. En effet, les fluctuations thermiques participent significativement au bruit des lasers à semiconducteurs puisque l’indice optique du milieu à gain varie beaucoup avec la température. Plus la température est stable dans la puce et plus l’horloge sera stable, ce qui mène usuellement à l’utilisation d’une stabilisation thermique active à l’aide de modules à effet Peltier [*****]. Un léger changement de la structure à semiconducteurs du laser est envisageable pour une émission à 852 nm à température ambiante.

En bref, les horloges CPT miniatures amènent avec leur développement une percée technologique qui ne vise pas un record de stabilité mais un compromis entre volume et stabilité complètement inédit.

Pour les records de stabilité, c’est du côté des horloges optiques qu’il faut se tourner. Ces horloges sont si performantes qu’elles ont rendu possible sur Terre la mesure d’effets gravitationnels de dilatation du temps prédits par la théorie de la relativité générale [6]. Imaginons une première référence de temps ultra-stable placée au pied du Tokyo Skytree (ou, pourquoi pas, du mont Fuji) et une seconde référence placée au sommet, les deux étant initialement synchronisées. Le champ gravitationnel terrestre ressenti par la première horloge est plus intense que celui ressenti par l’horloge en hauteur, en conséquence de quoi la théorie de la relativité générale prédit son retard par rapport à la seconde horloge. Plus précisément, pour chaque centimètre d’élévation de la seconde horloge, l’horloge restée au sol retarde d’un ordre de grandeur de 10 $^{-18}$ s quand en hauteur il s’écoule 1 seconde. Ce chiffre (un milliardième de milliardième de seconde) permet de réaliser le défi technologique conséquent, concernant la stabilité et la précision de l’horloge développée, relevé là aussi pour mener de telles mesures (sur une durée totale d’à peine une demi-année).

Le développement des références de temps, et plus généralement des étalons pour la métrologie, répond ainsi à de très larges enjeux modernes en sciences physiques s’étalant de la science fondamentale jusqu’à l’utilisation pratique de ces systèmes (géolocalisation, etc.). L’article de S. Knappe apporte une contribution importante pour l’embarquabilité de ces dispositifs.

[*] La durée de vie finie (mais longue) du niveau hyperfin $\Delta t$ impose un minimum d’incertitude $\Delta E$ sur l’énergie de la transition résultant de l’inégalité d’Heisenberg sur le produit $\Delta E \cdot \Delta t$ . On appelle largeur naturelle $\Delta f$ , le minimum d’incertitude en fréquence proportionnel à cette incertitude sur l’énergie.

[**] Un asservissement est un système, généralement électronique, visant à atteindre le plus rapidement possible une valeur de consigne et à la maintenir, indépendamment des perturbations externes. Son fonctionnement repose d’abord sur la comparaison de cette consigne à l’état du système puis sur la correction de l’écart éventuellement constaté. Par exemple, un système d’air conditionné est un asservissement : en fonction de la température mesurée, le dispositif chauffe ou refroidit l’air pour maintenir la pièce à la température souhaitée.

[***] Pompage optique : réalisation d’une inversion de population sous l’action d’une onde lumineuse puissante. L’inversion de population est une situation dans laquelle un niveau d’énergie se trouve plus peuplé qu’un autre état d’énergie plus basse. Cette situation n’est pas la plus courante puisque dans un système laissé à l’équilibre, ce sont les états les plus bas en énergie qui sont statistiquement plus peuplés (voir État fondamental) ; elle ne peut se produire qu’hors de l’équilibre thermodynamique. On montre qu’un minimum de trois niveaux d’énergie est nécessaire pour obtenir l’inversion de population. Dans ce cas, le phénomène d’émission induite peut devenir plus important que celui de l’absorption, une propriété à la base du fonctionnement des lasers. On doit le concept de pompage optique et sa mise en œuvre pour la première fois en 1950 à Alfred Kastler.

[****] Ce désaccord à deux photons est appelé désaccord Raman, d’après le nom du lauréat indien du prix Nobel de 1930.

[*****] Effet Peltier : effet thermique accompagnant un déplacement de charges (courant électrique) se produisant entre deux matériaux conducteurs différents reliés par deux jonctions. Une différence de température entre les deux jonctions apparaît alors.

[1] Billy N., Fabre C., « Panorama de la physique — Horloges et métrologie ». Belin : pour la science, 2012, ISBN : 9782701165004. [Livre de science]

[2] Marti G. E., et al., Imaging Optical Frequencies with 100 µHz Precision and 1.1 µHz Resolution. Phys. Rev. Lett., 2018. DOI : 10.1103/PhysRevLett.120.103201. [Publication scientifique]

[3] Cohen-Tannoudji C., Horloges atomiques et atomes ultra-froids, Congrès du centenaire de l’UDPPC, Besançon, 2006. [Résumé de conférence]

[4] 3D sensing in smartphones is pushing the VCSEL industry, Electronicspecifier.com, 28 Juillet 2018. [Article de presse, en anglais]

[5] Marc J., et al., Le diapason à quartz comme capteur : utilisation de la carte son de PC pour l’instrumentation. Bulletin de l’Union des Physiciens, vol. 107, 2013. [Ressource scientifique et pédagogique]

[6] Takamoto M., et al., Test of general relativity by a pair of transportable optical lattice clocks. Nature Photonics, 2020. DOI : 10.1038/s41566-020-0619-8. [Publication scientifique]

Publié le 14/10/2020

Grégory Gredat/Papier-Mâché/CC BY-NC-SA 4.0 2020

Texte et images, à l’exception des images soumises à droits d’auteurs différents : voir au cas par cas en légende.

La publication scientifique facile à digérer !