Écriture : Ronan Delalande
Relecture scientifique :  Jérémy Ferrand
Relecture de forme : Viet Chau Linh Nguyen et Eléonore Pérès

Temps de lecture : environ 15 minutes.
Thématiques : Mécanique des matériaux (Physique)

Publication originale : Hitchman S., et al., Monitoring attenuation and the elastic properties of an apple with laser ultrasound. Postharvest Biology and Technology, 2016. DOI : 10.1016/j.postharvbio.2016.07.006

C’est l’indécision devant l’étal de fruits et légumes. Lequel prendre ? Est-il est mûr ? Il a de belles couleurs mais reste ferme. Et celui-là ? Il semble plus mou, est-ce qu’il tiendra quelques jours avant de pourrir ? … Tant de questions ! Et si on tirait dessus avec un laser pour savoir si ce fruit est mûr ?

Le menu de la semaine est bien établi. La liste de courses est bien rédigée. Au programme, entre autres, une tarte aux pommes. Mais une fois devant les fruits et légumes, voilà le complexe de l’étal ! Quelles pommes prendre ? Est-ce que celles-ci sont assez mûres ? Si, finalement, la tarte n’est que pour la semaine prochaine, est-ce qu’il ne vaudrait pas mieux prendre des fruits un peu verts et leur laisser le temps de finir de mûrir ? On juge à l’aspect visuel d’abord : la forme, la couleur… Et puis finalement, avant de prendre la décision finale, on prend en main le fruit qui a attiré notre œil pour tester sa fermeté.

Tâter une pomme, ou à ce titre n’importe quel fruit, pour connaître sa maturité, la stratégie est bien connue et pratiquée quotidiennement devant les étalages de fruits et légumes. Toute molle ? Cette pomme est sans doute pourrie ! Très dure ? Pas assez mûre ! Au travers de ce geste anodin c’est, au final, un essai mécanique qui est réalisé. De nos doigts, ce n’est pas directement la maturité que l’on teste mais bien les propriétés mécaniques du fruit. Notre cerveau fait le travail grâce à nos expériences passées d’associer la rigidité et la dureté de la pomme à sa maturité attendue.

Rien qu’en France, 1,5 millions de tonnes de pommes sont produites annuellement [1]. À 150 g en moyenne la pomme [2], cela représente au final 10 milliards de fruits ! Voilà de quoi s’occuper un petit moment pour déterminer lesquelles sont mûres ! Pourtant, outre-Manche, au Royaume-Uni en 2007, on estimait à 190 000 tonnes la quantité de pommes jetées chaque année [3]. Contrôler la qualité et la maturité des fruits pourrait être important pour réduire ces pertes de fruits, et donc d’énergie, de temps et d’argent.

Tout le long des chaînes de production, contrôler la qualité des fruits, notamment au travers de leur maturité, est un défi du quotidien. Pas question d’amener des fruits sur l’étal qui soient plus durs que du bois. À l’inverse, des pommes dont l’avenir se limiterait à un composteur ne trouveraient pas grand intérêt aux yeux des clients. Cette question de la bonne tenue des fruits ne date pas d’hier. L’un des principaux indices utilisés pour suivre la maturité des fruits est l’indice de fermeté de Magness-Taylor (MT), des noms des chercheurs ayant publié leur étude il y a 100 ans [4]. Seul souci, la technique éponyme associée à cet indice est destructive, puisqu’elle consiste à presser de plus en plus fort le fruit jusqu’à ce qu’il éclate. Donc, plus vraiment de pomme à la sortie de l’opération. D’autres techniques ont été proposées, s’intéressant à l’absorption de certaines lumières par le fruit [5] ou à la façon dont il résonne [6]. De cette dernière approche a notamment été introduit un nouvel indice de fermeté nommé très sobrement Indice de Fermeté, largement utilisé aujourd’hui et directement proportionnel à l’indice MT [7]. Même si ces techniques de vibrations ou de lumière ne demandent plus de détruire le fruit, elles restent relativement chronophages et peu adaptées à une utilisation plus systématique pour de grandes quantités de fruits.

Le défi est donc de trouver une méthode pour tester efficacement et rapidement la maturité d’un fruit sans l’abîmer. Voilà la question à laquelle s’est intéressée une équipe de recherche néo-zélandaise ! La solution proposée repose sur deux aspects : des lasers et du son !

Des ondes indic du milieu

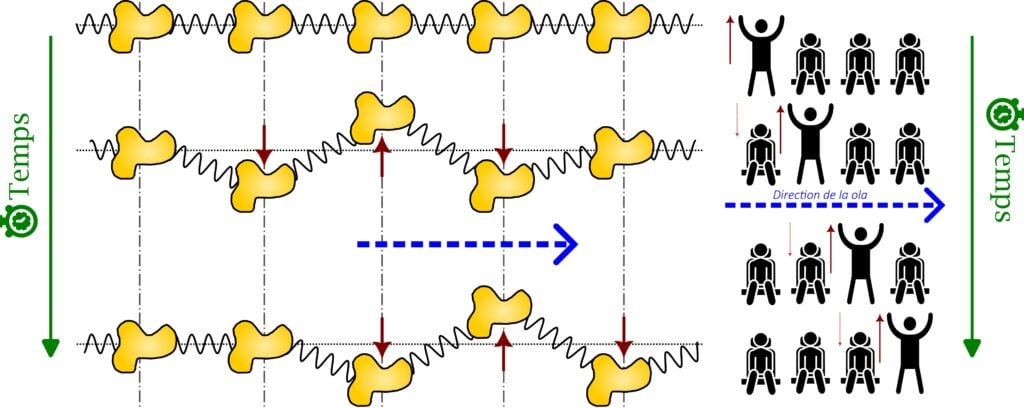
Tout d’abord, il faut comprendre ce qu’est une onde. On a déjà tous et toutes entendu ce terme, mais que signifie-t-il ? On peut faire un exercice de visualisation. Vous êtes dans un stade, prêt à assister à une rencontre sportive de votre équipe préférée. Les gradins sont pleins. Chacun est assis sur son siège, à attendre que les athlètes entrent en piste. Personne ne bouge, le public est au repos. Puis, soudainement, une ola. Une petite partie des gens sont debout pendant que tout le reste de l’audience est encore au repos. Il y a une perturbation du public qui se propage dans la foule. Une fois la ola passée, vous êtes de nouveau assis, au repos. Même après des tours et des tours de stades de ola, vous êtes encore sur votre propre siège. Personne ne s’est déplacé, il n’y a pas eu de transport, c’est-à-dire de déplacement, de personnes. Avec cette ola, une ferveur se transmet de proche en proche, de spectateur en spectateur (Figure 1).

Une onde c’est ça ! Une perturbation d’un milieu se transmettant de proche en proche sans transport de matière mais avec un transfert d’énergie. Et des ondes, il y en a partout et de différentes sortes. On distingue notamment deux grandes familles : les ondes électromagnétiques et les ondes mécaniques. La lumière est un exemple d’ondes électromagnétiques, qui ont l’avantage de pouvoir se propager même sans support matériel. La Terre et le Soleil sont séparés par un peu moins de 150 millions de km de vide, et pourtant la lumière nous parvient quand même. Les vagues à la surface de l’eau sont quant à elles des ondes mécaniques, tout comme le son. À la différence de la lumière, ces ondes ont besoin d’un support. Il peut s’agir de n’importe quel milieu matériel comme de l’air, de l’eau, de l’acier, etc. ou le cœur d’une pomme, mais pas de vide ! C’est la raison pour laquelle, dans l’espace, personne ne vous entend crier [*].

Si les ondes sont omniprésentes, leurs caractéristiques peuvent grandement varier. En particulier, la vitesse de propagation est un paramètre essentiel. Dans le vide, la lumière (une onde lumineuse donc) se propage à 299 792 458 mètres par seconde (m/s) et met plus de 8 minutes à faire la distance Terre-Soleil. Les ondes mécaniques sont beaucoup plus lentes et leurs vitesses dépendent fortement du milieu. Si on reprend l’exemple de la ola, une étude réalisée à partir d’extraits vidéos de la coupe du monde de football de Mexico de 1986 avait donné la valeur de 12 m/s [8]. Dans l’air, les sons que nous émettons et entendons se propagent à une vitesse de l’ordre de 340 m/s. Dans l’eau, ces mêmes sons se propageant avec une vitesse un peu inférieure à 1 500 m/s tandis que dans des milieux solides ils iraient encore bien plus vite. On retient souvent la vitesse de 6 400 m/s dans l’aluminium ou jusqu’à 12 000 m/s dans certains matériaux céramiques.

Là où les choses se compliquent un peu plus c’est qu’il peut exister dans les milieux solides différents types d’ondes, qui se distinguent par le mouvement que suivent les particules. On parle de polarisation : comment est-ce que les particules se déplacent par rapport au déplacement de l’onde ? Reprenons le cas de la ola, schématisée sur la Figure 2 : l’onde se propage de la gauche vers la droite (flèche pointillée bleue), pourtant les spectateurs se déplacent eux de haut en bas (flèches rouges). Le mouvement des « particules constituant le milieu » (c’est-à-dire des spectateurs constituant le public) est perpendiculaire à la direction de propagation de l’onde. On parle d’une onde transverse. 

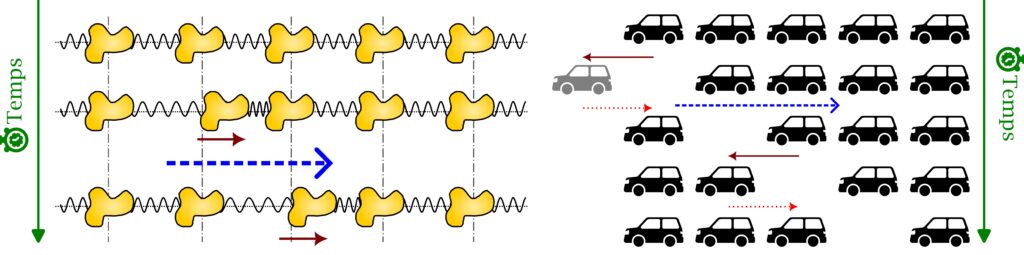
Prenons un autre exemple de la vie quotidienne, les bouchons, schématisé sur la Figure 3 vus par un piéton sur le trottoir. La perturbation ─ l’espacement entre les voitures ─ va de gauche à droite. Mais cette fois-ci « les particules », les voitures, vont-elles aussi de droite à gauche. Les mouvements des particules et celui de l’onde vont selon la même direction : on parle d’une onde longitudinale. Ces deux types d’ondes (transversale et longitudinale) peuvent coexister dans un même milieu mais ne se propagent pas à la même vitesse. Si on prend un métal bien connu comme l’aluminium, on a vu plus haut que l’onde longitudinale se propage à 6 400 m/s. Par contre, l’onde transverse est plus lente avec une vitesse de seulement 3 000 m/s.

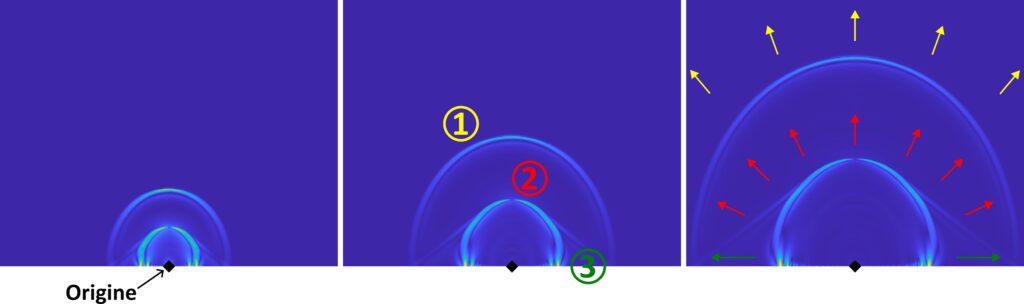
Si ces deux ondes peuvent se propager indépendamment dans un milieu, il est également possible qu’elles se combinent. C’est notamment le cas lorsque le milieu n’est pas infini et qu’il existe des frontières. Par exemple, les bords des gradins constituent des frontières du public lorsque l’on regarde une ola. Parmi les ondes plus compliquées obtenues par combinaison, on peut citer les ondes de Rayleigh qui sont des ondes de surface. Elles se propagent uniquement le long d’une frontière. Dans la pomme, de telles ondes font ainsi le tour du fruit en suivant la peau mais sans jamais la quitter (ni vers le centre du fruit, ni en sortant du fruit). À cause de cette interaction avec le bord (ici, la peau de la pomme), les ondes de Rayleigh sont légèrement plus lentes encore que les ondes transverses. La Figure 4 présente une image issue d’une simulation : une coupe d’un milieu matériel dans lequel les trois ondes (longitudinale, transverse, de Rayleigh) sont générées. Les deux premières, respectivement en flèches jaunes pleines et rouges pointillées, se propagent dans toutes les directions et forment des arcs de cercles. L’arc de cercle de l’onde longitudinale est plus grand car cette onde est plus rapide. L’onde de Rayleigh (flèches vertes en tirets) se contente juste de suivre le bord.

Cependant, toutes ces ondes ne se propagent pas jusqu’au bout de l’univers sans s’arrêter. Au fur et à mesure de leur voyage, elles perdent de l’énergie, entre autres sous forme de chaleur : les ondes s’atténuent. Cette perte progressive de l’énergie peut également être une caractéristique permettant de discriminer différents milieux ou matériaux. L’atténuation est ainsi beaucoup plus importante dans du verre que dans un métal. Et cette différence peut se sentir avec les mains : si vous lâchez une bille de verre et une bille en aluminium par terre de la même hauteur (pas de trop haut bien sûr), la bille en aluminium vibrera et fera du bruit plus longtemps.

Si la vitesse des ondes diffère d’un milieu à l’autre, ce n’est pas simplement par hasard mais à cause des propriétés mécaniques de ces milieux. Si l’on connaît les propriétés mécaniques d’un milieu, il est possible de déterminer les vitesses des ondes longitudinales, transverses ou de Rayleigh. Mais, l’inverse est également possible : si l’on connaît les vitesses des différentes ondes, on peut déduire les propriétés mécaniques du milieu. Les relations entre vitesses et propriétés sont plus ou moins complexes selon la nature du milieu. Mais une pomme est un milieu simple : elle est homogène et isotrope, c’est-à-dire que toutes les propriétés mécaniques sont les mêmes quel que soit le point dans la pomme que l’on considère. Pour un milieu comme celui-ci, il suffit de deux paramètres pour le caractériser mécaniquement : le module de Young et le coefficient de Poisson. Je vous explique ça tout de suite.

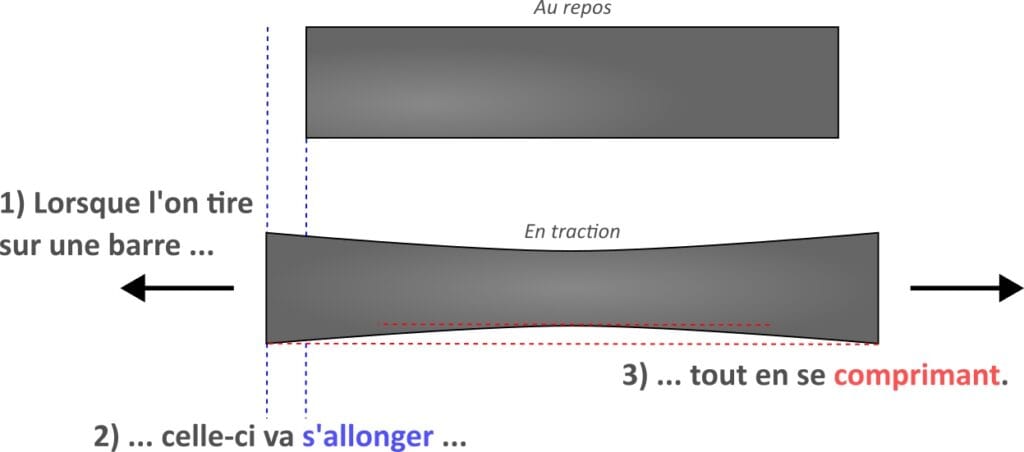
Prenons une barre, comme dessinée sur la Figure 5. Lorsque l’on tire ses deux extrémités, deux phénomènes peuvent être observés : la barre s’allonge mais va aussi s’amincir. Le module de Young caractérise l’allongement. Plus il est important, plus il faut tirer fort pour allonger la barre d’une certaine longueur, c’est-à-dire plus la matière que compose la barre est rigide. Le coefficient de Poisson caractérise quant à lui l’amincissement : plus le coefficient de Poisson est grand, plus la barre va s’amincir pour une force donnée. Des matériaux différents vont présenter des propriétés différentes. L’acier et l’aluminium par exemple présentent des coefficients de Poisson presque égaux, mais le module de Young est 3,5 fois plus important pour l’acier. Si on tire avec la même force sur une barre d’acier et une barre d’aluminium, cette dernière sera plus longue. Mais le rapport entre l’allongement et l’amincissement sera le même pour les deux barres. Cette différence a pour conséquences des vitesses des ondes également différentes entre les deux milieux.

Au cours de leur étude, l’équipe néo-zélandaise a proposé de mesurer l’atténuation mais aussi les vitesses de propagation des trois ondes (longitudinale, transverse et de Rayleigh) citées. À partir de ces dernières, il est possible de calculer le module de Young ainsi que le coefficient de Poisson de la pomme.

Des lasers pour faire du son

Si l’idée d’utiliser des ondes semble simple sur le papier, encore faut-il pouvoir le faire. Il faut d’abord les générer. Une première approche pourrait être, par exemple, de directement taper sur une pomme avec un marteau. Mais cette idée semble surtout être la meilleure manière d’abîmer la pomme. Sans compter le temps nécessaire pour taper une à une chacune des pommes, il faudrait s’assurer que l’on tape toujours de la même façon pour pouvoir véritablement comparer deux essais. La méthode proposée par l’équipe de recherche est bien différente : tirer sur la pomme avec des lasers !

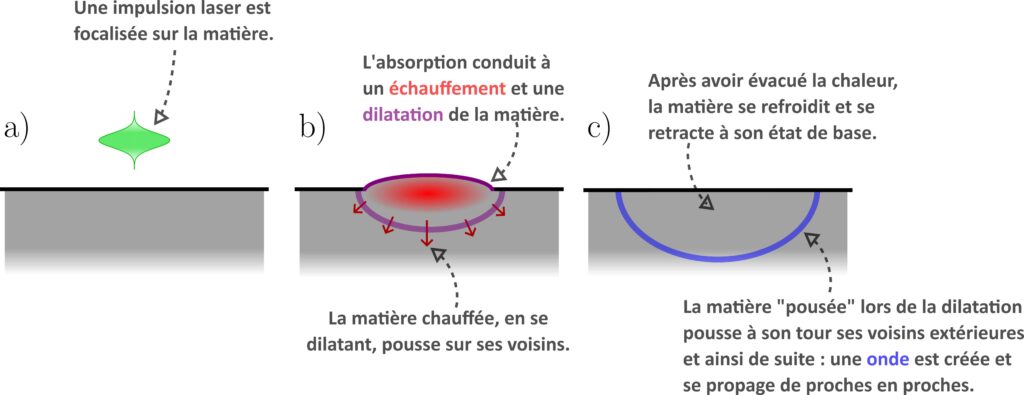
Lorsque de la lumière arrive sur un objet, une partie est réfléchie mais une autre portion peut également être absorbée par la matière. L’énergie lumineuse est convertie, entre autres, en énergie thermique. La température de l’objet augmente, comme schématisé sur la Figure 6. En général, cette augmentation de température est faible car la quantité de lumière est également assez faible. Sauf si l’on se met à utiliser des lasers ! Ce type de source développée à partir des années 1960 [9] permet de concentrer une quantité importante d’énergie optique sur une petite surface. Cette concentration conduit donc à un échauffement non négligeable de la matière. Si la source lumineuse diminue, voire est éteinte, l’apport d’énergie cesse. La matière chauffée se refroidit et se recontracte, revenant à son état initial. Sauf qu’entre-temps, en se chauffant, la matière éclairée s’est dilatée et a exercé une pression sur son entourage. Cette pression est une perturbation qui se propage de proche en proche. Une onde mécanique vient d’être générée à l’aide de l’impulsion laser. Mis en évidence à la fin du XIX^e siècle [10], ce procédé de génération d’onde à l’aide de sources laser impulsionnelles s’utilise aujourd’hui de plus en plus. Il permet en effet de générer les ondes sans mettre le moindre appareil en contact avec l’échantillon étudié.

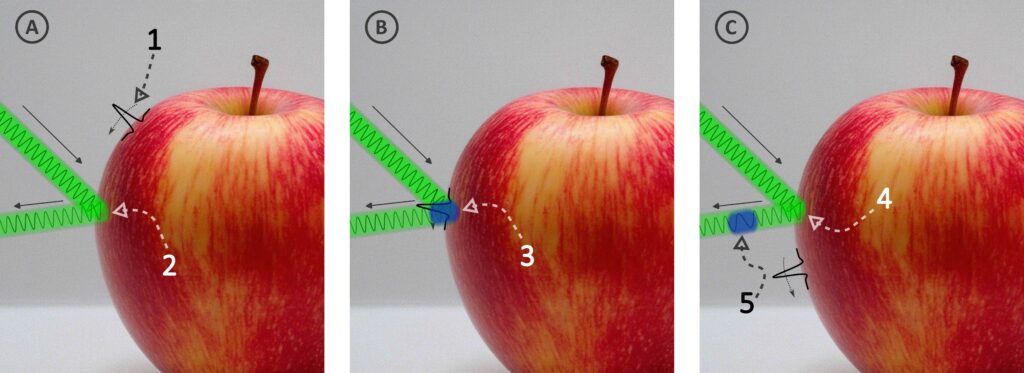
Une fois les ondes générées, il reste encore à les détecter pour pouvoir en déduire une quelconque vitesse. Là aussi, un laser est l’instrument de choix. Comme dit précédemment, une partie de la lumière est réfléchie lorsqu’elle arrive sur un objet. La lumière réfléchie, en l’occurrence le faisceau laser, contient de l’information sur l’objet qu’elle a rencontré et notamment sur ses vibrations. Si la pomme est au repos, qu’elle ne bouge pas ni ne vibre pas, alors la réflexion de la lumière est toujours la même. Par contre, si la pomme se déforme, même très légèrement comme c’est le cas au passage d’ondes, alors le faisceau réfléchi est modifié. La lumière rencontre un objet en mouvement, un effet particulier se produit : l’effet Doppler. Cet effet, on le connaît bien lorsqu’une ambulance avec gyrophare se rapproche de nous, passe à grande vitesse devant nous puis s’éloigne aussi vite. La tonalité perçue semble changer, allant d’un son aigu vers un son plus grave, même si le bruit émis par l’ambulance est bien toujours le même. La fréquence du son change en raison du déplacement de l’origine de ce son. Pour ce qui nous intéresse ici, cet effet Doppler se produit également lorsqu’un son est émis et rencontre un objet en déplacement. Si l’effet Doppler existe pour les ondes mécaniques comme le son, on le retrouve également pour les ondes électromagnétiques telle que la lumière. La fréquence d’un faisceau laser rencontrant un objet en mouvement est affectée par ce mouvement, comme schématisé sur la Figure 7. Le passage d’une onde n’entraîne qu’un mouvement très petit de la matière, de l’ordre de 0,000 000 000 1 m [11], comparable à la taille d’un atome. Le faisceau réfléchi à la surface de la pomme n’est que très peu modifié. Mais en le combinant avec un faisceau de référence, qui n’a pas vu la pomme, il est possible de révéler la modification due au mouvement.

Un son lent ? un fruit prêt à la dégustation !

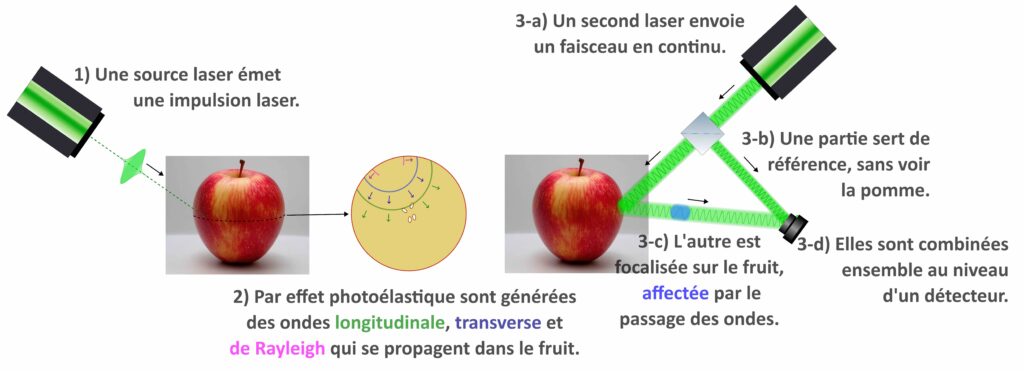
Un laser tire sur une pomme pour générer des ondes mécaniques dans celle-ci. Un second laser sert à détecter quand les ondes arrivent de l’autre côté de la pomme. Pendant 15 jours, tous les jours, voilà la mesure réalisée sur la même pomme par l’équipe néo-zélandaise avec un montage similaire à celui dessiné sur la Figure 8.

Et chaque jour, les temps que mettent les ondes à traverser ou à faire le tour de la pomme augmentent un peu. Les ondes sont de plus en plus lentes. De ces observations, l’équipe de recherche trouve par exemple que l’onde longitudinale, se propageant initialement à environ 182 m/s, perd 1,5 m/s par jour. Et le signal mesuré est de plus en plus faible. Pourtant, la génération est toujours la même ! C’est donc que les ondes s’atténuent de plus en plus dans la pomme au fil des jours. Même tendance pour l’onde de Rayleigh.

Les mesures indiquent des variations, soit, encore faut-il savoir si ces variations ont un sens, si elles peuvent servir à déterminer la maturité de la pomme. Mais aussi, est-ce que tous les paramètres sont vraiment nécessaires : les trois vitesses, les trois atténuations, les deux modules ? Est-ce qu’un seul indicateur ne suffirait-il pas ? Pour répondre à ces questions, les scientifiques ont réalisé des mesures de vibrations de la pomme pour calculer le fameux FI, indice de rigidité, afin qu’il serve de référence. Après 15 jours d’expériences, l’équipe de recherche a montré que l’atténuation de l’onde de Rayleigh diminuait deux fois plus vite que l’indice FI. Ce critère, plus sensible, semble donc être parfait pour suivre finement l’évolution d’une pomme !

Finalement, l’équipe néo-zélandaise a démontré que des lasers pouvaient être utilisés pour générer mais aussi détecter des ondes mécaniques dans une pomme. En réalisant ces essais, elle a surtout mis en avant que le comportement de ces ondes change dans le temps. Ces variations s’expliquent par des modifications des propriétés mécaniques de la chair du fruit, au fur et à mesure qu’il mûrit. La technique proposée est à la fois non-destructive car elle n’abîme pas la pomme et rapide puisque seules quelques millisecondes sont nécessaires pour faire une mesure. Restent à régler les questions des coûts mais surtout de la sécurité avant de voir tous les entrepôts de fruits et légumes s’équiper de lasers. Si cette méthode permet de suivre l’évolution voire d’évaluer l’état de maturité, quelques questions sont encore en suspens avant de l’utiliser dans l’industrie agroalimentaire : à partir de quel module de Young ou d’atténuation des ondes de Rayleigh est-ce qu’on considère qu’une pomme est pourrie ? La réponse viendra peut-être de collaborations entre scientifiques et cheffes et chefs cuisiniers, qui cherchent par exemple à fabriquer la tarte tatin parfaite en prenant notamment en compte les propriétés mécaniques des pommes [12].

---

[*] Accroche promotionnelle du film Alien.

---

[1] Synthèse conjoncturelles Fruits – Pommes, agreste, Mai 2024 (pdf). [Rapport]

[2] Quel est le poids moyen d’une pomme ? Info et astuce, Double Portion, 2021 – dernière consultation le 13/11/2024. [Site web]

[3] Weekly food waste collections can benefit the environment and save money, DEFRA, 2008 – dernière consultation le 13/11/2024 [Site web]

[4] Magness J. R. & Taylor G. F., An improved type of pressure tester for the determination of fruit maturity, U.S. Dept. of Agriculture, 1925. [Publication scientifique]

[5] Peng Y., et al., Prediction of apple fruit firmness and soluble solids content using characteristics of multispectral scattering images. J. Food Eng., 2007. DOI : 10.1016/j.jfoodeng.2006.12.027. [Publication scientifique]

[6] Abbott J.A., et al., Sonic techniques for measuring texture of fruits and vegetables, Food Technol., 1968. [Publication scientifique]

[7] Duprat F., et al., The acoustic impulse response method for measuring the overall firmness of fruit. J. Agric. Eng. Res., 1997. DOI : 10.1006/jaer.1996.014. [Publication scientifique]

[8] Farkas, I., et al., Mexican waves in an excitable medium. Nature, 2002. DOI : 10.1038/419131a. [Publication scientifique]

[9] Maiman, T. H., Stimulated optical radiation in ruby, Nature, 1960. DOI : 10.1038/187493a0. [Publication scientifique]

[10] Bell A. G., On the production and reproduction of sound by light, American journal of science, 1880. DOI : 10.2475/ajs.s3-20.118.305. [Publication scientifique]

[11] Scruby S. C. & Drain L. E., Laser Ultrasonics Techniques and Applications, 1990. DOI : 10.1201/9780203749098. [Livre de science]

[12] García-Segovia P., et al.. Improvement of a culinary recipe by applying sensory analysis: Design of the New Tarte Tatin. International Journal of Gastronomy and Food Science, 2012. DOI: 10.1016/j.ijgfs.2011.11.011. [Publication scientifique]

---