Chargement de l'article...
Écriture : Léo Mangeolle
Relecture scientifique : Dorian Vigoureux et Éric Brillaux
Relecture de forme : Aurélien Didier et Garance Meyer
Temps de lecture : environ 13 minutes.
Thématiques : Matière condensée (Physique)
Publication originale : Berezinskii V. L., Destruction of Long-range Order in One-dimensional and Two-dimensional Systems having a Continuous Symmetry Group I. Classical Systems. Journal of Experimental and Theoretical Physics, 1971.

Pourquoi, à basse température, l’eau se change-t-elle en glace ? La réponse à cette question repose sur les concepts d’ordre et de symétrie. Pour décider de l’état dans lequel se trouvera la matière, un match se joue en effet entre la symétrie et l’ordre, en fonction des conditions dans lesquelles le système se trouve, et en particulier de la température ambiante. Dans son article de 1971, V. Berezinskii explore le rôle d’un autre paramètre important, la dimension, en se focalisant sur celle où la physique est la plus étonnante : la dimension 2.
L’enjeu de la rencontre
Quelle est la différence entre l’eau et la glace ? D’un point de vue macroscopique, c’est assez facile : il s’agit de deux états de l’espèce chimique H2O, l’état liquide (l’eau s’écoule) et l’état solide (la glace reste figée). D’accord ; mais si l’on zoome jusqu’à l’échelle des molécules, comment fait-on la différence entre une goutte d’eau et un glaçon, puisque ce sont les mêmes molécules qui les constituent ? Plus généralement, l’une des tâches de la physique consiste à faire la distinction, à l’échelle microscopique, entre les différentes phases de la matière. Le terme générique de phase regroupe notamment :
- les différents états d’un corps pur (liquide, gaz, cristal, etc.), qui correspondent à l’agencement des atomes ou des molécules dans l’espace ;
- les différentes structures magnétiques qui correspondent à l’organisation d’un grand nombre « d’aimants élémentaires », les spins, dans un matériau. Par exemple, la phase ferromagnétique, caractéristique d’un matériau aimanté, ou la phase paramagnétique, sans aimantation propre ;
- bien d’autres exemples de phases, pouvant correspondre au comportement isolant ou conducteur d’un solide, à la répartition spatiale des différents ingrédients dans une vinaigrette, ou encore aux mouvements d’un banc de poissons.
Il est possible de classer beaucoup de ces phases en deux catégories [1] (Figure 1) :
- d’une part, les phases ordonnées, comme par exemple la phase cristalline (où les atomes sont régulièrement disposés dans l’espace, par exemple la glace) ou encore la phase ferromagnétique (où les spins sont tous alignés dans une seule direction, résultant en une phase globalement aimantée, et donc en un aimant) ;
- d’autre part, les phases désordonnées, comme par exemple la phase liquide (où les atomes sont éparpillés aléatoirement dans l’espace, par exemple l’eau) ou encore la phase paramagnétique (où l’orientation des spins fluctue dans toutes les directions, ce qui explique que la phase n’ait pas d’aimantation globale propre).
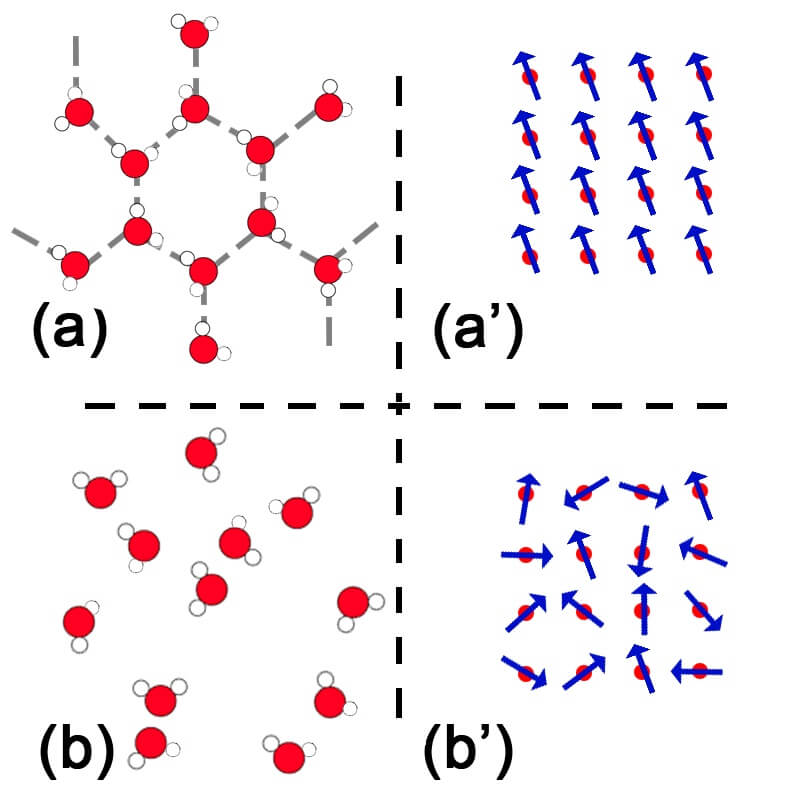
Si cette première classification permet de distinguer l’eau de la glace à l’échelle microscopique, est-elle toutefois suffisante pour décrire toutes les phases existant dans la nature ?
Dans son article, V. Berezinskii s’intéresse à un cas assez particulier qui sort de ce cadre : les systèmes à deux dimensions. On peut penser, par exemple, à un film d’hélium liquide (comme un film de savon, mais constitué d’hélium) (Figure 2). Le cas de la dimension 2 est particulier car :
- d’une part, les films d’hélium liquide présentent des caractéristiques expérimentales propres à ce fluide, qui sont à la fois absentes dans les fines couches d’eau, d’huile, de savon, etc., mais également absentes de l’hélium liquide en 3D. Une de ces caractéristiques, par exemple, est la façon dont les films d’hélium liquide interagissent avec le récipient ;
- d’autre part, une description théorique de l’hélium 2D est difficile à obtenir. Si l’on dispose de nombreux outils statistiques pour décrire les systèmes 3D [2] et de certains outils mathématiques pour les systèmes 1D, les systèmes bidimensionnels constituent un cas intermédiaire généralement très ardu.

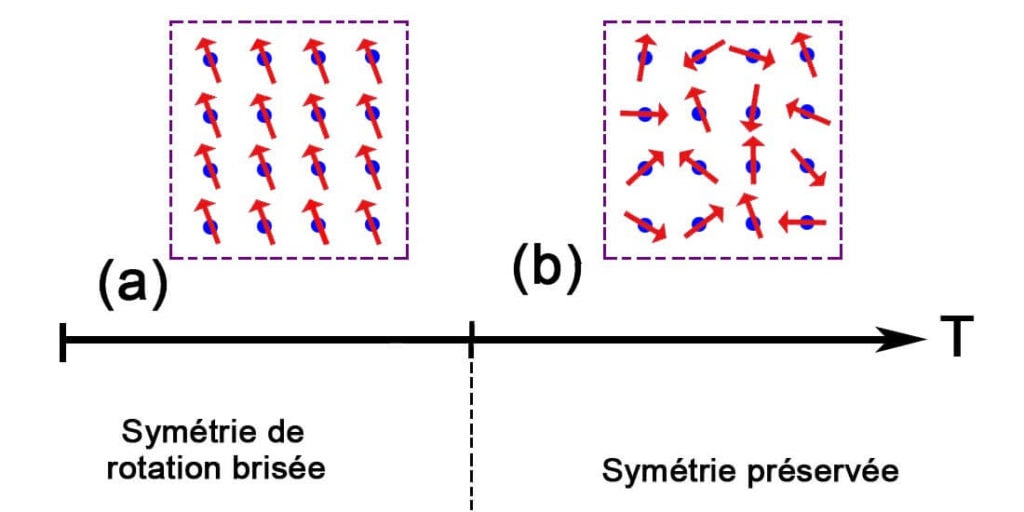
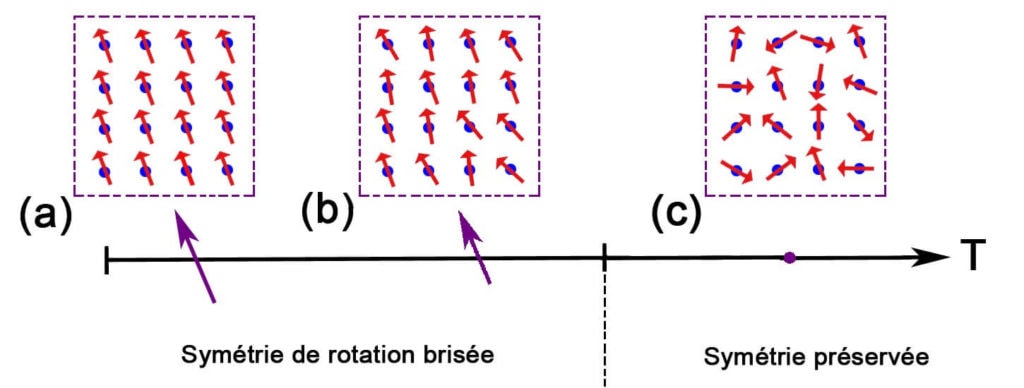
Afin d’aborder ce problème, l’auteur s’appuie sur une autre classification des phases de la matière : la symétrie. En physique, on définit ce concept en répondant à la question suivante : si je fais légèrement bouger/tourner/etc. les constituants microscopiques de l’échantillon, verrai-je une différence ? Si je n’en vois pas, c’est que le système physique est symétrique. Si je vois une différence, on dit que la symétrie est brisée (Figure 3).
On constate qu’une phase désordonnée (comme l’eau liquide ou la phase paramagnétique) correspond à une symétrie préservée, tandis qu’une phase ordonnée (comme la glace ou la phase ferromagnétique) correspond à une symétrie brisée [*]. La question « dans quelle phase le système physique que l’on étudie se trouve-t-il ? », peut donc se reformuler de la façon suivante : « le système physique a-t-il une symétrie brisée ? ». C’est à cette question que l’auteur veut répondre, dans le cas des films d’hélium liquide en 2D, sur la base d’un modèle issu de l’étude du magnétisme.
Première mi-temps : une approche (trop) simplifiée
Le modèle mathématique étudié par V. Berezinskii est appelé modèle XY 2D. Celui-ci décrit un ensemble de spins disposés sur un quadrillage à deux dimensions (d’où 2D), où l’on considère que chaque spin est comme une aiguille de boussole, c’est-à-dire qu’on le représente par une flèche contenue dans le plan du quadrillage, de longueur fixée, et pouvant pointer dans toutes les directions du plan (d’où l’appellation XY, par référence aux deux axes X et Y qui repèrent la direction du spin), comme ce que nous avons représenté sur les Figures 1 et 3. Les spins interagissent uniquement avec leurs voisins immédiats, et cette interaction tend à aligner chaque spin parallèlement à ses voisins : c’est l’interaction alignante. Bien que ce modèle n’ait pas été conçu pour étudier les films d’hélium liquide, on peut montrer qu’il est cependant approprié pour les décrire, c’est la magie de la modélisation !
Lorsque l’on place le matériau contenant les spins à une température donnée, les interactions alignantes (qui favorisent l’ordre) entrent en compétition avec les fluctuations thermiques, qui tendent, au contraire, à favoriser la symétrie en désalignant les spins. Alors, qui gagne ?
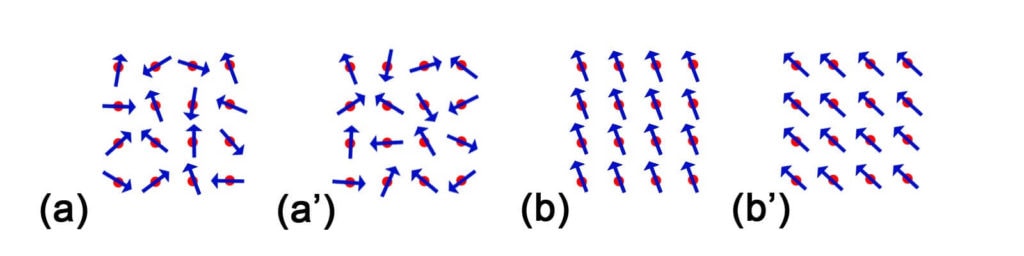
Une première approche simplifiée consiste à décrire comment, en moyenne, cette compétition entre les interactions alignantes et les fluctuations thermiques se manifeste à grande échelle. Les résultats de cette approche sont représentés en Figure 4. Celle-ci prédit l’existence :
- à basse température, d’une phase ordonnée (ferromagnétique) dans laquelle tous les spins s’alignent dans une même direction (rappel : Figure 3, il s’agit de la phase où la symétrie de rotation est brisée). En résumé, ce sont les interactions alignantes qui gagnent ;
- à haute température, d’une phase désordonnée (paramagnétique) : les spins pointent dans n’importe quelle direction avec la même probabilité, et fluctuent au gré des fluctuations thermiques (sur la Figure 3, il s’agit de la phase où la symétrie de rotation est préservée). En résumé, ce sont les fluctuations thermiques qui gagnent.
Ce résultat est très courant en physique, et en appliquant la démarche de l’auteur à d’autres modèles de cristaux, y compris 3D ou 1D, on obtiendrait le même résultat. À ce stade de la partie : l’ordre a marqué 1 point à basse température, la symétrie 1 point à haute température. En fait, dans les cristaux en 3D, le score n’évolue plus [2] ; mais il en va autrement aux plus basses dimensions.
Deuxième mi-temps : une approche plus précise
L’auteur nous met immédiatement en garde contre cette approche simplifiée, qui prédit une phase ordonnée à basse température. En effet, à cause des fluctuations thermiques, les spins peuvent en réalité osciller « légèrement » autour de leur position d’équilibre parfaitement alignée. On peut alors calculer l’amplitude de ces fluctuations, et constater qu’en dimensions 2 et 1, elles sont loin d’être petites ! En fait, l’hypothétique solution d’une phase ordonnée à basse température ne survit pas aux fluctuations thermiques, qui rétablissent la symétrie en ruinant l’ordre ! Bilan : +1 point pour la symétrie ! Dans les chaînes de spins — un peu comme si les spins étaient sur un collier de perles, c’est-à-dire à 1D — la partie s’achève ainsi sur une victoire de la symétrie par 2 buts à 1… mais tout n’est pas encore joué dans les systèmes bidimensionnels [3].
L’article de V. Berezinskii cherche à aller plus loin, en décrivant à quel point les spins sont désordonnés. En effet, si l’on considère un spin donné (au centre sur la Figure 5), on sait que si l’on s’éloigne suffisamment de lui, on trouvera des spins de toutes les orientations possibles, puisque l’on est dans une phase désordonnée. Toutefois, à cause de l’interaction alignante, on sait aussi que des spins proches voisins seront orientés de façon similaire. La question est donc : jusqu’à quelle distance l’interaction alignante fonctionne-t-elle ? Cette méthode s’avère fructueuse dans une phase désordonnée, où elle est un bon moyen de mesurer si le système de spins est soit très désordonné, soit au contraire quasi ordonné.
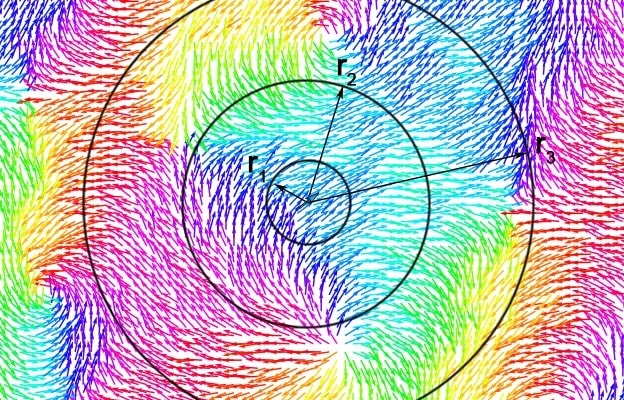
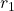 , les spins s’orientent presque tous dans une même direction ; en élargissant à
, les spins s’orientent presque tous dans une même direction ; en élargissant à 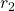 , on observe de plus en plus de différences d’orientations ; enfin, dans le cercle de rayon
, on observe de plus en plus de différences d’orientations ; enfin, dans le cercle de rayon 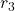 , les spins peuvent prendre des orientations très diverses qui sont presque indépendantes de celle du spin central. On se trouve donc dans une phase globalement désordonnée, avec un alignement à courte distance. Crédit : image modifiée à partir de ChrisJLygouras/Wikimédia Commons/CC BY-SA 4.0.
, les spins peuvent prendre des orientations très diverses qui sont presque indépendantes de celle du spin central. On se trouve donc dans une phase globalement désordonnée, avec un alignement à courte distance. Crédit : image modifiée à partir de ChrisJLygouras/Wikimédia Commons/CC BY-SA 4.0.Finalement, le calcul aboutit à un résultat en demi-teinte : les spins à basse température se trouvent dans une phase certes désordonnée à l’échelle globale… mais localement, celle-ci ressemble beaucoup à une phase ordonnée, avec des îlots de spins tous alignés entre eux (les taches de couleur de la Figure 5) qui peuvent être de très grande taille. Un peu comme dans une carte des vents au bulletin météo : à l’échelle de la planète, il existe des vents soufflant dans toutes les directions — phase globalement désordonnée —, mais localement il existe des régions où le vent souffle toujours dans une même direction, à l’échelle d’une région (comme le mistral dans le Languedoc) ou même d’un sous-continent (comme la mousson en Asie du Sud) — c’est un ordre local de longue portée.
À l’issue de cette deuxième mi-temps, on a vu que les films d’hélium liquide se trouvent toujours dans une phase désordonnée. On a aussi vu qu’à basse température (en pratique, en dessous de -271 °C environ), ce désordre ne se manifeste vraiment qu’aux grandes échelles. Alors c’est bon, on a tout compris ?
Fin de partie
En étudiant des films d’hélium à des température plus tièdes (moins de -269 °C tout de même ! au-dessus, l’hélium devient gazeux), les scientifiques ont constaté (comme on s’y attend depuis la première mi-temps) qu’ils se trouvent dans une phase très désordonnée. Il semble donc qu’il existe, quelque part, une température de transition, au-dessus de laquelle le désordre gagne la partie à toutes les échelles. Mais le mécanisme de cette transition reste mystérieux : l’article de V. Berezinskii n’apporte pas la réponse à cette question.
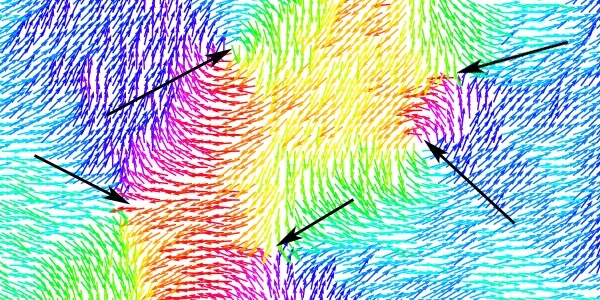
La solution viendra en fait deux ans plus tard, avec les travaux de Kosterlitz et Thouless [4], qui valurent à ces deux chercheurs le prix Nobel de physique 2016, trente-six ans après la mort de V. Berezinskii. Dans son article, celui-ci avait déjà mis le doigt sur le détail crucial : à haute température, les spins ont la possibilité de former des tourbillons (Figure 6) [**]. Ces tourbillons, en proliférant au fur et à mesure que la température augmente, détruisent les îlots de spins alignés et sont responsables de la transition vers la phase très désordonnée à haute température [5].
Cette transition de phase est remarquable car, contrairement à toutes les autres transitions connues jusqu’alors [1] (pensez, par exemple, à la fusion de la glace quand on augmente la température), il ne s’agit pas d’une transition entre une phase ordonnée où la symétrie est brisée (comme la glace), et une phase désordonnée où la symétrie est préservée (comme l’eau liquide). La rencontre qui devait se jouer, comme d’habitude, entre la symétrie et l’ordre, est en fait bouleversée par l’arrivée d’une troisième équipe : les tourbillons. En résumé, l’ordre subit effectivement une défaite dans les films d’hélium liquide, mais la victoire n’est pas remportée par la symétrie : ce sont les tourbillons qui volent la coupe !
[*] Maintenant que vous avez tout compris, petite devinette : dans la première image de cet article, lequel des deux personnages représente la symétrie et lequel représente ordre ? Réponse : [#]
[**] Notons que dans un film d’hélium liquide, ce sont de véritables tourbillons, correspondant à un écoulement de fluide bien réel ! Ces tourbillons sont la manifestation d’un ingrédient physique devenu un incontournable de la physique de la matière condensée : la topologie.
[#] Réponse : la symétrie est à gauche, avec son maillot uniforme où le bleu et le blanc sont parfaitement mélangés, et son ballon gris uniforme parfaitement symétrique également. L’ordre est à droite, avec son maillot où le bleu et le blanc sont bien séparés et alternent périodiquement, et son ballon où les taches noires forment une structure bien ordonnée qui ressemble à un cristal.
[1] Landau L. D., « On the Theory of Phase Transitions ». Journal of Experimental and Theoretical Physics, 1937. In : Collected papers of L.D. Landau. ISBN : 9780080105864. [Livre de science]
[2] Villain J., La structure des substances magnétiques. Journal of Physics and Chemistry of Solids, 1959, DOI : 10.1016/0022-3697(59)90231-8. [Publication scientifique, mâchée ici]
[3] Mermin N. D. & Wagner H., Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Physical Review Letters, 1966. DOI : 10.1103/PhysRevLett.17.1133. [Publication scientifique]
[4] Kosterlitz J. M. & Thoules D. J., Ordering, metastability and phase transitions in two-dimensional systems. Journal of Physics C: Solid State Physics, 1973. DOI : 10.1088/0022-3719/6/7/010. [Publication scientifique]
[5] Goldenfeld N., « Lectures On Phase Transitions And The Renormalisation Group », Ed. Westview Press, Boulder (CO), 1992. ISBN : 978-0201554090. [Livre de science]
Écriture : Léo Mangeolle
Relecture scientifique : Dorian Vigoureux et Éric Brillaux
Relecture de forme : Aurélien Didier
Temps de lecture : environ 16 minutes.
Thématiques : Matière condensée (Physique)
Publication originale : Berezinskii V. L., Destruction of Long-range Order in One-dimensional and Two-dimensional Systems having a Continuous Symmetry Group I. Classical Systems. Journal of Experimental and Theoretical Physics, 1971.

Pourquoi, à basse température, l’eau se change-t-elle en glace ? La réponse à cette question repose sur les concepts d’ordre et de symétrie. Pour décider de l’état dans lequel se trouvera la matière, un match se joue en effet entre la symétrie et l’ordre, en fonction des conditions dans lesquelles le système se trouve, et en particulier de la température ambiante. Dans son article de 1971, V. Berezinskii explore le rôle d’un autre paramètre important, la dimension, en se focalisant sur celle où la physique est la plus étonnante : la dimension 2.
L’enjeu de la rencontre
Une des missions de la physique moderne est de comprendre et de classifier les différentes phases de la matière. Ce terme désigne une configuration d’un système physique, n’existant éventuellement que dans certaines conditions physiques particulières (température, pression, champ magnétique extérieur, etc.), et présentant des caractéristiques homogènes à l’échelle macroscopique ; cette définition comprend notamment :
- les différents états d’un corps pur (liquide, gaz, cristal, etc.) qui correspondent à l’agencement des atomes ou des molécules dans l’espace ;
- les différentes structures magnétiques (paramagnétique, ferromagnétique, etc.) qui correspondent à l’organisation des spins dans un matériau ;
- bien d’autres exemples de phases, pouvant correspondre à l’organisation des charges électriques dans un solide, à celle des différents ingrédients dans une vinaigrette, ou encore à la distribution des vitesses dans un banc de poissons.
Pour beaucoup de ces phases, il est possible de les classer en deux catégories. D’une part, les phases ordonnées, comme les cristaux (où les atomes sont régulièrement espacés selon une structure géométrique) ou la phase ferromagnétique (où les spins sont tous alignés dans une seule direction) — tout ceci en première approximation, sans tenir compte des petites fluctuations autour de cette configuration d’équilibre qui peuvent être d’origine thermique ou quantique. D’autre part, les phases désordonnées, comme les liquides (où les atomes n’ont pas de place assignée et peuvent bouger les uns par rapport aux autres) ou la phase paramagnétique (où l’orientation des spins peut fluctuer dans toutes les directions). La notion d’ordre permet donc de réaliser cette première classification.
L’une des grandes réussites de la physique du XXe siècle (voir notamment [1]) a été de mettre cette notion d’ordre en opposition à celle de symétrie, réalisant ainsi une deuxième classification des différentes phases de la matière. Par exemple, si l’on considère un atome seul dans l’espace, à la position ![]() , celui-ci est libre de se translater à une position
, celui-ci est libre de se translater à une position ![]() un peu plus loin : la position
un peu plus loin : la position ![]() n’a « rien de spécial ». Maintenant, si l’on met des milliards de tels atomes ensemble, deux cas de figure peuvent se présenter :
n’a « rien de spécial ». Maintenant, si l’on met des milliards de tels atomes ensemble, deux cas de figure peuvent se présenter :
- Les atomes forment un liquide : leur symétrie de translation est préservée, et la position d’un atome n’a toujours « rien de spécial » : si je vous montre une photo d’une piscine à balles que j’ai retouchée pour subrepticement décaler une balle, vous ne vous rendrez compte de rien.
- Ils s’arrangent sous forme de cristal, et un atome n’a plus le droit de se décaler dans l’espace comme bon lui semble. On dit que la symétrie de translation est brisée : si je vous montre une photo d’un carrelage où j’ai légèrement déplacé un carreau, cela se verra tout de suite.
On voit sur cet exemple, et cela peut se généraliser, qu’une phase désordonnée (ici, le liquide) correspond à une symétrie préservée, tandis qu’une phase ordonnée (ici, le cristal) correspond à une symétrie brisée. Voir Figure 1 pour l’équivalent dans un cristal magnétique. La question « dans quelle phase le système physique que l’on étudie va-t-il se trouver ? » peut donc se reformuler de la façon suivante : « la symétrie va-t-elle être brisée ? ». C’est à cette question que l’article de Berezinskii cherche à répondre.

Plus particulièrement, la publication s’intéresse à un cas assez particulier, les systèmes à deux dimensions. On peut penser, par exemple, à un film d’hélium liquide, qui est probablement la principale préoccupation de l’auteur. Le cas de la dimension 2 est très particulier car, d’une part, les expériences sur les films d’hélium (plus précisément, d’hélium 4 à très basse température avec T < 4 K) conduisaient à des résultats physiques nouveaux qui n’apparaissaient pas dans des échantillons à trois dimensions. D’autre part, il représentait un mystère théorique car, pour un même problème, des approches mathématiques différentes donnent des résultats antagonistes, avec d’un côté les approches de champ moyen [2], intuitivement raisonnables bien qu’approximatives, qui prédisent l’existence d’une phase ordonnée à basse température, et de l’autre, le théorème de Mermin-Wagner [3], mathématiquement rigoureux mais peu accessible à l’intuition, qui prédit qu’une telle phase ordonnée ne peut pas exister.
L’objectif de l’article de Berezinskii est donc, principalement, de donner une interprétation physique au résultat du théorème de Mermin-Wagner qui prédit la victoire de la symétrie sur l’ordre en dimension 2, et accessoirement, de lever un peu le voile sur la physique mystérieuse des films d’hélium liquide.
Première mi-temps : le modèle XY, version « champ moyen »
Le modèle mathématique que l’article étudie est un modèle d’interactions magnétiques appelé modèle XY 2D. Il décrit un cristal magnétique à deux dimensions, sur réseau carré, où le spin de chaque atome est comme une aiguille de boussole, c’est-à-dire qu’on le représente par une flèche contenue dans le plan du cristal, de longueur fixée, et donc entièrement caractérisée par l’angle qu’elle forme par rapport à un axe donné. Les spins y sont décrits classiquement, c’est-à-dire que les effets de la mécanique quantique ne sont pas pris en compte ; cela est justifié par le fait que V. Berezinskii cherche à mettre en évidence des phénomènes qui apparaissent aussi dans un cadre purement classique (on verra que les phénomènes importants pour comprendre la physique des films d’hélium liquide se produisent sur de grandes échelles de distance, où les effets de la physique quantique s’expriment généralement peu).
On peut aussi noter que, malgré l’apparente déconnexion entre ce problème d’ordre magnétique dans un cristal d’une part, et la physique d’un film d’hélium liquide d’autre part, ces deux problèmes sont en fait reliés par leurs symétries. Dans le cas présent, l’orientation de chaque « spin-boussole » est entièrement décrite par un angle entre 0° et 360° ; la symétrie qui peut donc être brisée est la symétrie de rotation : « est-ce que cela se remarquerait si je tournais ce spin-là de quelques degrés vers la gauche ? ». Tandis que dans les films d’hélium liquide, le paramètre d’ordre, dit superfluide, est plus subtil et n’a absolument rien à voir avec une quelconque boussole, mais est aussi un angle entre 0° et 360° (il s’agit de l’argument d’un nombre complexe caractérisant localement le fluide). Cela signifie qu’on peut en apprendre beaucoup sur les films d’hélium liquide en s’intéressant au modèle XY 2D.
Enfin, dans ce modèle, les spins interagissent uniquement avec leurs voisins immédiats, et l’interaction est de nature alignante (c’est-à-dire qu’elle favorise un spin aligné parallèlement à ses voisins). Pour se faire une première idée de l’ordre magnétique qui naîtra de la compétition entre l’énergie d’interaction et l’agitation thermique, l’article suggère de s’intéresser à l’énergie libre, qui est une grandeur macroscopique décrivant le système physique à l’équilibre à une température fixée. Pour calculer cette grandeur à partir du modèle microscopique dont on dispose, plusieurs méthodes sont envisagées.
La plus simple, d’abord, est l’approximation dite de champ moyen (voir [2]), qui consiste à considérer qu’un spin donné tend à s’aligner avec la direction moyenne de l’ensemble des spins. Les résultats de cette approche sont représentés en Figure 2. Celle-ci prédit l’existence :
- à basse température [*], d’une phase ordonnée ferromagnétique dans laquelle tous les spins s’alignent dans une même direction (à de faibles fluctuations près autour de cette position d’équilibre). Or, a priori, n’importe quel axe peut servir de direction d’alignement moyen : en adoptant une orientation privilégiée plutôt qu’une autre, les spins brisent la symétrie de rotation ;
- à haute température [*], d’une phase désordonnée paramagnétique : les spins pointent dans n’importe quelle direction avec la même probabilité, et fluctuent au gré de l’agitation thermique (la symétrie de rotation est préservée).
À ce stade de la partie : l’ordre a marqué 1 point à basse température, la symétrie 1 point à haute température. Dans les cristaux 3D, le score n’évolue plus ; mais il en va autrement aux plus basses dimensions.
Deuxième mi-temps : le modèle XY, version « corrélations »
L’auteur nous met immédiatement en garde contre cette approche de champ moyen, qui prédit une phase ordonnée à basse température. Pour ce faire, il effectue un raisonnement par l’absurde : supposons qu’il existe effectivement une telle phase ordonnée ferromagnétique, où les spins s’alignent tous dans la même direction. Si maintenant on tient compte des fluctuations thermiques, les spins peuvent osciller légèrement autour de leur position d’équilibre parfaitement alignée ; on peut alors se demander quelle est la quantité d’énergie qui est emmagasinée dans ces petites oscillations. Il se trouve que cette grandeur dépend beaucoup de la dimension du système, et donne des résultats beaucoup plus grands en basse dimension (où, de manière assez générale, l’agitation thermique l’emporte sur l’énergie d’interaction) ; en dimensions 2 et 1, on tombe en fait sur une énergie infinie ! La conclusion de cette preuve par l’absurde est que l’hypothétique solution ordonnée ne survit pas aux fluctuations thermiques, aussi basse que puisse être la température. +1 point pour la symétrie. Dans les chaînes de spins (c’est-à-dire à 1D), la partie s’achève généralement sur une victoire de la symétrie par 2 buts à 1… mais tout n’est pas encore joué dans les systèmes bidimensionnels.
En effet, maintenant que l’on sait que le système se trouve dans une phase désordonnée à basse température, on peut se demander à quoi elle ressemble. La seule phase désordonnée que prédit l’approximation de champ moyen est paramagnétique, c’est-à-dire que les spins peuvent être traités d’un point de vue macroscopique comme s’ils étaient indépendants les uns des autres ; mais on ne sait rien de leur organisation à l’échelle microscopique. Alors comment faire ? La méthode de l’article consiste à calculer ce qu’on appelle la fonction de corrélation entre les spins. L’idée (voir Figure 3) est la suivante : si l’on considère un spin donné (au centre sur la figure), on sait que ses voisins proches auront des orientations très similaires (on dira que leur corrélation est forte), à cause de l’interaction alignante. On sait aussi que si l’on s’éloigne suffisamment, on trouvera des spins de toutes les orientations possibles, puisqu’on est dans une phase désordonnée (on dira alors que leur corrélation avec le spin central est faible). La fonction de corrélation permet de décrire l’évolution de cette corrélation au fur et à mesure que l’on s’éloigne du spin central ; plus cette fonction décroît lentement, plus la phase est ordonnée. Dans une phase ordonnée ferromagnétique, la fonction de corrélation est même constante : les spins sont toujours fortement corrélés quelle que soit l’échelle à laquelle on se place. L’étude de la fonction de corrélation est fructueuse dans une phase désordonnée, où elle est un bon moyen de mesurer si le système de spins est très désordonné (la corrélation décroît rapidement avec la distance), ou au contraire quasi-ordonné (la corrélation décroît lentement avec la distance).
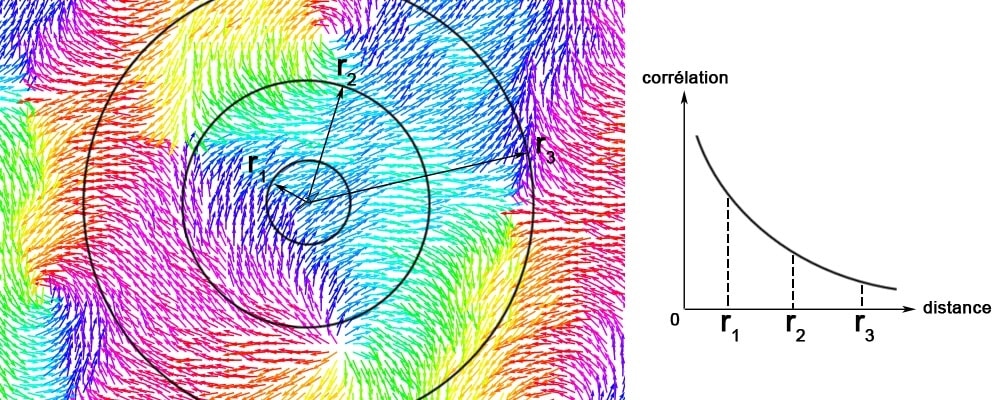
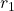 les spins se ressemblent tous (forte corrélation) ; en élargissant à
les spins se ressemblent tous (forte corrélation) ; en élargissant à 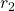 on observe de plus en plus de différences (la corrélation diminue) ; enfin, dans le cercle de rayon
on observe de plus en plus de différences (la corrélation diminue) ; enfin, dans le cercle de rayon 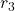 les spins peuvent prendre des orientations très diverses qui sont très peu corrélées avec celle du spin central (faible corrélation). Le fait que la fonction de corrélation soit décroissante indique que l’on se trouve dans une phase désordonnée. Crédit : image modifiée à partir de ChrisJLygouras/Wikimédia Commons/CC BY-SA 4.0.
les spins peuvent prendre des orientations très diverses qui sont très peu corrélées avec celle du spin central (faible corrélation). Le fait que la fonction de corrélation soit décroissante indique que l’on se trouve dans une phase désordonnée. Crédit : image modifiée à partir de ChrisJLygouras/Wikimédia Commons/CC BY-SA 4.0.Pour effectuer son calcul, V. Berezinskii se place dans un régime de basse température, afin que les fluctuations thermiques ne soient pas trop grandes et que l’on puisse traiter les fluctuations d’alignement des spins comme de faibles corrections à l’alignement entre spins voisins. Il souligne l’importance de cette hypothèse : si les fluctuations étaient trop grandes, il serait difficile de faire la différence entre une fluctuation de 350° vers la droite ou de 10° vers la gauche… La possibilité que les spins puissent effectuer un « tour complet » sur de courtes distances est une complication qui apparaît à plus haute température (où des fluctuations suffisamment grandes sont permises), et peut être négligée en première approximation.
Finalement, le calcul aboutit à un résultat en demi-teinte : la fonction de corrélation décrit une phase certes désordonnée (la corrélation décroît), mais avec des corrélations à grande distance (elle décroît lentement). En fait, tout comme dans une phase ferromagnétique, il n’existe pas de longueur typique de corrélation, c’est-à-dire de rayon ![]() tel que l’on puisse dire : « si on regarde dans un rayon
tel que l’on puisse dire : « si on regarde dans un rayon ![]() autour d’un spin donné
autour d’un spin donné ![]() , on trouvera certainement un spin
, on trouvera certainement un spin ![]() orienté dans la direction opposée à
orienté dans la direction opposée à ![]() ». Ce sera parfois le cas, mais parfois tous les spins situés dans un rayon
». Ce sera parfois le cas, mais parfois tous les spins situés dans un rayon ![]() autour du spin
autour du spin ![]() seront orientés presque dans la même direction que
seront orientés presque dans la même direction que ![]() , et il faudra aller beaucoup plus loin pour trouver un spin
, et il faudra aller beaucoup plus loin pour trouver un spin ![]() pointant dans la direction opposée. La phase de basse température est donc une phase désordonnée (la symétrie de rotation y est globalement préservée), mais localement elle ressemble à une phase ordonnée ferromagnétique, avec des îlots ordonnés (les taches de couleur de la Figure 3) qui peuvent être arbitrairement vastes. À l’issue de cette deuxième mi-temps, la symétrie l’emporte donc sur l’ordre, mais de justesse (il aura fallu jouer les prolongations !). À moins que…
pointant dans la direction opposée. La phase de basse température est donc une phase désordonnée (la symétrie de rotation y est globalement préservée), mais localement elle ressemble à une phase ordonnée ferromagnétique, avec des îlots ordonnés (les taches de couleur de la Figure 3) qui peuvent être arbitrairement vastes. À l’issue de cette deuxième mi-temps, la symétrie l’emporte donc sur l’ordre, mais de justesse (il aura fallu jouer les prolongations !). À moins que…
Fin de partie
Les calculs de l’article s’appliquent à la phase désordonnée dans un régime de basse température, et aboutissent à des corrélations de longue portée. Mais d’autres études, qui se sont intéressées à la phase désordonnée à haute température grâce à des simulations numériques, indiquent que les corrélations y sont de courte portée [4]. Autrement dit, cette phase est plutôt très désordonnée. Il semble donc qu’il existe, quelque part entre les deux, une température de transition où l’on passe d’un régime à l’autre par un mécanisme qu’il reste à élucider.
La fin de l’article consiste à montrer que ce phénomène est très général et s’applique à tous les systèmes 2D où il existe une symétrie continue qui risque d’être brisée (dans le modèle XY il s’agit de la symétrie de rotation, mais les autres symétries continues présentent en fait le même comportement). Mais le mécanisme de la transition reste mystérieux : l’article n’apporte pas la réponse à cette question.

Dans le cas du modèle XY, la solution viendra en fait deux ans plus tard, avec les travaux de Kosterlitz et Thouless [5][**]. Dans son article, Berezinskii avait déjà mis le doigt sur le détail qui tue : à haute température, les spins ont la possibilité d’effectuer des tours complets sur de courtes distances, en formant ainsi des tourbillons (Figure 4). Notons que même si, dans le modèle XY, ce sont des tourbillons statiques dessinés par les spins dans le plan, dans un film d’hélium liquide ce sont de véritables tourbillons correspondant à un écoulement de fluide ! Ce sont ces tourbillons qui, en proliférant au fur et à mesure que la température augmente, détruisent les corrélations à longue portée et sont responsables de la transition vers la phase très désordonnée à haute température [6].
Cette transition de phase est remarquable car, contrairement à toutes les autres transitions connues jusqu’alors [1], il ne s’agit pas d’une transition entre une phase ordonnée, où la symétrie est brisée, et une phase désordonnée, où la symétrie est préservée. La rencontre qui devait se jouer, comme d’habitude, entre la symétrie et l’ordre, est en fait bouleversée par l’arrivée d’une troisième équipe — qui porte le nom de topologie, et est matérialisée ici par les tourbillons — qui est devenue, depuis, un acteur incontournable de la physique de la matière condensée. Alors, match nul ?
[*] La température qui marque la transition entre les deux régimes, basse et haute température, est appelée de façon générique température critique. Dans le cas des transitions ordre/désordre dans les cristaux magnétiques, on parlera de température de Curie ou de température de Néel, et en fonction du matériau celles-ci peuvent prendre des valeurs entre quelques kelvin et plus de ![]() K. Dans le cas de la transition hélium liquide/superfluide, la température critique vaut 2,17 K.
K. Dans le cas de la transition hélium liquide/superfluide, la température critique vaut 2,17 K.
[**] Cette découverte, connue sous le nom de « Transition de Berezinskii-Kosterlitz-Thouless », valut à ces deux derniers le prix Nobel de physique en 2016, trente-six ans après la mort de V. Berezinskii.
[1] Landau L. D., « On the Theory of Phase Transitions ». Journal of Experimental and Theoretical Physics, 1937. In : Collected papers of L.D. Landau. ISBN : 9780080105864. [Livre de science]
[2] Villain J., La structure des substances magnétiques. Journal of Physics and Chemistry of Solids, 1959, DOI : 10.1016/0022-3697(59)90231-8. [Publication scientifique, mâchée ici]
[3] Mermin N. D. & Wagner H., Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Physical Review Letters, 1966. DOI : 10.1103/PhysRevLett.17.1133. [Publication scientifique]
[4] Jorge V. J., et al., Renormalization, vortices, and symmetry-breaking perturbations in the two-dimensional planar model. Physical Review B, 1977. DOI : 10.1103/PhysRevB.16.1217. [Publication scientifique]
[5] Kosterlitz J. M. & Thoules D. J., Ordering, metastability and phase transitions in two-dimensional systems. Journal of Physics C: Solid State Physics, 1973. DOI : 10.1088/0022-3719/6/7/010. [Publication scientifique]
[6] Goldenfeld N., « Lectures On Phase Transitions And The Renormalisation Group », Ed. Westview Press, Boulder (CO), 1992. ISBN : 978-0201554090. [Livre de science]

Bonjour,
On dit souvent que plus on est proche du « big bang »,plus l’Univers était ordonné, en effet l’entropie d’un système fermé ne fait qu’augmenter.
Comment se fait-il que l’Univers proche du « big bang » ressemblait plus à l’etat de gauche des joueurs de foot, très symétrique,(ballon gris), la matière étant même non découplée de la lumière, si très symétrique = très désordonnée,alors que justement elle était le plus ordonné que jamais après ?
PS j’ai posé la question à chatGPT qui m’a répondu que l’univers n’était pas un système fermé ,et suite à mon interrogation = si pas fermé sur quoi est il ouvert ? M’a répondu = sur le vide.
Est ce la réponse? J’ai du mal à accepter cette réponse,S’agirait il du vide quantique ?
Ou bien quelle serait la réponse à ma question sur cet (apparent?) paradoxe?
Merci !