Chargement de l'article...
Écriture : Léo Mangeolle
Relecture scientifique : Léa Lachaud
Relecture de forme : Tristan Guyomar et Agathe Pralus
Temps de lecture : environ 11 minutes.
Thématique : Matière condensée (Physique)
Publication originale : Villain J., La structure des substances magnétiques. Journal of Physics and Chemistry of Solids, 1959. DOI : 10.1016/0022-3697(59)90231-8
De nombreuses technologies modernes comme les IRM, le stockage sur disque dur ou encore les hauts-parleurs utilisent des aimants. Aussi appelés cristaux magnétiques, ces matériaux présentent une très grande variété de structures internes, en réponse aux contraintes dictées par les interactions entre les aimantations de tous les atomes du cristal. Les règles du jeu sont assez simples : les aimantations de deux atomes voisins doivent former un angle le plus proche possible d’une consigne (généralement, être alignées ↑↑ ou anti-alignées ↑↓), dictée notamment par la nature chimique du cristal et par sa géométrie. Mais le jeu reste complexe : si l’aimantation d’un atome doit s’anti-aligner avec ↑,←,↓ et → en même temps, quelle orientation choisir ? Comment trouver une solution à l’amiable qui satisfasse tous les atomes du cristal ? C’est ce problème diplomatique complexe que Jacques Villain a cherché à résoudre en 1959, afin d’expliquer comment des solutions globales très diverses peuvent émerger à partir de quelques règles d’interaction locales simples.
Que cherche-t-on à résoudre au juste ?
Quand on joue avec un aimant, on sait juste que c’est un morceau de fer qui est globalement aimanté. Mais d’où provient cette aimantation à l’échelle microscopique ? Depuis le début du XXe siècle, on sait que chaque atome de l’aimant possède sa propre aimantation locale (on utilisera le terme impropre [*] mais couramment utilisé de spin dans la suite), et l’aimantation globale du morceau de fer s’explique alors par le fait que tous les spins des atomes s’alignent dans une même direction. Mystère résolu. Mais clairement, tous les aimants ne sont pas en fer, et tous les métaux ne collent pas à la porte du frigo ! L’aluminium, par exemple, n’est pas naturellement aimanté.
En fait, des comportements très divers ont pu être identifiés, comme le ferromagnétisme (comme celui d’un aimant en fer, qui possède sa propre aimantation, permanente dans le temps) et le paramagnétisme (comme celui d’un morceau d’aluminium, qui n’a pas d’aimantation propre mais peut s’aimanter temporairement si on l’approche d’un aimant), mais aussi beaucoup d’autres, plus compliqués. À chaque comportement macroscopique (= observable à l’œil nu) correspond un agencement microscopique des spins, assimilés dans la publication à des flèches microscopiques pouvant pointer dans n’importe quelle direction. C’est cette structure microscopique, en général inconnue, que J. Villain cherche à prédire dans son article.
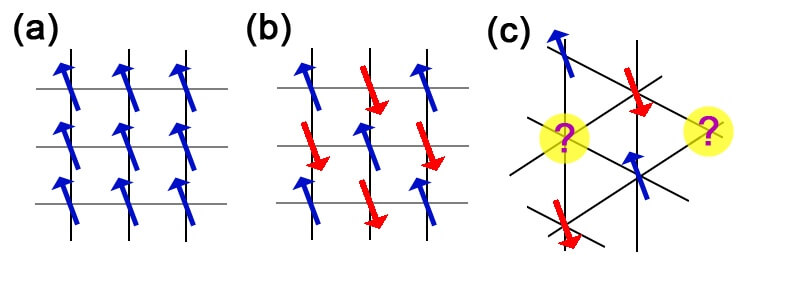
La publication s’attaque simultanément à toute une variété d’interactions : non seulement des interactions entre atomes voisins, mais aussi entre des atomes arbitrairement éloignés dans le cristal. La nature de ces interactions (alignantes, anti-alignantes, ou autres) dépend de nombreux paramètres, notamment de la nature chimique des atomes impliqués, de la géométrie précise du cristal (qui elle-même peut dépendre de la température, de la pression, etc.), de la présence d’autres atomes à proximité, ou encore d’un champ magnétique extérieur, etc. Bref, déterminer ces interactions est un sujet en soi, mais ce n’est pas celui de l’article — ce dernier s’attelle plutôt à déduire des comportements à grande échelle à partir de ces règles d’interaction microscopiques supposées connues. Ainsi, à basse température, c’est-à-dire lorsque l’agitation thermique ne vient pas perturber l’orientation des spins, ces interactions donnent lieu à diverses configurations possibles : quand les voisins immédiats tendent à aligner leurs spins, on s’attend à du ferromagnétisme (Figure 1a) ; quand ils tendent à les anti-aligner, sur réseau carré on s’attend à de l’antiferromagnétisme (= propriété observée lorsque chaque spin est aligné dans la direction opposée à ses voisins immédiats) (Figure 1b), mais pour un réseau triangulaire, à quoi s’attendre ? La Figure 1c montre qu’une solution antiferromagnétique n’est pas satisfaisante, car alors un tiers des spins ne sait pas sur quel pied danser : faut-il s’anti-aligner avec les bleus (au prix de devoir s’aligner avec les rouges), ou le contraire ? Ou ni l’un ni l’autre ? C’est notamment à cette question que l’article apporte une réponse.
L’approche de champ moyen
Pour résoudre ce problème de voisinage, l’article utilise une approche calculatoire simplifiée dite de champ moyen, bien connue depuis 1907 (publication de Weiss développant cette approche [1]), qui consiste à ne pas s’intéresser aux détails individuels des quelques millions de milliards de milliards d’atomes qui constituent le cristal, mais de les étudier seulement en moyenne. Le résultat permet de distinguer deux comportements distincts. Selon que le cristal est à une température supérieure ou inférieure à une température particulière, dite température critique (que l’approche adoptée dans l’article permet de calculer), deux comportements radicalement différents (on parle de phases) sont observés :
- À haute température, l’agitation thermique domine les interactions et on observe une phase désordonnée, où à chaque instant il y a en moyenne autant de spins pointant dans une direction que dans la direction opposée, et tous les spins se retournent sans arrêt au gré des fluctuations thermiques. On est alors dans la phase dite paramagnétique : les spins n’ont pas réussi à s’accorder pour construire une aimantation globale, et le cristal n’a pas d’aimantation propre.
- À l’inverse, à basse température, ce sont les interactions entre les spins qui dominent, et on observe une phase ordonnée, figée dans le temps à l’abri des fluctuations thermiques. Dans cette phase dite ferromagnétique, le cristal peut avoir une aimantation propre, car les spins ont trouvé leur solution de compromis, dont la structure précise dépend bien sûr des règles d’interaction entre spins voisins.
Par exemple, pour un aimant en fer, la température critique est de 770°C [2] ; à température ambiante, on se trouve donc bien dans la phase ordonnée, et le fer présente une aimantation globale qui lui permet de coller à la porte du frigo.
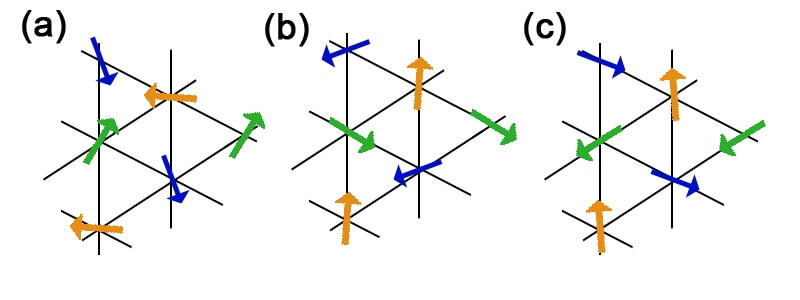
On sait maintenant qu’il existe une phase ordonnée à basse température. La principale question à laquelle il reste à répondre est : à quoi ressemble cette phase ordonnée ? Le résultat principal de l’article est justement une réponse sous forme de modélisation mathématique : l’auteur présente une formule générale qui donne la solution optimale pour tout système de spins, quelles que soient les règles d’interaction. On retrouve d’une part avec cette formule des résultats déjà pressentis plus haut dans cet article, comme le ferromagnétisme ou l’antiferromagnétisme (voir Figure 1). Mais la formule obtenue par J. Villain permet également d’obtenir des résultats moins évidents comme, par exemple, la solution au problème de répulsion de plus proches voisins sur le réseau triangulaire : il s’agit de la solution dite 120 degrés : c’est-à-dire que les directions des spins de deux atomes voisins forment toujours un angle de 120° entre elles (voir Figure 2). On voit d’ailleurs que la solution n’est pas unique : il peut y avoir plusieurs solutions, voire une infinité.
Ce résultat est-il satisfaisant ?
La solution donnée par l’article pour la phase ordonnée est celle qui, schématiquement, minimise le mécontentement général : c’est une solution de compromis. On peut donc se demander si la structure magnétique ne risque pas de se désordonner spontanément, si des spins rebelles décidaient d’améliorer leur sort individuel au détriment du bien-être général. On peut vérifier cela par le calcul ; verdict : tout va bien ! La solution apportée par J. Villain correspond systématiquement à la configuration optimale, ce qui signifie que même sous l’effet d’une fluctuation, aucun spin n’a intérêt à s’orienter différemment puisqu’il est déjà dans la configuration la plus satisfaisante pour lui. De plus, cette solution ordonnée stable ne dépend pas de la température, et reste la solution optimale jusqu’à la température critique, comme cela est observé par exemple dans le cas du ferromagnétisme. En outre, on sait par l’expérience que de très nombreux cristaux magnétiques s’ordonnent effectivement à basse température : la solidité du résultat est donc en prime confirmée par l’expérience (du moins, dans de nombreux cas).
Quelles structures peut-on espérer rencontrer ?
On sait donc que la solution obtenue dans la publication est une bonne solution stable, pour des règles d’interaction et une structure cristalline données. On peut maintenant essayer d’anticiper les expériences : quelles structures magnétiques peuvent, a priori, apparaître si l’on explore différentes règles du jeu (par exemple avec des simulations numériques), en faisant varier les paramètres géométriques du cristal, les atomes présents, etc. ?
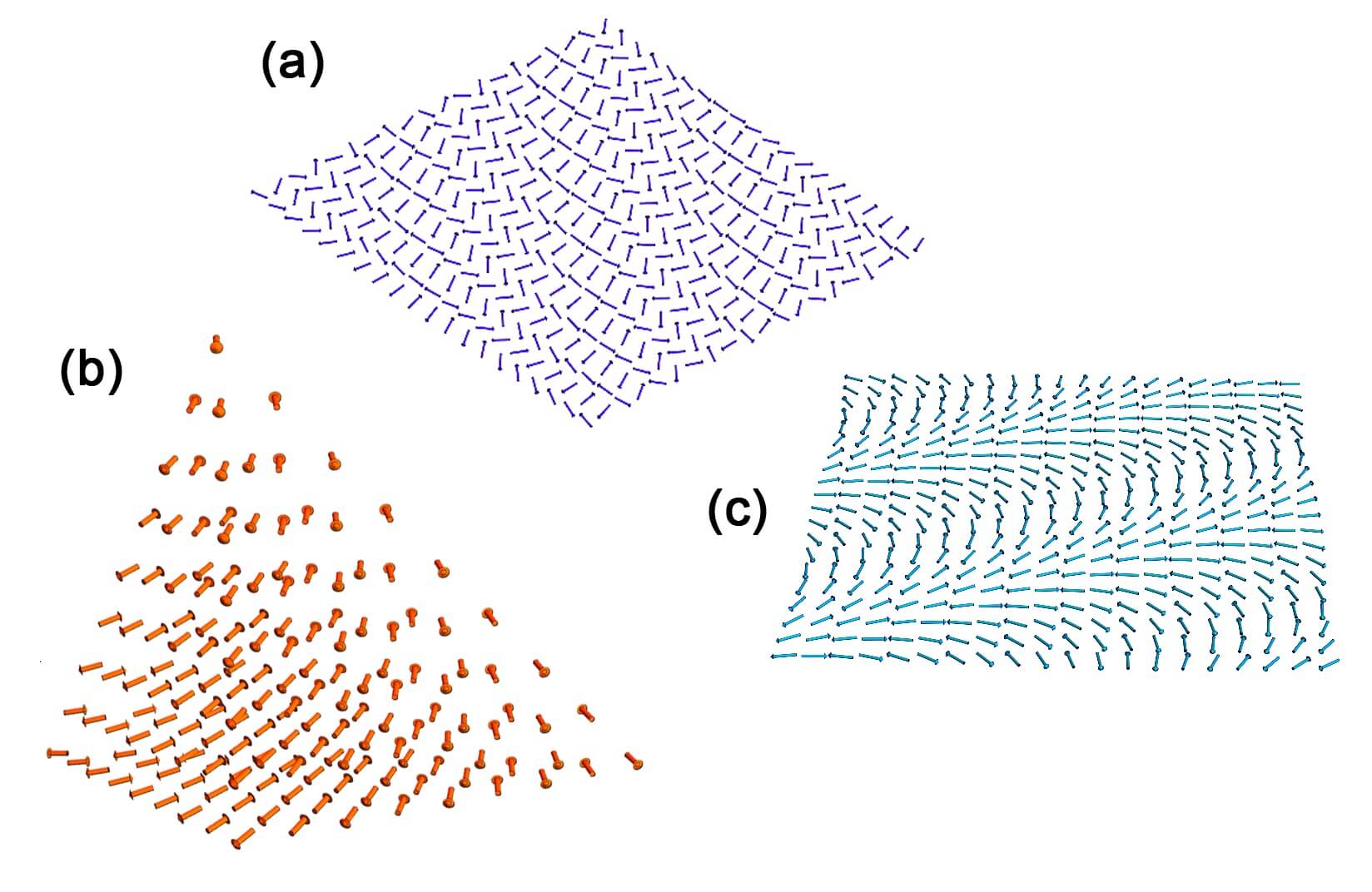
Une propriété générale : la solution trouvée est toujours périodique, c’est-à-dire que, comme un carrelage, il s’agit d’un même motif qui se répète indéfiniment dans tout le cristal. C’est évidemment le cas pour la Figure 1a et Figure 1b, mais aussi pour des solutions moins évidentes comme la solution 120 degrés de la Figure 2. À première vue, c’est peut-être décevant car cela restreint légèrement les possibilités, mais c’est en fait un résultat très enthousiasmant, puisqu’il laisse la porte ouverte à toute une variété de structures magnétiques nouvelles (et plutôt jolies, voir Figure 3) : des structures hélicoïdales par exemple !
Quel intérêt aujourd’hui ?
À lire cet article, on pourrait croire que la recherche sur le magnétisme a atteint son but ultime en 1959, avec une compréhension universelle de tous les cristaux magnétiques. C’est en fait loin d’être le cas, car de nombreux matériaux présentent — à basse température surtout — des propriétés bien plus bizarres qu’une simple structure ordonnée ! La solution apportée par J. Villain au problème de cohabitation des spins dans les cristaux magnétiques n’est donc pas la fin de l’histoire, puisqu’elle ne permet pas d’expliquer ces propriétés inhabituelles. Le modèle utilisé dans la publication s’avère alors insuffisant car il est basé sur une approximation : considérer les spins comme des flèches microscopiques de longueur et de position bien définies, en oubliant d’utiliser la mécanique quantique qui est l’outil approprié pour étudier le magnétisme à l’échelle microscopique.
L’auteur adopte donc une approche volontairement simplifiée qui permet de mener les calculs jusqu’au bout, là où une approche quantique plus exacte nécessiterait des calculs extrêmement compliqués, trop coûteux pour les ordinateurs actuels. Toutefois, bien que la formule de Villain ne donne qu’une approximation de la véritable structure magnétique microscopique, c’est un premier outil parfois très utile ! Par exemple pour l’étude des ondes de spin : si l’on veut étudier les petites oscillations des spins autour de leur position d’équilibre, la moindre des choses est de connaître ladite position d’équilibre, et cet article apporte à ce problème une solution peut-être imparfaite, mais prête à l’emploi.
D’autre part, la recherche actuelle en physique de la matière condensée s’intéresse beaucoup aux cas où l’approche de l’article ne fonctionne pas du tout, ce qui peut arriver lorsque la dimension effective du matériau étudié n’est pas 3, mais plutôt 2 (des matériaux en couches) ou 1 (certains matériaux constitués de chaînes d’atomes parallèles). Dans ces cas-là, la solution de l’article ne ressemble pas du tout à ce que l’on constate expérimentalement : il faut donc absolument revoir le modèle pour tenir compte des phénomènes quantiques à l’œuvre.
[*] Le terme de spin est ici impropre car il renvoie ici à l’aimantation totale de l’atome, alors que stricto sensu, un spin correspond à une particule élémentaire.
[1] Weiss P., L’hypothèse du champ moléculaire et la propriété ferromagnétique. J. Phys. Theor. Appl., 1907. DOI : 10.1051/jphystap:019070060066100. [Publication scientifique]
[2] Wikipédia, Température de Curie.
Paramagnétisme, ferromagnétisme, antiferromagnétisme. What else?
Écriture : Léo Mangeolle
Relecture scientifique : Léa Lachaud
Relecture de forme : Tristan Guyomar
Temps de lecture : environ 13 minutes.
Thématique : Matière condensée (Physique)
Publication originale : Villain J., La structure des substances magnétiques. Journal of Physics and Chemistry of Solids, 1959. DOI : 10.1016/0022-3697(59)90231-8

De nombreuses technologies modernes comme les IRM, le stockage sur disque dur ou encore les hauts-parleurs utilisent des aimants. Aussi appelés cristaux magnétiques, ces matériaux présentent une très grande variété de structures internes, en réponse aux contraintes dictées par les interactions entre les aimantations de tous les atomes du cristal. Les règles du jeu sont assez simples : les aimantations de deux atomes voisins doivent former un angle le plus proche possible d’une consigne (généralement, être alignées ↑↑ ou anti-alignées ↑↓), dictée notamment par la nature chimique du cristal et par sa géométrie. Mais le jeu reste complexe : si l’aimantation d’un atome doit s’anti-aligner avec ↑,←,↓ et → en même temps, quelle orientation choisir ? Comment trouver une solution à l’amiable qui satisfasse tous les atomes du cristal ? C’est ce problème diplomatique complexe que Jacques Villain a cherché à résoudre en 1959, afin d’expliquer comment des solutions globales très diverses peuvent émerger à partir de quelques règles d’interaction locales simples.
Que cherche-t-on à résoudre au juste ?
Quand on joue avec un aimant, on sait juste que c’est un morceau de fer qui est globalement aimanté. Mais d’où provient cette aimantation à l’échelle microscopique ? Depuis la découverte de la structure quantique des atomes, on sait que chaque atome de l’aimant possède sa propre aimantation locale (on utilisera le terme impropre mais couramment utilisé spin dans la suite). L’aimantation globale du morceau de fer s’explique alors par le fait que tous les spins des atomes s’alignent dans une même direction. Mystère résolu. Mais clairement, tous les aimants ne sont pas en fer, et tous les métaux ne collent pas à la porte du frigo ! L’aluminium, par exemple, n’est pas naturellement aimanté.
En fait, dès le début du XXe siècle, des comportements très divers ont pu être identifiés, comme le ferromagnétisme (comme celui d’un aimant en fer, qui possède sa propre aimantation, permanente dans le temps) et le paramagnétisme (comme celui d’un morceau d’aluminium, qui n’a pas d’aimantation propre mais peut s’aimanter temporairement si on l’approche d’un aimant), mais aussi beaucoup d’autres, plus compliqués. À chaque comportement macroscopique correspond un agencement microscopique des spins, qu’en général on ne connaît pas. C’est cette structure microscopique que J. Villain cherche à prédire dans son article.
L’approche utilisée est de traiter les spins classiquement (c’est-à-dire sans utiliser la mécanique quantique), autrement dit, en assimilant le spin de chaque atome du cristal à un vecteur (de norme non fixée) pouvant pointer dans n’importe quelle direction. Cette approche classique, plus de trente ans après l’avènement de la description quantique des matériaux magnétiques, peut sembler cavalière. Il existe même des arguments théoriques qui garantissent qu’une solution classique ne peut pas être le véritable état fondamental des spins, mais seulement une approximation (qui peut être très bonne… ou très mauvaise, comme dans le cas de la chaîne de spins résolue par Hans Bethe, dont la solution exacte est tout sauf classique : [1]). Cependant, les observations expérimentales viennent justifier l’hypothèse classique : depuis 1951, la diffusion de neutrons a permis de sonder précisément les spins à l’échelle locale, mettant en évidence un état fondamental quasi-classique dans de très nombreux matériaux (par exemple l’antiferromagnétisme et le ferrimagnétisme décrits par Louis Néel). C’est pourquoi l’auteur choisit de décrire les spins classiquement.
Dans son article, J. Villain s’attaque simultanément à toute une variété d’interactions : non seulement des interactions entre plus proches voisins, mais aussi avec des voisins arbitrairement éloignés. La nature de ces interactions (alignantes, anti-alignantes, ou autres) dépend de nombreux paramètres, notamment la nature chimique des atomes impliqués, la géométrie précise du cristal (qui elle-même peut dépendre de la température, de la pression, etc.), la présence d’autres atomes à proximité, un éventuel champ magnétique extérieur, etc. Déterminer ces interactions est un sujet en soi, qui n’est pas celui de la publication — ce dernier s’attelle plutôt à déduire des comportements à grande échelle à partir de ces règles d’interaction microscopiques supposées connues. Ainsi, à basse température, c’est-à-dire lorsque l’agitation thermique ne vient pas perturber l’orientation des spins, ces interactions donnent lieu à diverses configurations possibles : quand les voisins immédiats tendent à aligner leurs spins, on s’attend à du ferromagnétisme (Figure 1a) ; quand ils tendent tendent à les anti-aligner, sur réseau carré on s’attend à de l’antiferromagnétisme (Figure 1b), mais pour un réseau triangulaire, à quoi s’attendre ? La Figure 1c montre qu’une solution antiferromagnétique n’est pas satisfaisante, car alors un tiers des spins ne sait pas sur quel pied danser : faut-il s’anti-aligner avec les bleus (au prix de devoir s’aligner avec les rouges), ou le contraire ? Ou ni l’un ni l’autre ? C’est notamment à cette question que l’article apporte une réponse.

L’approche de champ moyen
Pour résoudre ce problème de voisinage, l’article utilise une approche simplifiée dite de champ moyen. Si l’on considère un spin donné, cela consiste à considérer tous ses voisins non pas dans leurs détails individuels compliqués, mais seulement en moyenne, sous la forme d’un champ magnétique effectif, appelé champ moléculaire dans la publication. Cette approche, bien connue depuis 1907 (article de Weiss développant cette approche : [2]), permet de distinguer deux comportements distincts selon la température :
- À haute température, l’agitation thermique domine les interactions et on observe une phase désordonnée d’aimantation moyenne nulle en l’absence de champ magnétique extérieur, c’est-à-dire qu’à chaque instant il y a en moyenne autant de spins pointant dans une direction que dans la direction opposée, et tous les spins se retournent sans arrêt au gré des fluctuations thermiques. On est alors dans la phase dite paramagnétique : les spins n’ont pas réussi à s’accorder pour construire une aimantation globale, et le cristal n’a pas d’aimantation propre.
- À l’inverse, à basse température, ce sont les interactions entre les spins qui dominent, et on observe une phase ordonnée, figée dans le temps à l’abri des fluctuations thermiques. Dans cette phase dite ferromagnétique, le cristal peut avoir une aimantation propre, car les spins ont trouvé leur solution de compromis, dont la structure précise dépend bien sûr des règles d’interaction entre spins voisins.
La transition entre ces deux comportements radicalement différents (on parle de phases) se produit à une température particulière, dite température critique, que l’approche adoptée dans l’article permet de calculer, par une méthode très similaire au calcul de la température de Curie pour la transition ferromagnétisme-paramagnétisme effectué par Weiss en 1907. Par exemple, pour un aimant en fer, la température critique est de 770°C [*] : à température ambiante, on se trouve donc bien dans la phase ordonnée, et le fer présente une aimantation globale qui lui permet de coller à la porte du frigo.
On sait maintenant qu’il existe une phase ordonnée à basse température. La principale question à laquelle il reste à répondre est : à quoi ressemble cette phase ordonnée ? L’article donne la réponse : la solution globalement optimale adoptée par les spins est celle qui minimise l’énergie libre [**] d’interaction — schématiquement, il s’agit de minimiser le mécontentement général. On parle d’état fondamental de l’ensemble des spins. Le résultat principal de l’article est donc une formule générale qui donne la solution optimale pour tout système de spins, quelles que soient les règles d’interaction. On retrouve des résultats que l’on connaissait déjà, comme le ferromagnétisme ou l’antiferromagnétisme de Néel (voir Figure 1) ; mais la formule obtenue par J. Villain permet aussi, par exemple, d’obtenir la solution au problème de répulsion de plus proches voisins sur le réseau triangulaire : il s’agit de la solution dite 120 degrés (voir Figure 2).

On voit que la solution n’est pas unique : il peut y avoir plusieurs solutions, voire une infinité. Par exemple, pour la solution 120 degrés (Figure 2), tout ce qu’il faut savoir est que les flèches représentant deux spins voisins forment un angle de 120° entre elles ; mais en faisant tourner tous les spins simultanément d’un angle quelconque, on obtient encore une solution 120 degrés (ainsi la configuration (Figure 2b) est obtenue en tournant tous les spins de la configuration (Figure 2a) de 90 degrés dans le sens horaire — mais on aurait pu choisir 75 degrés, 187 degrés, etc.
Ce résultat est-il satisfaisant ?
La solution donnée par la publication pour la phase ordonnée est celle qui minimise globalement l’énergie libre, c’est-à-dire, schématiquement, qui minimise le mécontentement général : c’est une solution de compromis. On peut se demander si cette solution est localement stable, c’est-à-dire, répondre à la question : la structure magnétique pourrait-elle se désordonner spontanément si des spins rebelles décidaient d’améliorer leur sort individuel au détriment du bien-être général ? Cette question se pose notamment à cause de l’approche de champ moyen, qui est généralement trop optimiste sur l’existence de phases ordonnées ; on le sait par exemple dans le cas de la chaîne 1D de spins classiques, où une approche de champ moyen prédit une phase ordonnée qui, en réalité, est détruite par la prolifération de défauts (voir par exemple [3]). L’auteur choisit donc prudemment de vérifier que sa solution ne tombe pas à l’eau pour les mêmes raisons.
Et après vérification : tout va bien ! J. Villain prouve que sa solution globale garantit à chaque spin la meilleure configuration individuelle possible, c’est-à-dire l’orientation qui minimise son énergie libre d’interaction avec ses voisins, lorsque ceux-ci restent immobiles. Ainsi, même sous l’effet d’une fluctuation, aucun des spins n’a intérêt à bouger puisqu’il est déjà dans la configuration la plus stable qui soit pour lui. De plus, la stabilité de cette solution ordonnée globale ne dépend pas de la température : elle reste la solution optimale jusqu’à la température critique, comme cela est observé par exemple dans le cas du ferromagnétisme. En outre, on sait par l’expérience que de très nombreux cristaux magnétiques s’ordonnent effectivement à basse température : la solidité du résultat est donc en prime confirmée par l’expérience (du moins, dans de nombreux cas : il peut arriver que cette solution ordonnée soit déstabilisée non pas par l’agitation thermique, mais par des phénomènes dynamiques, comme les ondes de spin, ce qui se produit surtout dans des systèmes à 1D ou 2D).
Quelles structures peut-on espérer rencontrer ?
On sait donc que la solution obtenue dans l’article est une bonne solution stable, pour des règles d’interaction et une structure cristalline données. Ces deux données ne sont bien sûr pas indépendantes dans la réalité, même si on peut influer sur les règles d’interaction sans trop modifier la structure cristalline en remplaçant ponctuellement certains atomes par d’autres, aux propriétés magnétiques différentes (on parle de dopage) ; en revanche, dans les simulations numériques, tout devient possible ! On peut donc maintenant essayer d’anticiper les expériences : quelles structures magnétiques peuvent, a priori, apparaître si l’on explore différentes règles du jeu ?
Une première propriété générale qu’ont en commun toutes ces solutions : elles sont toujours planaires, c’est-à-dire que les vecteurs qui représentent les spins dans la phase ordonnée sont toujours situés dans un même plan. Par exemple, Figure 1 : tous les spins sont contenus dans le plan de la feuille ; mais on est en droit de les basculer hors du plan, pourvu qu’ils restent parallèles les uns aux autres (ce sera encore une solution ferromagnétique). A priori c’est un peu dommage, car cela contraint les structures autorisées par la théorie : il y a des états fondamentaux magnétiques que l’on ne verra semble-t-il jamais. Mais en fait, c’est plutôt une bonne nouvelle : si dans une expérience on rencontre un état fondamental qui n’est pas planaire, on sait immédiatement que le matériau ne vérifie pas les hypothèses et approximations postulées ici par J. Villain, et qu’il présente donc peut-être des propriétés très intéressantes !
Une autre propriété générale : la solution trouvée est toujours périodique, c’est-à-dire que le même motif de spins se répète indéfiniment dans le cristal. C’est évidemment le cas pour (Figure 1a) et (Figure 1b), mais aussi pour des solutions moins évidentes comme la solution 120 degrés. Là encore, c’est peut-être décevant car on n’a droit qu’aux structures périodiques. Mais cela cache à nouveau une bonne surprise puisque rien ne dit que les périodes du réseau cristallin et de la structure de spins doivent être reliées l’une à l’autre ! Si l’on ne se limite pas à des interactions entre plus proches voisins, mais que, comme J. Villain, on considère aussi des interactions avec des voisins plus éloignés, il est possible d’obtenir une structure magnétique incommensurable avec le réseau d’atomes. C’est-à-dire que si le cristal est périodique, la structure de spins l’est aussi, mais leurs périodes n’ont pas de diviseur commun si bien qu’il n’existe pas de période globale sous laquelle les deux réseaux sont périodiques en même temps. Un peu comme si l’on mettait côte-à-côte une horloge qui fonctionne et une horloge défaillante qui se décale progressivement : au cours du temps, l’angle entre leurs deux aiguilles prendra bien plus de valeurs différentes que si les deux horloges étaient parfaitement synchronisées, auquel cas cet angle serait toujours zéro. Cela pourrait apparaître comme un point de détail, mais c’est en fait un résultat très enthousiasmant, puisqu’il ouvre la porte à toute une variété de structures magnétiques nouvelles (et plutôt jolies, voir Figure 3), comme des structures hélicoïdales par exemple.

Quel intérêt aujourd’hui ?
Connaître le fondamental classique n’est évidemment pas la fin de l’histoire dans de nombreux matériaux qui affichent des propriétés beaucoup plus bizarres qu’une simple structure ordonnée. Mais c’est un premier outil qui peut être très utile, par exemple, pour l’étude des ondes de spin : si l’on veut étudier les petites oscillations des spins classiques autour de leur position d’équilibre, la moindre des choses est de connaître ladite position d’équilibre, et cet article apporte à ce problème une solution peut-être imparfaite, mais prête à l’emploi.
D’autre part, la recherche actuelle en physique de la matière condensée s’intéresse beaucoup aux cas où l’approche de la publication ne fonctionne pas du tout, ce qui peut arriver lorsque la dimension effective du matériau étudié n’est pas 3, mais plutôt 2 (des matériaux en couches) ou 1 (certains matériaux constitués de chaînes d’atomes parallèles). Dans ces cas-là, il n’est en général plus du tout judicieux d’appliquer la démarche de l’article, qui assimile les spins à des vecteurs interagissant classiquement. Il faut absolument tenir compte des phénomènes quantiques à l’œuvre pour expliquer les résultats expérimentaux.
[*] Wikipédia, Température de Curie.
[**] Définition d’énergie libre — précision de l’auteur : dans le cas d’interactions répulsives, l’énergie du système formé par deux spins alignés est élevée car il est coûteux énergétiquement de braver leur répulsion en les maintenant ainsi côte-à-côte. Ainsi, plus l’énergie d’une configuration est élevée, moins cette configuration est probable ; on s’attend donc à ce que, en moyenne, les spins se placent dans une configuration où l’énergie est minimale.
[1] Bethe, H., Zur Theorie der Metalle. Z. Physik, 1931. DOI : 10.1007/BF01341708. [Publication scientifique]
[2] Weiss P., L’hypothèse du champ moléculaire et la propriété ferromagnétique. J. Phys. Theor. Appl., 1907. DOI : 10.1051/jphystap:019070060066100. [Publication scientifique]
[3] B. Diu, C. Guthmann, D. Lederer, B. Roulet, « Physique Statistique », complément III.J p. 467. [Livre de science]