Cet article a été traduit depuis le site Softbites

Écriture (anglais) et traduction : Matthieu Martin
Relecture scientifique : Jérémy Ferrand
Relecture de forme : Eléonore Pérès

Difficulté :
Temps de lecture : environ 7 minutes.
Thématique : Matière molle (Physique)

Publication originale : Bricard A., Caussin J.-B., et al., Emergence of macroscopic directed motion in populations of motile colloids. Nature, 2013. DOI : 10.1038/nature12673. Accès libre sur HAL.

Avez-vous déjà vu ces grandes formes mouvantes se déplacer dans le ciel, faites de milliers d’étourneaux ? Ou les poissons nageant en larges bancs dans l’océan (comme illustré sur la Figure 1) ? C’est ce qu’on appelle des mouvements collectifs : la capacité de nombreuses entités individuelles à s’organiser et à se déplacer en groupes et sans leader. Ce phénomène a été observé à diverses échelles spatiales dans le monde vivant — des oiseaux aux sauterelles, en passant par les cellules et les bactéries. Même chez les humains, des mouvements collectifs apparaissent dans certaines situations, comme dans les mouvements de foule (dans les fosses de concerts par exemple). Les physiciens se sont penchés sur ce phénomène au cours des dernières décennies en essayant de répondre à plusieurs questions : comment des organismes différents peuvent-ils avoir le même comportement ? Quelles sont les caractéristiques communes à tous ces organismes qui leur permettent de se déplacer d’une manière aussi synchronisée ?

La clé de l’émergence d’un mouvement collectif est l’interaction, c’est-à-dire la capacité des individus à modifier leur comportement pour coordonner leurs mouvements avec ceux de leurs voisins. Les détails et la forme de ces interactions sont difficiles à modéliser et à contrôler dans de nombreux systèmes vivants, ou créés par l’humain. Parfois, la nature de ces interactions est même encore inconnue. Dans l’article discuté ici, Antoine Bricard, Jean-Baptiste Caussin et leurs collaborateurs ont montré comment un mouvement collectif pouvait naître à partir d’interactions physiques bien identifiées.

L’un des premiers physiciens à s’être intéressé à ces questions a été Tamas Vicsek dans les années 90 [1]. Il a montré, à l’aide de simulations numériques, que le mouvement collectif peut émerger de règles simples (comme l’alignement des vitesses). Bien que de nombreuses études théoriques et numériques aient suivi, seules quelques expériences ont été réalisées. En effet, en physique expérimentale, le contrôle et la reproductibilité d’un système sont essentiels pour permettre son étude.

Élever des milliers d’oiseaux dans un laboratoire n’est peut-être pas la façon la plus pratique d’étudier le phénomène, et des systèmes biologiques encore plus simples, comme les bactéries, ont également leurs propres contraintes et n’ont pas exactement le même comportement. Pour s’affranchir de ces problèmes liés à la nature biologique de l’objet d’étude, certains chercheurs ont préféré construire leur propre système artificiel. C’est la démarche adoptée par l’équipe de recherche, au Laboratoire de Physique et Chimie des milieux hétérogènes de l’ESPCI Paris et au Laboratoire de Physique de l’École Normale Supérieure de Lyon. Pour étudier le mouvement collectif, ils ont construit un système artificiel composé de millions de minuscules billes de plastique (de 5 μm de diamètre) capables de se déplacer librement, d’interagir avec leurs voisins et surtout de s’organiser en groupe.

Pour mettre en mouvement ces billes inertes, les chercheurs ont utilisé un phénomène appelé l’électro-rotation de Quincke. L’idée est de convertir de l’énergie électrostatique en énergie de rotation mécanique. Ici, la rotation est provoquée par un champ électrique constant, E₀, appliqué à des billes isolantes (elles ne permettent pas au courant de passer) immergées dans un liquide conducteur (comme de l’eau salée, qui permet au courant de passer). Les billes se polarisent alors sous l’effet du champ électrique. Puis, de petites fluctuations dans la répartition des charges électriques font basculer l’orientation de la bille. Toujours sous l’action du champ électrique, cette perturbation s’amplifie, entraînant la rotation de la bille. Elle commence alors à rouler sur le fond de la cuve et accélère jusqu’à atteindre une vitesse constante.

Les chercheurs appellent ces billes activées des rollers (littéralement des rouleurs). Ils se déplacent à la même vitesse v, pilotée par le champ E₀. Comme on peut le voir sur la Figure 2, les billes se déplacent individuellement dans n’importe quelle direction et il n’y a donc pas de mouvement global dans une seule et unique direction. Alors comment ce système désordonné peut-il basculer vers un système ordonné ?

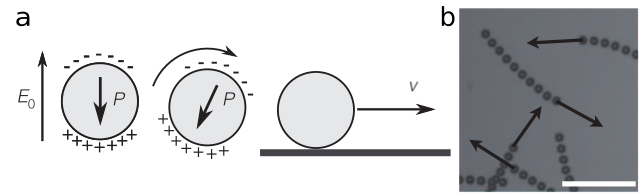
Comme l’électro-rotation de Quincke est un phénomène physique connu, l’équipe de recherche a pu mieux décrire mathématiquement les interactions entre les rollers. Tout d’abord, les billes interagissent par interaction électrostatique (comme les cheveux qui se dressent lorsqu’on enlève un pull), une force qui dépend de la distance entre les billes. Deuxièmement, les billes interagissent de manière hydrodynamique car lorsqu’une bille se déplace dans un liquide, un écoulement de fluide est généré autour d’elle. Cela entraîne un courant auquel les rollers autour vont être sensibles. Un peu comme un nageur qui ressent les vagues produites par un autre nageur à proximité de lui. De plus, la théorie montre que la combinaison de ces deux interactions physiques tend à aligner les vitesses des rollers au sein d’un groupe. Lorsque deux billes sont assez proches l’une de l’autre, elles changent légèrement de direction pour rouler dans la même orientation. Avec le temps, elles finissent toutes par se déplacer dans le même sens.

Pour étudier des billes microscopiques sur des longueurs plusieurs fois supérieures à leur taille, les chercheurs ont choisi de les placer dans une zone en forme de piste de course (Figure 3a). Les rollers s’organisent alors spontanément et une grande bande composée de millions de ces billes se déplacent autour de la piste. Bien sûr, les rollers doivent être assez proches pour que les interactions soient efficaces. Les Figures 3b-d montrent comment les rollers changent de comportement au fur et à mesure qu’ils deviennent plus resserrés (c’est-à-dire que leur densité augmente). Dans la Figure 3b, les rollers semblent errer dans des directions aléatoires parce qu’ils sont trop éloignés les uns des autres pour interagir, alors que dans la Figure 3d, les rollers, à haute densité, se déplacent tous globalement dans le même sens. Et à mesure que d’autres rollers sont ajoutés dans la même zone, les interactions entre eux deviennent plus efficaces.

Cette transition d’un état désordonné à un état ordonné est appelée une transition de phase. Dans la plupart des cas familiers, par exemple les transitions de phase entre l’eau et la glace, celle-ci dépend de la température. Ici, la densité joue le rôle de paramètre de contrôle, ce qui signifie que l’équipe de recherche a étudié la densité minimale requise pour qu’un mouvement collectif émerge. En associant cette observation expérimentale à une description théorique des interactions, l’ingrédient clé à la base du système, l’équipe est allée plus loin que quiconque à l’époque dans la description de ces phénomènes.

Le mouvement collectif semble naturel chez de nombreux organismes vivants, mais il est encore mal compris par les scientifiques. Cette publication souligne l’importance des interactions entre les individus d’un groupe au cours du processus de mouvement collectif. Bien que cette étude soit spécifique et ne tienne pas compte des mécanismes à l’œuvre dans la plupart des systèmes biologiques, elle constitue un grand pas vers la compréhension de ce phénomène. La comparaison de ces résultats avec les études de biologistes, d’éthologues et de mathématiciens m’amène à me demander la chose suivante : imaginons qu’un scientifique travaillant dans son laboratoire soit comme un marcheur aléatoire, alors, quelle belle image émergera du travail de centaines de scientifiques en interaction les uns avec les autres pour comprendre le mouvement collectif ?

---

[1] Vicsek T., et al., Novel Type of Phase Transition in a System of Self-Driven Particles, Physical Review Letters, 1995. DOI : 10.1103/PhysRevLett.75.1226. [Publication scientifique]

---