Effet photovoltaïque : du nouveau sous le Soleil

Chargement de l'article...

Écriture : Gaëlle Vitali-Derrien
Relecture scientifique : Grégory Gredat et Charles Paillard
Relecture de forme : Eléonore Pérès et Camille Petitfils

Temps de lecture : environ 15 minutes.
Thématiques : Matière condensée et Photonique (Physique)

Publication originale : Spanier J. E., et al., Power conversion efficiency exceeding the Shockley–Queisser limit in a ferroelectric insulator. Nature Photonics, 2016. DOI : 10.1038/nphoton.2016.143

Photographie de panneau solaire en gros plan, sur laquelle est écrit le mot "dépassé" en majuscules.

La récupération d’énergie est un enjeu majeur du XXI^e siècle, et nous avons tous croisé au moins une fois les fameux panneaux solaires bleus qui permettent de convertir la lumière du Soleil en électricité. Mais ces panneaux sont soumis à un destin tragique… En effet, ils n’atteignent même pas les 50 % d’efficacité ! C’est alors qu’un nouvel effet surprenant fait son apparition : l’effet photovoltaïque anormal, dont l’origine physique même s’affranchit de cette limitation.

La transition vers des énergies renouvelables, telles que l’éolien ou le solaire, ainsi que la limitation de l’utilisation des énergies fossiles, sont des problématiques cruciales pour notre société. Alors, qu’est-ce qu’on attend ? Pourquoi est-ce si difficile de remplacer le pétrole ? La réponse tient en un mot : le rendement. Tout l’enjeu est de transformer une source d’énergie en électricité utilisable ; on parle alors de conversion. Le rendement est la part d’énergie qui est transformée en électricité, c’est donc une donnée primordiale ! Malheureusement, aucune conversion n’atteint un rendement de 100 %. Loin de là même… Pour la conversion d’énergie solaire, aussi appelé effet photovoltaïque, il est d’ailleurs limité à environ 20 % dans les panneaux solaires courants ! À titre de comparaison, parmi les énergies renouvelables, une éolienne a un rendement d’environ 35 % tandis que les énergies fossiles ont des rendements bien meilleurs, la transformation du pétrole en carburant atteignant par exemple les 80 % [1]. Malheureusement pour l’effet photovoltaïque, optimiser les dispositifs ou les matériaux ne permettra pas d’atteindre de tels rendements : il est intrinsèquement limité, à environ 30 %, contraint par les lois de la physique ! Mais alors, sommes-nous condamnés à ne pouvoir tirer qu’un tiers de l’énergie du Soleil ? Ne vous en faites pas ! Bien que l’effet photovoltaïque de nos panneaux solaires ait ses limites, il existe un nouveau phénomène plus efficace, qui fait du bruit dans les labos de physique et dans la publication de J. E. Spanier et son équipe : c’est l’effet photovoltaïque anormal.

De la lumière à l’électricité, il n’y a qu’une particule… ou deux

Il est temps de comprendre ce qui se passe dans ces fameux panneaux solaires. C’est en étudiant le fonctionnement de l’effet photovoltaïque que nous allons comprendre d’où vient la limitation de rendement de conversion. Alors, quel est le secret des panneaux solaires pour convertir la lumière du Soleil en électricité ?

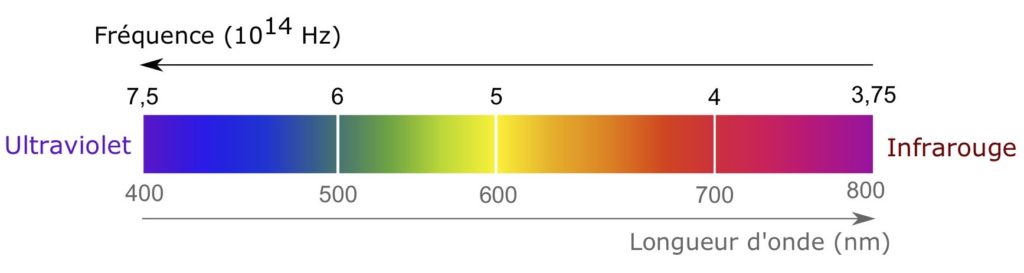
Dans un premier temps, intéressons-nous à l’énergie qui nous vient du Soleil. Cette énergie nous arrive sous forme de lumière, divisée en unités insécables que l’on appelle photons. Ces photons ont chacun une énergie bien spécifique qui dépend de leur couleur. Bien que la lumière du Soleil nous paraisse blanche, elle est en fait composée d’une infinité de couleurs différentes (on les voit notamment sur les arcs-en-ciel). Les couleurs tendant vers le bleu correspondent à des photons plus énergétiques, et celles tendant vers le rouge à des photons qui le sont moins [*] (Figure 1).

Schéma composé d'une bande avec un dégradé de couleurs allant du violet , situé à gauche, au rouge rubis, situé à droite en passant par le vert, le jaune et le orange. À gauche du violet il est écrit "Ultraviolet" et à droite du rouge "Infrarouge". Une flèche en dessous de la bande va de la gauche vers la droite et indique "longueur d'onde (nanomètres)". Une autre flèche, au dessus de la bande, va de la droite vers la gauche et indique "fréquence (10 puissance 14 hertz)". Pour certaines couleurs, la longueur d'onde et la fréquence sont indiquées : violet 400 nanomètres et 7,5 fois 10 puissance 14 hertz ; vert 500 nanomètres et 6 fois 10 puissance 14 hertz ; jaune 600 nm et 5 fois 10 puissance 14 hertz ; orange foncé 700 nanomètres et 4 fois 10 puissance 14 hertz ; rouge rubis 800 nanomètres et 3,75 fois 10 puissance 14 hertz. — **Figure 1**. **La lumière que nous recevons du Soleil est composée de petites unités, les photons, chacun possédant une énergie qui lui est propre et qui dépend de sa fréquence/de sa couleur**. À chaque fréquence correspond une longueur d’onde (la fréquence diminue quand la longueur d’onde augmente). Les fréquences du spectre visible s’étendent de 3,75 à 7,5 x 10¹⁴ Hz, et les longueurs d’onde de 400 à 800 nm (1 nm = 10^-9 m).

Les photons sont absorbés par les panneaux solaires et vont transmettre leur énergie : c’est comme cela que l’on en tire de l’électricité. Mais au fait, savez-vous ce qu’est réellement l’électricité et d’où elle vient ? L’électricité est, elle aussi, composée d’unités insécables mais cette fois-ci ce sont des électrons : des particules qui ont une charge électrique négative. Ils sont présents partout dans la matière car ils font partie des atomes. Ce qui est intéressant, c’est que les électrons se mettent en mouvement dans la matière. Il y a alors transport de charge : c’est par définition de l’électricité ! L’effet photovoltaïque, c’est donc la conversion de photons en électrons en mouvement. Mais alors, comment est-ce que ça se passe ?

La conversion lumière-électricité se fait à l’intérieur du matériau du panneau solaire. Cependant, bien que tous les matériaux possèdent des électrons, ils ne sont pas tous sujets à l’effet photovoltaïque. Pour qu’ils le soient, il faut que leurs électrons se mettent à conduire l’électricité après avoir reçu l’énergie du photon. L’énergie de l’électron va donc être une propriété centrale !

Des électrons en bande organisée

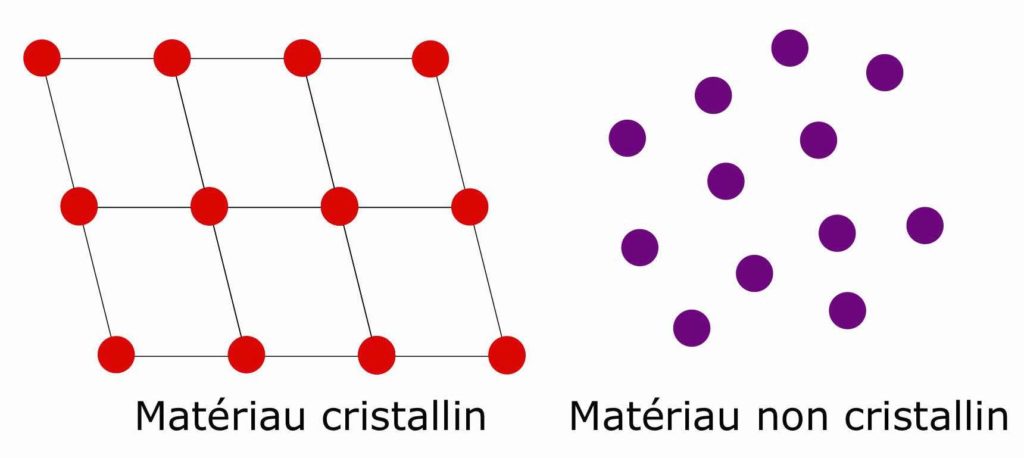
Dans les panneaux photovoltaïques, les matériaux sont des cristaux, comme les pierres précieuses des bijoux ! Et ils partagent avec eux une propriété intéressante : leurs atomes sont arrangés de manière géométrique et répétée, comme sur la Figure 2.

Schéma en deux parties. À gauche, des points, régulièrement espacés et alignés, forment un quadrillage. Il est légendé "Matériau cristallin". À droite, des points sont placés de manière aléatoire. Il est écrit "Matériau non cristallin". — **Figure 2**. Matériau cristallin **à gauche** et matériau non cristallin (ou amorphe) **à droite**. Les points représentent des atomes.

Lorsqu’un matériau a une structure cristalline, l’énergie de ses électrons est impactée (voir la version Approfondissement pour en savoir plus) ! Cette énergie se répartit sous forme de bandes bien définies. Chaque bande peut accueillir un nombre fini (= déterminé) d’électrons et lorsqu’une bande est remplie, les électrons vont peupler la suivante. Les bandes d’énergie grandissante se remplissent ainsi les unes après les autres (Figure 3). Avant de nous lancer à la poursuite des électrons, il convient de poser quelques mots de vocabulaire. La dernière bande complètement remplie, c’est-à-dire celle de plus haute énergie, est appelée bande de valence (Figure 3, bande n°1). Lorsqu’il y a suffisamment d’électrons pour commencer à remplir la suivante, cette dernière est appelée bande de conduction (Figure 3, bande n°2). Vous l’avez peut-être deviné, mais c’est dans la bande de conduction que les électrons vont pouvoir conduire l’électricité ! Cependant, la conduction n’est pas possible si cette bande est complètement remplie. À ce moment-là, elle deviendrait alors une bande de valence par définition, et la bande de conduction serait vide. Pour vous le représenter, vous pouvez imaginer les bandes peuplées d’électrons comme des bouteilles d’eau plus ou moins pleines. Si la bouteille est complètement remplie ou complètement vide, on aura beau la secouer, il n’y aura pas beaucoup de mouvement… alors que si celle-ci n’est qu’à moitié pleine, on verra bien l’eau bouger ! Les matériaux ayant leur bande de conduction vide sont dits isolants, par opposition aux métaux dont la bande de conduction n’est que partiellement remplie. La zone entre les bandes de valence et de conduction est appelée bande interdite.

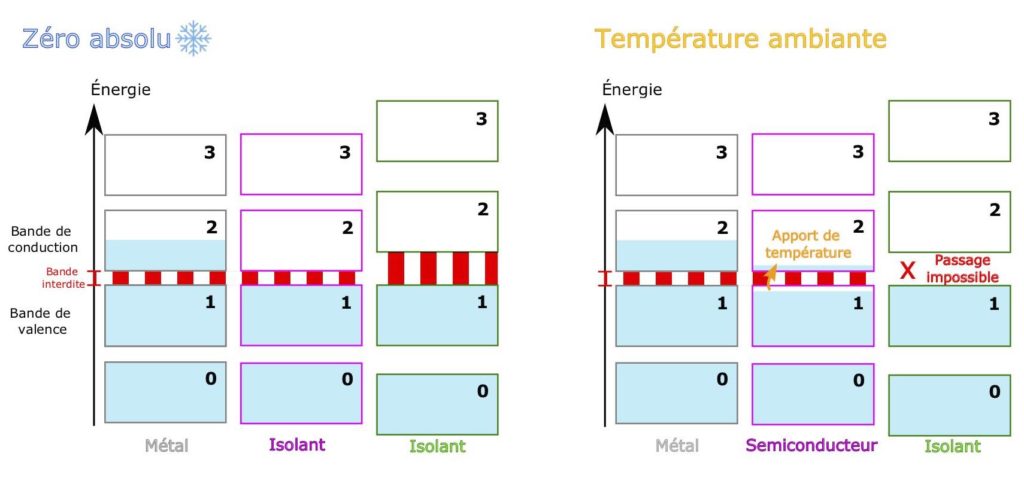
Schéma représentant les bandes électroniques. Elles sont représentées pour chaque matériau par des rectangles, placés les uns au-dessus des autres et numérotés de 0 à 3 (le 0 étant en bas et le 3 en haut). Une flèche allant de haut en bas indique le sens d'énergie croissante. La bande 1 est notée « bande de valence », la bande 2 « bande de conduction ». L’espace entre ces bandes est hachuré en rouge et est légendé « bande interdite ». La partie de gauche du schéma correspond au zéro absolu. Le premier matériau est noté « métal », en gris. Les rectangles 0 et 1 sont remplis de bleu, le rectangle 2 est rempli de bleu seulement à moitié. Le 3ème est vide. Le deuxième matériau est noté « isolant », en violet. Les rectangles 0 et 1 sont remplis de bleu, les 2 et 3 sont vides. Le troisième matériau est noté « isolant », en vert. Les rectangles 0 et 1 sont remplis de bleu, les 2 et 3 sont vides. L’espace entre les rectangles 1 et 2 est plus grand que pour les deux autres matériaux. La partie de droite correspond à la température ambiante. Le premier matériau est noté « métal », en gris. Les rectangles 0 et 1 sont remplis de bleu, le rectangle 2 est rempli de bleu seulement à moitié. Le 3ème est vide. Le deuxième matériau est noté « semiconducteur », en violet. Le rectangle 0 est rempli de bleu, le rectangle 1 est presque rempli (il reste une très fine partie blanche en haut du rectangle) et le rectangle 2 est un tout petit peu rempli. Le rectangle 3 est vide. Une flèche jaune part de la partie vide du rectangle 1 et va vers la partie remplie du rectangle 2, elle indique « apport de température ». Le troisième matériau est noté « isolant » en vert. Les rectangles 0 et 1 sont remplis de bleu, les 2 et 3 sont vides. Il y a une croix rouge dans l’espace entre les rectangles 1 et 2, et il est écrit « passage impossible ». — **Figure 3**. **Schéma des bandes électroniques pour différents matériaux, au zéro absolu et à température ambiante.** Les électrons (remplissage bleu) sont répartis en bandes (rectangles numérotés). La bande de valence (BV) est la dernière bande complètement remplie, notée « 1 » ; la bande de conduction (BC) est la suivante notée « 2 ». Celle-ci est à moitié pleine pour un métal, et vide pour un isolant. Ces deux bandes sont séparées par la bande interdite (hachures rouge et blanc). **À gauche**, la répartition au zéro absolu ; **à droite**, la répartition à température ambiante. Un semiconducteur (rectangles roses) est un isolant au zéro absolu. Grâce à l’apport d’énergie de la température, une partie des électrons de la BV (bande n°1) peut peupler la BC (bande n°2). Ceci n’est pas possible pour un isolant (rectangles verts).

Ces structures d’énergie en « bandes » ne sont pas immuables. En effet, un électron peut passer d’une bande à l’autre si son énergie augmente. C’est par exemple le cas quand il y a un apport de température ou… de photons ! Pour certains matériaux isolants, la température ambiante suffit à elle seule à faire passer quelques électrons de la bande de valence vers la bande de conduction. Ce sont ces matériaux qui vont nous intéresser, on les appelle les semiconducteurs [**].

Maintenant que les bandes électroniques n’ont plus de secrets pour vous, attaquons-nous au cœur du problème. Dans les semiconducteurs, la bande interdite n’est pas très haute (Figure 3, température ambiante, colonne du milieu). En d’autres termes, il est facile pour un électron de la passer et de finir dans la bande de conduction (bande n°2). C’est d’ailleurs si facile qu’il suffit d’un photon pour y parvenir… Mais attention, pas n’importe quel photon ! J’ai expliqué plus haut que les photons ont des énergies différentes en fonction de leur couleur. Pour faire passer un électron dans la bande de conduction, il faut que cette énergie soit supérieure à l’énergie de la bande interdite ! On s’attend alors à ne pouvoir utiliser que les photons très énergétiques envoyés par le Soleil… mais ce n’est pas complètement le cas. Si l’énergie du photon est très supérieure, cela va certes permettre d’avoir un électron de plus haute énergie, mais il n’y en aura toujours qu’un seul ; l’électron va d’ailleurs atteindre l’intérieur de la bande de conduction, mais il redescend ensuite jusqu’au minimum de celle-ci (Figure 3, température ambiante, colonne du milieu, le rectangle rose n°2 est rempli depuis le bas). En effet, les électrons cherchent toujours à minimiser leur énergie à l’intérieur de leur bande. Finalement, pour chaque photon, on a soit la transmission d’un électron vers la bande de conduction, soit rien du tout. Les photons d’énergie inférieure à la bande interdite ne sont pas utilisés, et ceux qui la surpassent voient leur surplus perdu. Ce mécanisme est représenté sur la Figure 4. On parle de limite « Schockley-Queisser », elle détermine l’énergie qu’un matériau peut convertir par effet photovoltaïque et dépend de la bande interdite du matériau.

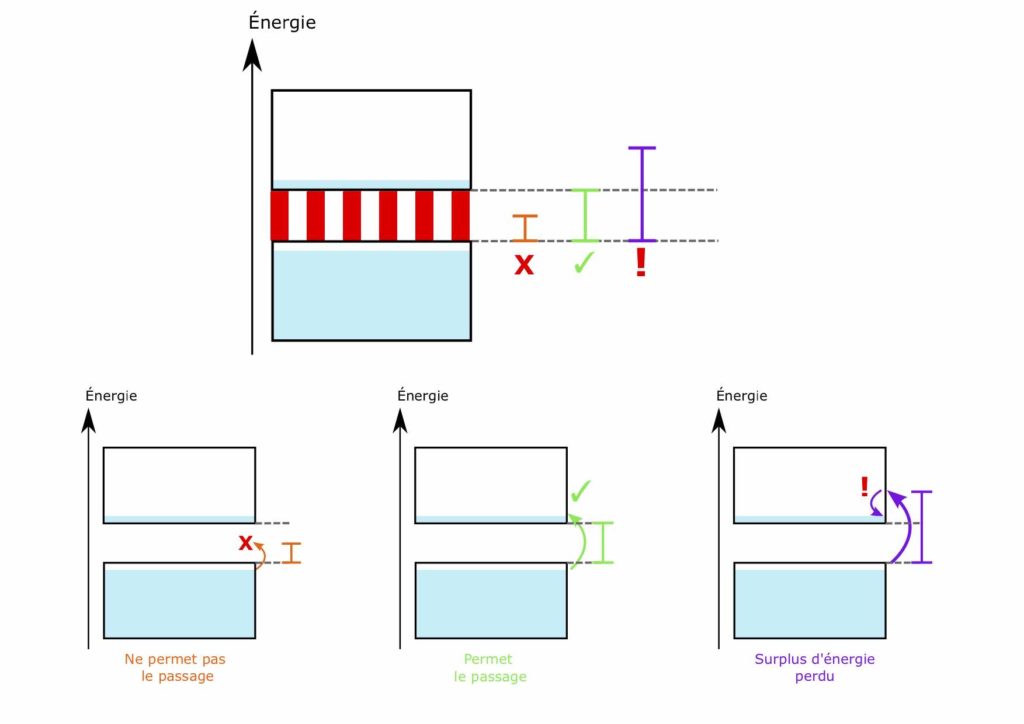
Schéma en deux parties. En haut, deux rectangles similaires à ceux du semiconducteur de la Figure 3 : celui du dessous est presque rempli de bleu et celui du dessus l’est un peu en bas. Entre ces deux rectangles, l’espace est hachuré en rouge et blanc. La hauteur de cet espace est marquée par deux lignes de pointillés qui continuent vers la droite. Trois segments verticaux de tailles différentes sont dessinés à côté. Le premier segment est orange et est plus petit que la hauteur de l'espace hachuré délimité par les pointillés. Sous cette barre il y a une petite croix rouge. Le deuxième segment est vert et sa taille fait exactement l’espace entre les deux lignes en pointillés. Sous cette barre, une coche verte. Le troisième est violet et sa taille dépasse l’espace entre les deux lignes en pointillés. Sous cette barre, un point d’exclamation rouge. À gauche, une flèche allant de haut en bas indique le sens des énergies croissantes. En bas, les deux rectangles remplis comme ci-dessus, la flèche et les pointillés sont répétés trois fois : à gauche, au milieu et à droite. Sur le schéma de gauche, il y a le petit segment orange vertical sur les pointillés du bas, et une petite flèche allant de l’espace vide du rectangle du bas à l’espace entre les deux rectangles, avec une croix rouge à côté de la flèche. Il est écrit en dessous « ne permet pas le passage ». Sur le schéma du milieu, il y a le segment vert entre les pointillés. Une flèche verte va de l’espace vide du rectangle du bas vers l’espace bleu du rectangle du haut, avec une coche à côté de la flèche. Il est écrit en dessous « permet le passage ». Sur le schéma de droite, il y a le grand segment violet qui dépasse des pointillés. Une flèche violette va de l’espace vide du rectangle du bas vers le milieu du rectangle du haut. Une deuxième flèche violette en part et redescend vers la partie remplie du rectangle du haut. A côté de cette dernière, on voit un point d’exclamation rouge. Il est écrit en dessous « surplus d’énergie perdu ». — **Figure 4. Apport énergétique de photons de différentes couleurs sur les électrons d’un semiconducteur**. Le formalisme est celui de la Figure 3. Les photons de différentes énergies sont représentés par les barres verticales de différentes hauteurs, la couleur du photon correspondant à son énergie. Le photon de petite barre orange est moins énergétique que le photon de moyenne barre verte qui est moins énergétique que le photon de grande barre violette. En fonction de leur énergie, les photons permettent ou non le passage d’électrons dans la bande de conduction : croix rouge = pas de passage ; check vert = passage. Les photons trop énergétiques voient leur surplus d’énergie dissipé (point d’exclamation violet).

Si on calcule la limite « Schockley-Queisser » pour le silicium (le matériau semiconducteur ayant la bande interdite permettant d’absorber un maximum de photons du Soleil) on arrive environ à 33 %… et c’est le meilleur des cas possibles ! C’est pour cela que même avec les matériaux les plus performants du marché, on n’atteint pas de grands rendements de conversion. Ça serait tout de même drôlement pratique s’il existait un moyen de ne pas perdre le surplus d’énergie des photons incidents…

(par)Anormal activity

Deux points limitent l’effet photovoltaïque classique : la bande interdite qui empêche d’utiliser les photons de plus faible énergie (Figure 3), et le surplus d’énergie des photons qui est perdu (Figure 4). La bande interdite est une caractéristique intrinsèque du matériau, alors il paraît difficile de la changer sans modifier complètement la composition du cristal. Mais pour le surplus d’énergie, c’est une autre histoire… Il existe un phénomène physique bien pratique qui permet de ne pas le perdre : c’est l’effet photovoltaïque anormal ! Ce dernier repose essentiellement sur une propriété : la structure cristalline du matériau [***].

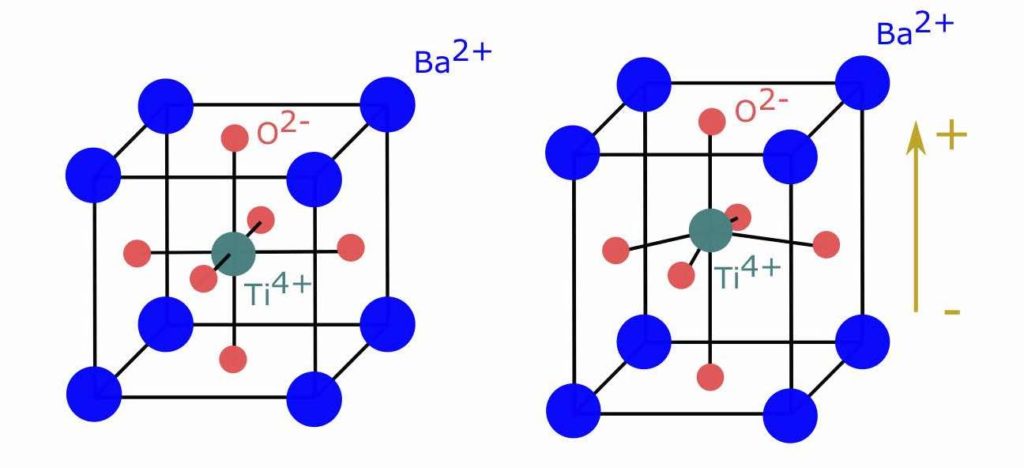
Nous avons vu plus haut que les matériaux composants les panneaux solaires sont des cristaux, leurs atomes ont une structure géométrique qui se répète. Cette structure montre des propriétés intéressantes quand elle perd en symétrie. Cela peut paraître indirect, mais c’est en fait très intuitif ! Il suffit de réfléchir aux implications que peut avoir une « perte de symétrie » : si la structure n’est pas symétrique, c’est que toutes ses directions ne sont pas équivalentes, comme sur la Figure 5 où la verticale est plus étirée que l’horizontale.

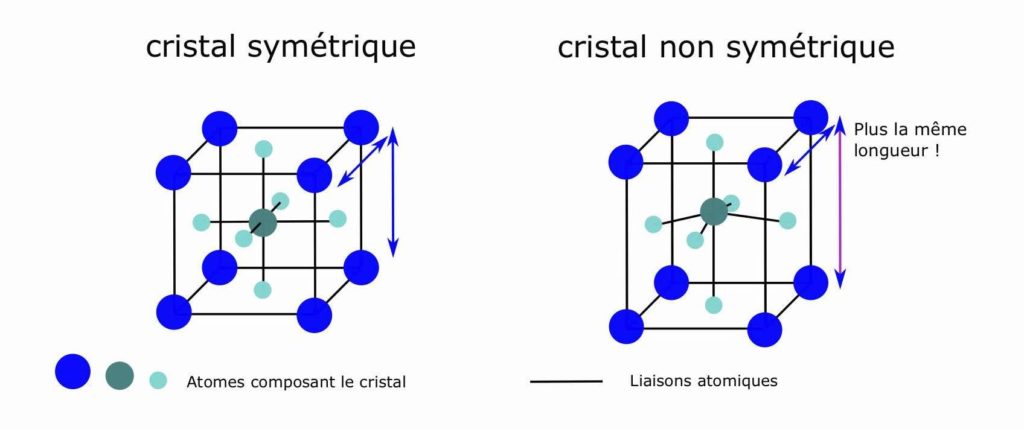
Schéma en deux parties. À gauche, il est écrit « cristal symétrique » et on voit un cube en perspective : de gros points bleus sont sur les sommets, de petits points cyan sont au milieu des faces, un point de taille moyenne vert est au milieu du cube. Les points cyan sont reliés au point vert. Deux flèches bleues indiquent que les arêtes verticales horizontales ont toutes la même longueur. À droite, il est écrit « cristal non symétrique » et on voit le même « cube » mais étiré en hauteur, c'est donc devenu un parallélépipède rectangle. Sur le côté, une flèche longe une des arêtes qui a été étirée, et une autre flèche une arête de taille inchangée. En dessous, une légende indique que les points sont les atomes composant le cristal, et les traits qui les relient sont des liaisons atomiques. — **Figure 5. Illustration de la différence de directionalité entre un cristal symétrique (gauche) et non symétrique (droite).** On observe à droite que le cristal est plus haut que large.

Le placement des atomes donne lieu à une ou plusieurs directions privilégiées. En effet, les atomes interagissent avec les électrons et ces interactions changent en fonction de l’énergie de ces derniers. Les électrons sont, par défaut, liés aux atomes (c’est le cas dans la bande de valence et celles du dessous, Figure 3, bandes n°0 et 1). Cependant, lorsqu’ils ont une énergie suffisante, ils peuvent s’affranchir de leurs interactions et se déplacer (ceci est possible lorsqu’ils se trouvent dans la bande de conduction, Figure 3, bande n°2). On peut se représenter les électrons comme des satellites ou des fusées : il y a les satellites en orbite qui restent près de la Terre et les fusées qui s’affranchissent de l’attraction terrestre et partent loin dans l’espace. Les interactions sont représentées par les murs et les flèches de la Figure 6.

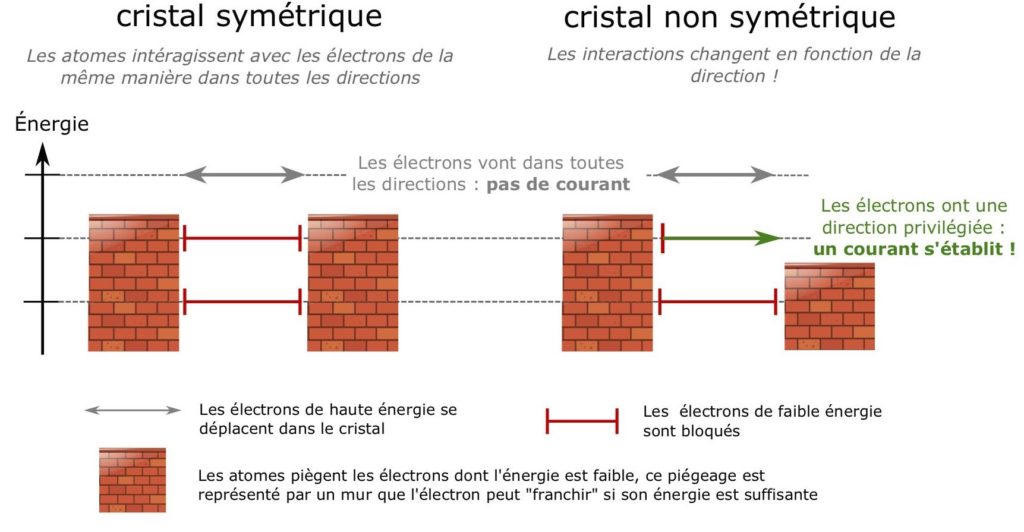
Schéma en deux parties. À gauche il est écrit « cristal symétrique, les atomes interagissent avec les électrons de la même manière dans toutes les directions » et à droite « cristal non symétrique, les interactions changent en fonction de la direction ! ». Tout à gauche du schéma, une flèche allant de haut en bas indique le sens des énergies croissantes. Trois positions sont marquées sur cette flèche : en bas, au milieu et en haut ; elles sont marquées par des lignes horizontales en pointillés qui s’étendent sur tout le schéma. Sous la figure, une légende indique que les flèches grises représentent les électrons de haute énergie qui se déplacent dans le cristal ; les barres horizontales rouges représentent les électrons de basse énergie qui sont bloqués ; les murs représentent les atomes qui piègent les électrons de basse énergie. À gauche, il y a deux murs qui vont du bas du schéma jusqu’entre les pointillés du milieu et du haut. Entre ces murs, des barres horizontales rouges recouvrent les lignes en pointillés du bas et du milieu. Une double-flèche grise recouvre la ligne en pointillés du haut, il est écrit en gris « les électrons vont dans toutes les directions, pas de courant ». À droite, il y a un mur allant du bas du schéma jusqu’entre les pointillés du milieu et du haut et à côté un autre mur, plus bas, dont la hauteur s'arrête entre les pointillés du bas et du milieu. Entre ces deux murs, une barre horizontale rouge recouvre la ligne en pointillés du bas. Une flèche verte recouvre la ligne en pointillés du milieu, et va du côté du grand mur jusqu’à celui du petit. Il est écrit en vert « les électrons ont une direction privilégiée, un courant s’établit ! ». Une double-flèche grise recouvre la ligne en pointillés du haut. — **Figure 6. Le déplacement possible des électrons à l’intérieur du cristal, selon la symétrie.** L’interaction des électrons avec les atomes est représentée par des murs et le déplacement des électrons par des flèches ou des segments. L’échelle des énergies est à gauche : les murs et les flèches qui sont plus hauts ont une énergie plus grande. Les murs emprisonnent donc les électrons de basse énergie et laissent passer ceux de haute énergie. Dans le cas symétrique (à **gauche**), les électrons de basse énergie sont bloqués près des atomes (segments rouges) et ceux de haute énergie sont propagés dans toutes les directions (double flèche grise). Dans le cas non symétrique (**à droite**), il y a des énergies pour lesquelles les électrons ne se propagent que dans une seule direction (simple flèche rouge et verte) et là, on a un courant électrique ! Crédit : image du mur tirée de Freepik/fond vecteur créé par brgfx.

Dans un cristal symétrique, les électrons énergétiques se propagent dans toutes les directions, il n’y a en moyenne pas de courant (Figure 6, à gauche). Cependant, dans un cristal non symétrique, la directionnalité permet aux électrons de haute énergie de se déplacer dans certaines directions uniquement, ce qui crée un courant électrique (Figure 6, à droite).

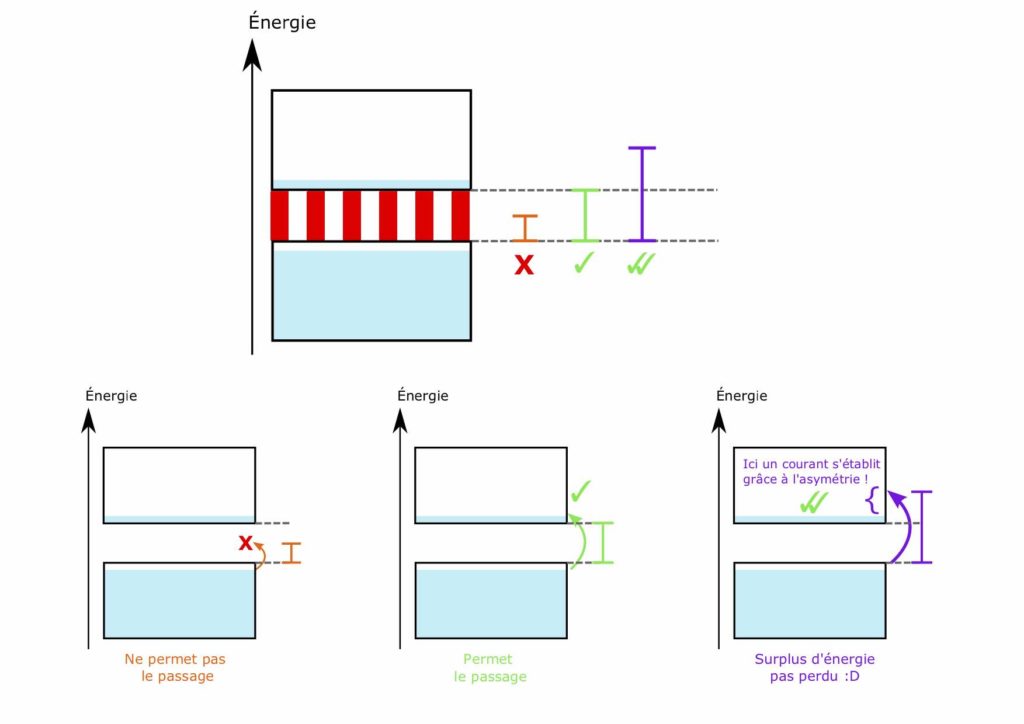
Ce qui est important, c’est que le courant électrique lié à l’asymétrie s’établit avant que les électrons atteignent le bas de la bande de conduction (Figure 4, droite, photon violet avec le point d’exclamation). Le surplus d’énergie des photons n’est alors pas perdu, et le rendement est augmenté (Figure 7) ! Grâce à l’effet anormal, on peut convertir efficacement les photons de haute énergie en électricité. Si durant leur transport, les électrons atteignent le bas de la bande de conduction, on repasse à l’effet photovoltaïque normal. L’effet anormal s’ajoute donc à l’effet normal, ce qui augmente le rendement !

Identique à la Figure 4, seules les parties avec la barre violette changent. Partie du haut : le symbole sous la barre violette est maintenant une double coche verte. En bas, une flèche violette va de l’espace vide du rectangle du bas vers le milieu du rectangle du haut. Il y a une accolade sur la zone entre le bout de la flèche violette et le haut de la partie remplie en bleu du rectangle. Il est écrit en violet « ici un courant s’établit grâce à l’asymétrie ! », avec une double coche verte. Il est écrit en dessous en violet « surplus d’énergie pas perdu :D » — **Figure 7.** Rappel et modification de la Figure 4 pour l’effet photovoltaïque anormal.

Dans le cas précis où le cristal n’est pas symétrique, et où l’asymétrie porte aussi sur les charges, on a bien une direction privilégiée pour les phénomènes électriques [****]. On parle alors de matériaux ferroélectriques (Figure 8). Tous les matériaux de cette famille sont soumis à l’effet anormal, ce qui leur donne un grand intérêt pour les chercheur·ses !

Similaire à la Figure 5, mais les points sur les faces des cubes sont ici rouges. Près des points bleus, aux sommets des cubes, est écrit « Ba2+ » ; près des points rouges sur les faces est écrit « O2- » ; près du point vert au centre est écrit « Ti4+ ». Le long de l’arête étirée du « cube » de droite, il y a une flèche allant de haut en bas, avec un symbole plus en haut de la flèche et un symbole moins en bas. — **Figure 8**. **Structure du titanate de baryum ou BaTiO₃ qui est ferroélectrique**. **À droite**, lorsque le cristal perd en symétrie, les ions positifs (baryum Ba²⁺ et titane Ti⁴⁺) sont décalés vers le haut, sans que les ions négatifs (oxygène O^2-) ne bougent. Les charges positives sont alors « plus haut » que les charges négatives et on a une directionnalité électrique.

Dans cette publication, l’équipe de J. E. Spanier a étudié des cristaux ferroélectriques qui permettent de dépasser la limite de Schockley-Queisser, mais ces derniers présentent un problème de taille. D’une part, leur bande interdite est grande par rapport à celle du silicium, ce qui limite grandement le rendement de conversion (inférieure à 0,0001 % !) ; et d’autre part, on s’aperçoit que les photons sont absorbés dans le matériau sur une faible épaisseur au-delà de laquelle ils disparaissent tous ! Une grande partie de l’épaisseur du matériau est donc totalement inutile pour la conversion puisqu’elle ne reçoit pas de photons, ce qui nuit grandement au calcul d’efficacité… Mais qu’à cela ne tienne, au lieu d’utiliser de gros cristaux, il suffit d’avoir un matériau sous forme de film mince et ainsi toute la lumière est utilisée ! L’équipe de recherche a alors réussi à multiplier l’efficacité par plus de dix mille pour atteindre 4,8 % [*****] ! Cela peut paraître peu, mais c’est tout de même un dépassement de la limite de Schockley-Queisser de 50 % pour le matériau en question !

Les matériaux de demain ?

Les ferroélectriques sont des matériaux d’avenir pour la récupération d’énergie. Cependant, ils n’ont pas encore atteint le marché et sont toujours bloqués dans les laboratoires de recherche. Ceci est notamment dû à leur bande interdite très large par rapport aux semiconducteurs de l’effet photovoltaïque classique. Mais pas de panique ! Les pistes pour réduire la bande interdite sont nombreuses [2], et les interactions entre la lumière et les ferroélectriques sont porteuses de nombreuses autres applications dans l’électronique ou dans la mécanique de précision [3, 4]. Ils ont d’ailleurs déjà été mis sur le marché dans un autre domaine qui vous parlera sûrement : ils sont utilisés par exemple dans la mémoire de la PlayStation 2 [5] ! Alors, bien que l’effet photovoltaïque anormal soit plutôt pour après-demain, les ferroélectriques ont déjà clairement leur place dans les systèmes d’aujourd’hui.

[*] La lumière est une onde, au même titre que le son. On peut alors comparer la couleur de la lumière à la hauteur d’un son. La lumière bleue correspond à un son plus aigu, tandis que la lumière rouge correspond à un son plus grave. Pour le son comme pour la lumière, une fréquence plus élevée correspond à une énergie plus grande. Cela correspond dans un cas à une couleur plus bleue, et dans l’autre à un son plus aigu.

[**] Le semiconducteur que l’on trouve le plus couramment est le silicium. C’est le constituant principal des panneaux solaires, mais pas seulement ! En effet, la plupart de notre électronique est basée sur le silicium, on en trouve donc tout autour de nous.

[***] Pour avoir un cristal de symétrie adaptée, il faut a priori aussi changer la composition.

[****] Les ferroélectriques sont semblables aux aimants, qui ont une directionnalité magnétique (pôles nord et sud de l’aimant) ; ici c’est une directionnalité électrique.

[*****] Les scientifiques ont eu recours à d’autres astuces pour arriver jusque-là, en jouant notamment sur l’efficacité des contacts électriques.

[1] Voir site de l’IRDEME : https://www.irdeme.org/

[2] Hao S., et al., Optical absorption by design in a ferroelectric: co-doping in BaTiO₃. Journal of Materials Chemistry C, 2021. DOI : 10.1039/D1TC04250E. [Publication scientifique]

[3] Guo J., et al., Recent Progress in Optical Control of Ferroelectric Polarization. Advanced Optical Materials, 2021. DOI : 10.1002/adom.202002146. [Review]

[4] Matzen S., et al., Tuning Ultrafast Photoinduced Strain in Ferroelectric-Based Devices. Advanced Electronic Materials, 2019. DOI : 10.1002/aelm.201800709. [Publication scientifique]

[5] Pour en savoir plus : https://en.wikipedia.org/wiki/Ferroelectric_RAM [en anglais].

Publié le 27/02/2022

Gaëlle Vitali-Derrien/Papier-Mâché/CC BY-NC-SA 4.0 2022

Texte et images, à l’exception des images soumises à droits d’auteurs différents : voir au cas par cas en légende.

De nouveaux matériaux pour un phénomène inédit

Écriture : Gaëlle Vitali-Derrien
Relecture scientifique : Grégory Gredat et Charles Paillard
Relecture de forme : Eléonore Pérès et Camille Petitfils

Temps de lecture : environ 20 minutes.
Thématiques : Matière condensée et Photonique (Physique)

Publication originale : Spanier J. E., et al., Power conversion efficiency exceeding the Shockley–Queisser limit in a ferroelectric insulator. Nature Photonics, 2016. DOI : 10.1038/nphoton.2016.143

Le photovoltaïsme, l’énergie éolienne ou encore l’hydroélectricité sont des alternatives prometteuses pour s’affranchir des énergies fossiles. L’enjeu est colossal dans notre société si énergivore, et la recherche pour rendre ces méthodes viables est particulièrement active. En effet, bien que les panneaux photovoltaïques semblent bien implantés dans notre quotidien, leurs performances énergétiques peuvent encore être largement améliorées. Cependant, l’effet photovoltaïque tel qu’on le connaît souffre de limitations physiques intrinsèques et s’en affranchir demande un véritable changement de paradigme. Un nouvel effet, à la physique différente, est découvert dans les années 1960 [1]. Il apparaît alors comme la solution à notre problème : on l’appelle effet photovoltaïque anormal. Pour bien se rendre compte des limitations de l’effet classique et des nouvelles possibilités qu’offre l’effet anormal, il faut comprendre les phénomènes physiques qui rendent possible l’effet photovoltaïque.

Mais qu’est-ce que l’effet photovoltaïque ?

Avant que je ne m’étende sur l’effet photovoltaïque anormal, il convient de clarifier quelques points au sujet de l’effet photovoltaïque normal, avec les panneaux bleus. D’ailleurs, savez-vous en quoi sont faits ces fameux panneaux ? L’effet photovoltaïque, qui permet de convertir la lumière en électricité, prend place dans une catégorie de matériaux spécifique : les semiconducteurs. On les rencontre au quotidien car ils sont présents dans la plupart de nos systèmes électroniques. Ce qui les rend particulièrement intéressants, c’est la répartition énergétique de leurs électrons. Dans les solides cristallins, ces électrons ont des énergies bien spécifiques : elles sont réparties sous forme de bandes. En effet, la situation d’un électron dans un cristal est à mi-chemin entre celle d’un électron libre qui peut avoir un continuum d’états différents et celle d’un électron lié à un atome qui n’a accès qu’à des valeurs discrètes. La répartition des électrons dans ces bandes rend compte des spécificités du matériau que l’on considère (Figure 1).

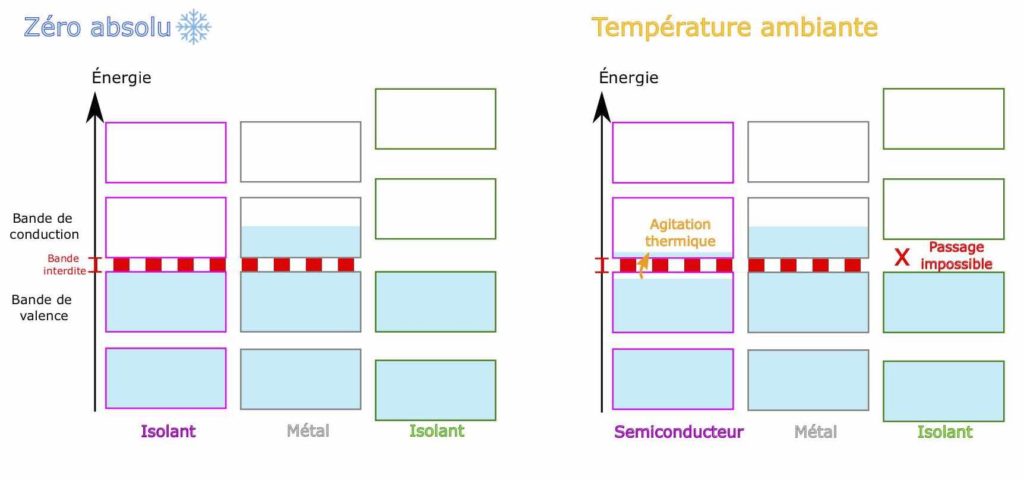
Dans le cas des semiconducteurs, la bande peuplée de plus haute énergie est appelée bande de conduction (les électrons y deviennent des électrons libres et ils peuvent se déplacer dans le cristal). Elle est séparée de la bande d’énergie inférieure, la bande de valence, par ce qu’on appelle la bande interdite (Figures 1 et 2). Les semiconducteurs ont une propriété très importante : les électrons de leur bande de valence peuvent passer la bande interdite pour atteindre la bande de conduction, laissant derrière eux des lacunes que l’on appelle tout simplement… des trous. Un électron étant chargé négativement, un trou (un manque d’électron) est donc chargé positivement. On a alors deux types de porteurs de charge que l’on peut exploiter.

Mais comment un électron peut-il passer de la bande de valence à la bande de conduction ? Pour ce faire, il a besoin d’un apport d’énergie. Comme vu en Figure 1, la température peut permettre d’apporter une énergie suffisante pour permettre aux électrons de passer dans la bande de conduction, transformant ainsi le matériau isolant au zéro absolu en semiconducteur. Mais cet apport d’énergie peut aussi se faire tout simplement par illumination !

Lumière sur les semiconducteurs

La lumière est composée de photons. Lorsqu’un photon dont l’énergie outrepasse la bande interdite arrive sur le matériau semiconducteur, il est absorbé. Son énergie permet alors à un électron de la bande de valence de passer dans la bande de conduction : on parle d’effet photoélectrique interne.

Si le photon a une énergie trop faible, le processus ne peut pas avoir lieu. Si l’énergie est grande par rapport à la bande interdite, alors l’électron atteindra de plus hautes énergies à l’intérieur de la bande de conduction. On parle alors d’électron chaud. L’électron chaud finira par perdre de l’énergie en interagissant avec son environnement pour atteindre le minimum de la bande de conduction (Figure 2). On a ici la première limitation de l’effet photovoltaïque normal : il ne permet pas d’utiliser efficacement tous les photons incidents.

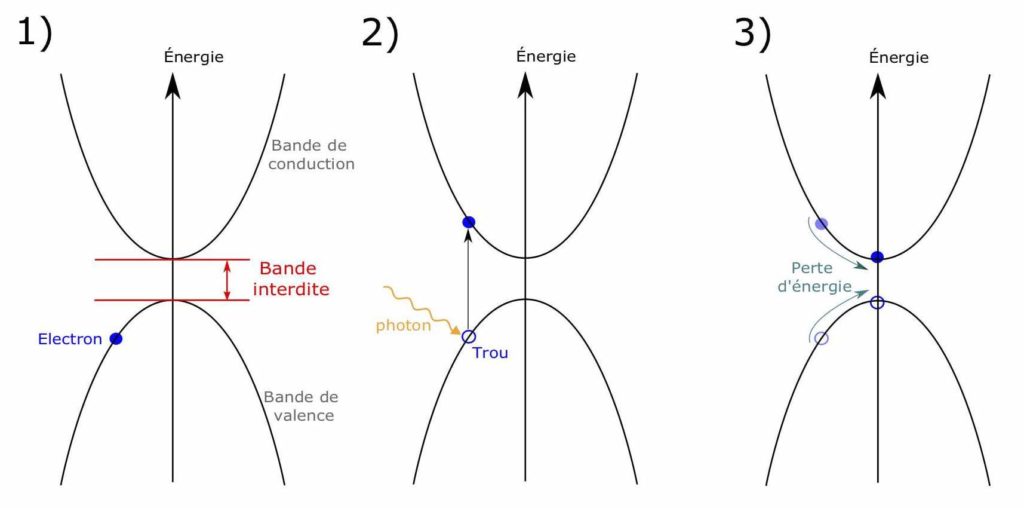
Graphique en trois parties : gauche (1), milieu (2) et droite (3). Pour chaque partie, un axe des ordonnées indique l’énergie, et il y a deux courbes en cloche : une décroissante puis croissante (tournée vers le haut), qui se trouve au-dessus d’une croissante puis décroissante (tournée vers le bas). Le minimum de la courbe du dessus est à la même abscisse que le maximum de la courbe du dessous. L’espace en ordonnée entre ces deux valeurs est noté « bande interdite ». La courbe du dessus est notée « bande de conduction » et la courbe du dessous « bande de valence ». À gauche en 1), un point bleu foncé, noté « électron », se trouve à droite sur la courbe en cloche du bas. Au milieu en 2), une flèche jaune, notée « photon », pointe vers l’emplacement du point. À la place d'un point bleu, il y a maintenant un cercle bleu foncé vide à l'intérieur, noté « trou ». Une flèche pointe sur la même abscisse mais sur la courbe en cloche du dessus. Le point bleu est maintenant à cet endroit. À droite en 3), le point et le cercle sont au même endroit que pour 2), mais ils sont d'une couleur plus claire. Des flèches pointent respectivement de l’emplacement du point jusqu’au minimum de la courbe du haut et de l’emplacement du cercle jusqu’au maximum de la courbe du bas, les flèches sont notées « perte d’énergie ». Un point bleu foncé et un cercle bleu foncé s’y trouvent respectivement. — **Figure 2. Schéma du processus de conversion d’un photon incident en paire électron-trou.** Les bandes d’énergie sont représentées de manière plus réaliste ici, par des arcs plutôt que par les rectangles de la Figure 1 . 1) Un électron se trouve dans la bande de valence. 2) Un photon permet à l’électron d’atteindre la bande de conduction, laissant derrière lui un trou. 3) L’électron et le trou perdent de l’énergie par interaction avec leur environnement pour atteindre le bas de la bande de conduction et le haut de la bande de valence respectivement.

La lumière permet donc de générer des porteurs de charge dans les semiconducteurs. Cependant, cela ne suffit pas à générer de l’électricité : il ne faut pas oublier que l’électricité, c’est des porteurs de charge en mouvement ! Il est possible d’utiliser des dispositifs qui permettent de séparer les porteurs et ainsi de générer de l’électricité sous illumination. Cependant, tous ces systèmes sont limités par un important paramètre : la tension générée par la lumière dans ces dispositifs ne peut pas dépasser la bande interdite.

En effet, les semiconducteurs ne peuvent utiliser efficacement que les photons dont l’énergie est supérieure à leur bande interdite. Comme illustré avec la Figure 3, ils ne peuvent utiliser qu’une partie du rayonnement solaire pour créer des porteurs de charges. Une fois ces porteurs créés, il faut encore avoir recours à d’autres dispositifs pour en extraire de l’électricité exploitable.

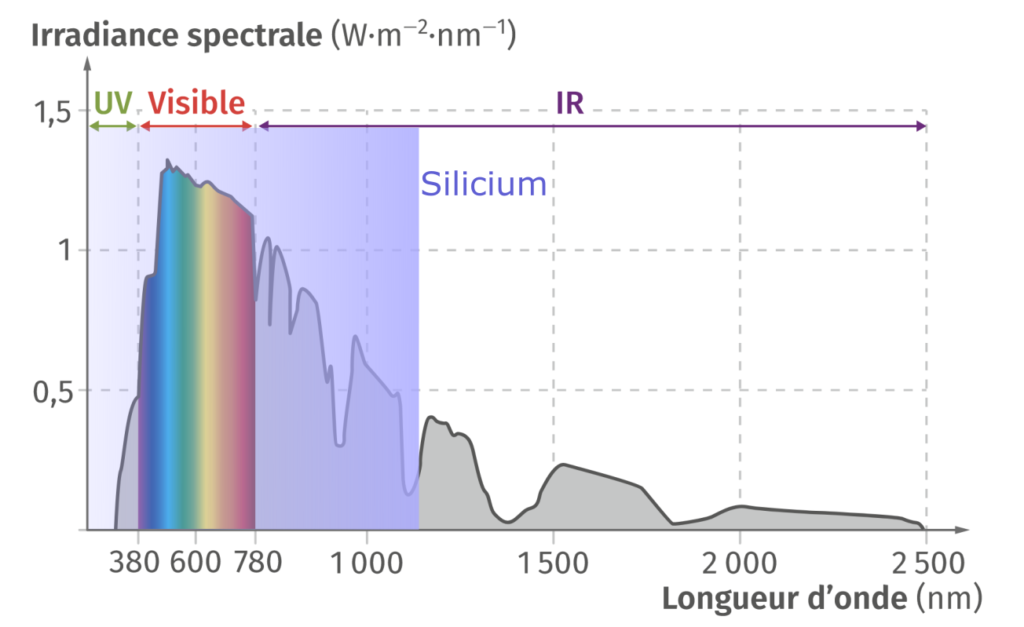
Graphique. L’axe des abscisses est la longueur d’onde (nanomètre) allant de 0 à 2500 ; l’axe des ordonnées est l’irradiance spectrale (watt par mètre carré par nanomètre) allant de 0 à 1,5. Entre 0 et 380 nanomètres se trouvent les ultraviolets, entre 380 et 780 nanomètres le rayonnement visible, et enfin au-dessus se trouve le rayonnement infrarouge. L’irradiance est nulle jusqu’à environ 300 nanomètres où elle augmente fortement pour attendre 1,25 aux alentours de 500 nanomètres. Elle décroît ensuite de manière monotone, avec quelques creux. Une partie du graphique est bleutée, entre 0 et 1100 nanomètres. Le bleu est un fondu, allant de très opaque à 1100 nanomètres à transparent à 0 nanomètres. — **Figure 3. Spectre solaire au niveau de la mer.** La partie dégradée bleutée contient les photons pouvant être absorbés par le silicium, un semiconducteur très couramment utilisé dans l’industrie (bande interdite : 1,12 eV). Du fait d’autres phénomènes physiques, l’absorption du silicium diminue dans l’ultra-violet. Crédit : adaptée depuis Lelivrescolaire.fr/CC BY-NC-SA

Si l’énergie est sous la bande interdite, ça ne fonctionne pas ; si elle est au-dessus, la différence avec cette dernière est perdue… ça en fait de l’énergie non exploitée ! En effet, sur la Figure 3, toute la partie du spectre solaire non bleutée est tout bonnement perdue. Et cette limitation est fondamentale, dictée par les lois de la physique. On l’appelle la limite de Shockley-Queisser (S-Q), elle dépend de la bande interdite du matériau que l’on considère. Un matériau avec une bande interdite plus étroite aura une zone bleutée plus étendue sur la Figure 3.

La bande interdite est à la base de nombreuses performances dans les semiconducteurs. Les meilleurs ici sont ceux pour lesquels elle est plus étroite [**] : ils peuvent convertir une plus large gamme de photons en porteurs de charge. Cependant, même en considérant le silicium que l’on utilise pour les panneaux classiques, l’efficacité de la conversion, c’est-à-dire le nombre d’électrons de conduction par photon incident, de la lumière du Soleil plafonne à 33 % !

Retour à l’anormal

La limitation fondamentale de l’effet photovoltaïque normal vient du fait que les photons incidents sont utilisés uniquement pour créer des paires électrons-trous, quand leur énergie est au-delà de la bande interdite. Si l’on veut dépasser cette limite, il faut soit utiliser les électrons de plus faible énergie, soit mettre à profit les électrons qui sont devenus chauds. L’utilisation des photons incidents n’est pas le seul problème que j’ai souligné jusqu’ici : la tension est elle-aussi limitée (par la bande interdite) et les porteurs doivent être extraits par l’intermédiaire de dispositifs extérieurs. Ce sont donc autant de limitations qui rendent l’effet normal peu efficace et surtout peu viable à long terme. Existe-t-il alors un nouveau phénomène physique, qui réglerait ces deux problèmes ? (Attention spoiler : oui, c’est l’effet photovoltaïque anormal !)

Si l’on veut mettre à profit les photons incidents de plus basse énergie il y a essentiellement un paramètre sur lequel jouer : c’est la bande interdite. Cette dernière dépend du matériau que l’on considère. Il est possible de la modifier légèrement en dopant le matériau : on y introduit des composés en très petite quantité qui vont modifier ses propriétés. Cependant, cette technique est jeune et les nouveaux composés peuvent déstabiliser les propriétés du matériau initial [3]. Il semble alors plus prometteur d’utiliser les électrons chauds, dont l’énergie est perdue à l’intérieur du matériau. Quelles propriétés pourraient alors permettre d’utiliser l’énergie de ces électrons chauds et, qui sait, de générer aussi une tension supérieure à la bande interdite, ce sans même appliquer d’autre stimulation que la lumière ? Pour comprendre le mécanisme à l’œuvre derrière l’effet photovoltaïque anormal, il faut s’intéresser à la structure géométrique des cristaux semiconducteurs. En effet, lorsque le cristal perd en symétrie (comme dans la Figure 4), de nouvelles propriétés peuvent apparaître.

Lorsque le cristal perd en symétrie, toutes ses directions ne sont plus équivalentes. Certaines propriétés ont alors une direction privilégiée : on voit par exemple que sur la maille de droite de la Figure 4 les directions horizontale et verticale ne sont plus symétriques, cela peut favoriser certains phénomènes dans une direction plutôt que dans l’autre. C’est le cas de la quantité de mouvement des électrons et des trous, qui n’est alors plus distribuée de la même manière. Cela signifie que les porteurs de charge générés par illumination tendent à se mouvoir préférentiellement dans une direction plutôt qu’une autre… On assiste bien à la création d’un courant simplement grâce à la lumière, c’est l’effet photovoltaïque anormal [***] ! Cet effet a lieu pendant que les porteurs sont encore chauds. Une fois qu’ils ont atteint le minimum de la bande de conduction ou le maximum de la bande de valence, ils perdent leur direction privilégiée et on repasse à l’effet photovoltaïque normal tel qu’il est décrit dans la Figure 2. La perte d’énergie se fait dans le matériau sur une longueur caractéristique $l_0$ . Elle dépend du matériau, mais vaut en général quelques dizaines de nanomètres. Cette distance joue un rôle extrêmement important dans la récupération de l’énergie.

L’effet anormal permet donc d’utiliser les électrons chauds du semiconducteur et de les séparer sans dispositif extérieur. Une fois qu’ils ont perdu leur énergie et qu’ils ont atteint le minimum de la bande de conduction, ils restent utilisables et l’on repasse à l’effet photovoltaïque normal (Figure 2). Cependant, lorsque l’on illumine un matériau avec des photons d’énergie supérieure à la bande interdite, ces derniers ne pénètrent que sur une épaisseur limitée. En effet, ils sont petit à petit absorbés en créant des porteurs, si bien qu’au bout de quelques dizaines de nanomètres il n’en reste plus un seul. Les phénomènes physiques que j’ai mentionnés jusqu’ici ne se jouent alors essentiellement qu’en surface. On pressent ici qu’en plus de la structure, la taille du cristal va aussi jouer un rôle important !

Les chercheur·ses ont alors mesuré l’efficacité de la conversion d’énergie dans différents cristaux non centrosymétriques (Figure 4). Dans cette publication, J. E. Spanier et son équipe ont étudié des cristaux de titanate de baryum, noté BaTiO₃. Ils ont soigneusement calculé l’efficacité de conversion et elle s’élève à… 10^-4-10^-5 %. Pour un effet révolutionnaire, on a vu mieux ! Le problème ici est que ces cristaux, de taille millimétrique, étaient de dimension beaucoup trop grande, comparé à $l_0$ (nanométrique), donc seule une infime partie des électrons pouvaient participer à l’effet photovoltaïque anormal. Les auteur·rices ont donc décidé de travailler sur des films de 20 et 40 nm d’épaisseur : les porteurs chauds ainsi créés à la surface du matériau sont donc tous mis à contribution.

En réduisant la taille de l’échantillon sur lequel ils·elles travaillent, les auteur·rices arrivent d’une part à utiliser efficacement tous les photons incidents, et d’autre part à utiliser tous les porteurs que ces photons auront générés. Et en effet : l’efficacité s’élève alors à quelques pourcents. C’est tout de même un gain de cinq ordres de grandeur ! Cela reste encore peu face aux 33 % du silicium, mais l’efficacité par rapport à un matériau de même bande interdite est décuplée. L’effet anormal n’en est encore qu’à ses débuts, et bien qu’ils soient prometteurs, il reste encore beaucoup de chemin aux scientifiques et aux ingénieur·es pour l’optimiser !

Jusqu’ici, on sait que la structure atomique du cristal permet d’utiliser les porteurs photogénérés quelle que soit leur énergie et que pour utiliser tous ces porteurs ,il faut que ledit cristal soit sous forme de couche mince. Maintenant, est-il encore possible d’optimiser la réponse du matériau ? Quels leviers restent-ils aux chercheur·ses afin de continuer à améliorer les performances photovoltaïques ?

Il existe une autre dimension avec laquelle les auteur·rices ont pu jouer. Cette fois-ci il ne s’agit pas de l’échantillon en lui-même, mais de ce qui permet d’établir le contact électrique avec ce dernier et d’extraire le courant photovoltaïque : les électrodes. Il est courant d’utiliser une configuration en « sandwich » : l’échantillon photovoltaïque est pris entre deux plaques métalliques. Ici, les autrices et auteurs ont remplacé l’une des électrodes par une pointe de microscope à force atomique (AFM). Il s’agit d’une pointe extrêmement fine dont l’extrémité est composée d’un seul atome ! Avec ce genre de dispositif, l’efficacité apparente [****] dépasse l’unité. On parle de régime amélioré par pointe.

Techniques de pointe(s)

Le régime amélioré par pointe n’a pas lieu dans tous les matériaux qui donnent lieu à un effet photovoltaïque anormal. Par exemple, les auteur·rices n’ont pas observé d’amélioration lorsqu’ils·elles ont utilisé une électrode pointue sur un cristal de phosphure de gallium GaP, dans lequel l’effet anormal a bien lieu. Cette amélioration était par contre présente avec des cristaux de BaTiO₃. Pourtant, ces deux matériaux sont bien sujets à l’effet photovoltaïque anormal… Pourquoi donc l’amélioration a-t-elle lieu dans certains cristaux plutôt que dans d’autres ?

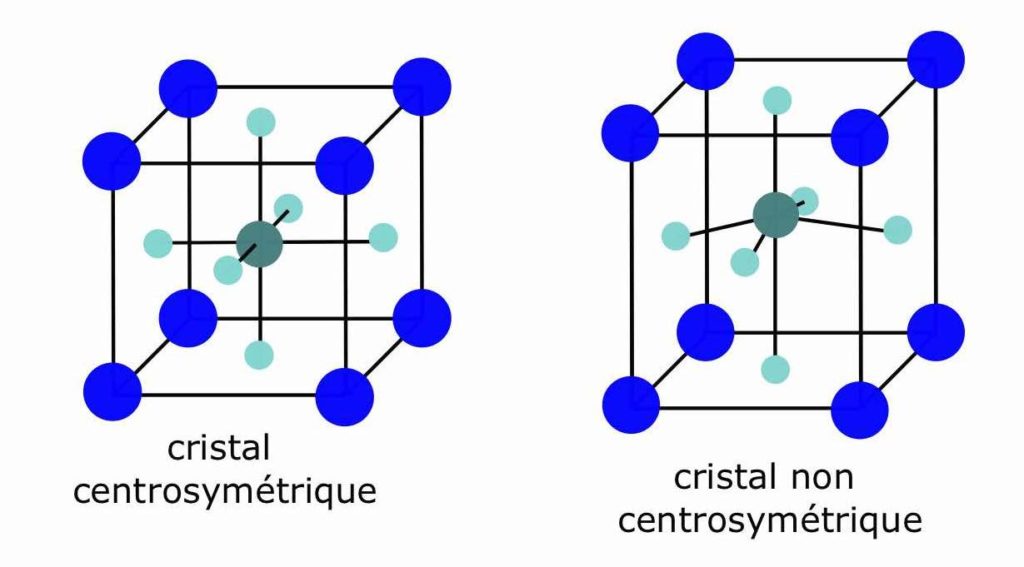
Pour rappel, l’effet anormal prend place dans des cristaux qui ont perdu en symétrie. Pour certains d’entre eux cette perte de symétrie amène aussi d’autres effets. On observe par exemple que pour quelques cristaux ioniques, le barycentre des charges positives (dues aux cations) ne correspond plus à celui des charges négatives (dues aux anions) lorsque la symétrie est brisée… Le cristal possède alors, spontanément, une polarisation non nulle (Figure 5) que l’on peut d’ailleurs contrôler en appliquant un champ électrique sur le cristal ! On parle alors de matériau ferroélectrique.

Similaire à la Figure 4, mais les points sur les faces des cubes sont ici rouges. Près des points bleus, aux sommets des cubes, est écrit « Ba2+ » ; près des points rouges sur les faces est écrit « O2- » ; près du point vert au centre est écrit « Ti4+ ». Le long de l’arête étirée du « cube » de droite, il y a une flèche allant de haut en bas, avec un symbole plus en haut de la flèche et un symbole moins en bas. — **Figure 5.** **Schéma d’une maille de BaTi0₃ centrosymétrique (gauche) et non centrosymétrique (droite).** Les cations (baryum et titane) sont décalés vers le haut tandis que les anions (oxygène) sont décalés vers le bas. Il apparaît alors une polarisation (flèche jaune). La maille utilisée dans le schéma est dite maille perovskite [*****].

La polarisation dans le cristal ferroélectrique est comme une direction privilégiée pour les phénomènes électriques. Cette sensibilité accrue vis-à-vis de l’électricité est la clé pour comprendre le régime amélioré par pointe.

En effet, comment expliquer qu’en changeant la forme de l’électrode sans même modifier l’échantillon, on arrive à améliorer ses performances ? Pour tenter de comprendre ce phénomène, l’équipe de J. E. Spanier a eu recours à différentes pointes d’AFM de diamètres variables. Il semble que le diamètre de la pointe n’ait pas d’influence notable sur les performances du système. L’amélioration semble alors gouvernée par une autre dimension caractéristique.

Près de l’électrode, et dans une sphère de rayon $l_0$ , de nombreux porteurs de charges très énergétiques sont collectés (Figure 6). L’espace autour de la pointe est donc rempli de charges. Grâce à la polarisation déjà présente dans le cristal, ces charges vont former dans la sphère un champ électrique très intense. Les porteurs soumis à ce champ intense vont alors ioniser les atomes du cristal : en les percutant, ils leur arrachent des électrons, et créent ainsi de nouveaux porteurs ! On augmente alors le nombre de porteurs, ce qui donne bien lieu à une efficacité apparente accrue. En utilisant un matériau ferroélectrique en régime amélioré par pointe, l’équipe de J. E. Spanier a réussi à atteindre une efficacité de conversion de 4,8 %. Pour un matériau avec une telle bande interdite, cela revient à dépasser la limite S-Q d’environ 50 % ! La recherche vise maintenant à diminuer la bande interdite des matériaux soumis à l’effet anormal. Si l’on arrive à atteindre la bande interdite du silicium, on pourra viser une efficacité de conversion proche de 50 %, soit plus du rendement moyen de la production globale d’électricité [4] !

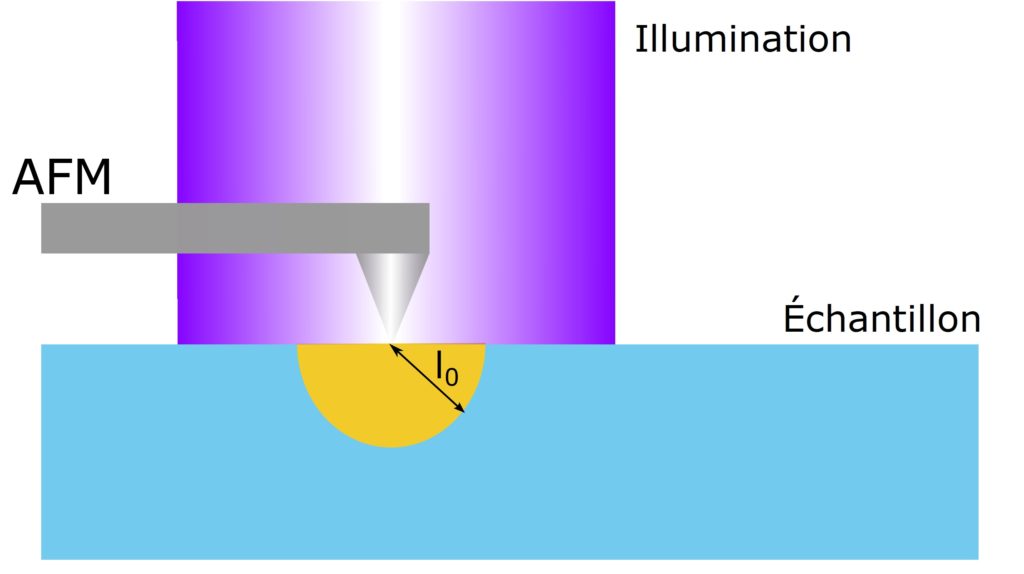
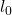**Figure 6**. Schéma de la formation d’une sphère de porteurs chauds de rayon $l_0$ dans l’échantillon sous illumination au contact de la pointe de l’AFM.

Jusqu’ici, les auteur·rices ont réussi à mesurer un courant et une tension en connectant la pointe d’un AFM à un matériau ferroélectrique soumis à une illumination. Cependant, comment confirmer qu’il s’agit bien de l’effet photovoltaïque anormal ?

La même mesure a été faite dans deux matériaux : le titanate de baryum BaTiO₃, un cristal ferroélectrique, et le titanate de strontium SrTiO₃, un cristal centrosymétrique, dont les structures de bandes sont très similaires [******]. Les chercheur·ses ont alors mesuré le courant en circuit fermé $I_{SC}$ et la tension en circuit ouvert $V_{OC}$ , avec et sans illumination. L’énergie du rayonnement est supérieure à la bande interdite des deux matériaux. Dans le cristal ferroélectrique, le courant $I_{SC}$ sous illumination est mille fois supérieur à celui mesuré dans le noir, tandis qu’aucun courant n’est mesuré dans le cristal symétrique. De même, sous illumination, les auteur·rices ont mesuré une tension $V_{OC}$ bien supérieure à la bande interdite dans le premier cristal, mais rien de probant dans le second.

On sait maintenant que l’on peut générer efficacement de l’électricité par effet photovoltaïque anormal dans un matériau ferroélectrique grâce à une pointe d’AFM. Cependant, il est possible d’aller encore plus loin ! En effet, la pointe de l’AFM permet de récupérer les charges dans une sphère de rayon $l_0$ autour d’elle. Pourquoi alors ne pas utiliser plusieurs pointes, espacées de $l_0$ , sur toute la surface du matériau ? C’est la question que l’équipe de recherche s’est posée. Les scientifiques ont alors réalisé un quadrillage de 24 pointes (8 rangées de 3 pointes) et ont mesuré la tension, le courant et la fraction de puissance lumineuse convertie en puissance électrique.

Le courant mesuré avec un quadrillage de pointes est proportionnel au courant mesuré avec une pointe unique. Cela permet d’une part de confirmer l’hypothèse selon laquelle une pointe permet de collecter les porteurs autour d’elle, mais aussi de donner une piste pour améliorer grandement la collecte des porteurs. Ce dispositif permet de convertir 3,9 % de la puissance lumineuse en puissance électrique, c’est une efficacité remarquable dans ce domaine !

Reconversion énergétique

Les cristaux ferroélectriques sont très prometteurs pour la récupération d’énergie lumineuse. Leur physique est intrinsèquement différente de celle des semiconducteurs et ils peuvent ainsi s’affranchir des limitations fondamentales qui planent sur ces derniers. Cependant, comme nous l’avons vu, la recherche en est à encore à ses débuts et l’efficacité de la conversion n’est encore que de quelques pourcents, surtout si l’on compare aux 33 % de silicium ! Par ailleurs, il y a encore de nombreux obstacles à l’utilisation massive des ferroélectriques pour le photovoltaïsme : ils doivent notamment s’intégrer dans des structures qui sont conçues pour le silicium, et résister aux mêmes contraintes (mécaniques, thermiques, etc.). Il reste donc encore beaucoup de défis à relever !

Bien que l’effet photovoltaïque anormal soit d’un grand intérêt scientifique, il ne représente pas la seule alternative pour dépasser la limite S-Q. D’autres techniques sont employées, certaines d’ailleurs toujours basées sur le silicium. Ces techniques ainsi que leurs performances ont été consignées par le National Renewable Energy Laboratory. Enfin, la recherche sur les cristaux ferroélectriques constitue aussi une ouverture vers de nouveaux matériaux et de nouveaux dispositifs. On peut citer par exemple les matériaux hybrides organiques-inorganiques aux structures cristallines similaires à BaTiO₃ (la structure perovskite) : bien qu’ils obéissent à l’effet photovoltaïque normal, ils permettent une efficacité de conversion supérieure à 25 % ! [5]

Finalement, les cristaux ferroélectriques ont attiré l’attention grâce à leurs propriétés photovoltaïques, mais ils semblent maintenant également prometteurs dans d’autres domaines ! Leurs propriétés électriques et leurs interactions complexes avec la lumière les rendent particulièrement intéressants dans le domaine de l’électronique ou de l’optique. La recherche sur ces matériaux n’a donc pas fini de surprendre !

[*] Un semiconducteur est donc un isolant à 0 K ! C’est là la différence fondamentale entre les semiconducteurs et les isolants. Pour ces derniers, si l’on veut apporter l’énergie nécessaire pour faire passer des électrons de valence dans la bande de conduction, on finit juste par les faire fondre !

[**] Attention à ne pas trop réduire la taille de la bande interdite : si elle est trop étroite, tous les électrons peuvent la passer simplement par agitation thermique…

[***] L’asymétrie cristalline ne permet pas d’expliquer complètement l’effet photovoltaïque anormal. En effet, certaines contributions sont intrinsèquement quantiques.

[****] C’est le rapport du flux d’électron à travers une surface par le flux de photons .

[*****] La structure perovskite se retrouve dans de nombreux matériaux, notamment les oxydes de formule chimique ABO₃ (avec A et B des cations). Ces cristaux représentent un intérêt technologique majeur en raison de leurs propriétés multiphysiques : le choix des cations A et B permet d’obtenir des cristaux qui peuvent aussi bien être ferroélectriques que supraconducteurs !

[******] D’ailleurs ces deux matériaux sont des isolants !

[1] Fridkin V.M., Bulk Photovoltaic Effect in Noncentrosymmetric Crystals. Cristallography reports, 2001. DOI : 10.1134/1.1387133. [Publication scientifique]

[2] Kittel C., « Introduction to Solid State Physics 8th edition ». Wiley, 2005. ISBN : 978-0-471-41526-8. [Livre de science]

[3] Shyamashis D., et al., Designing a Lower Band Gap Bulk Ferroelectric Material with a Sizable Polarization at Room Temperature. ACS Energy Letters, 2018. DOI : 10.1021/acsenergylett.8b00492. [Publication scientifique]

[4] D’après un article de Total Energies.

[5] Guo J., et al., Recent Progress in Optical Control of Ferroelectric Polarization. Advanced Optical Materials, 2021. DOI : 10.1002/adom.202002146. [Review]

Publié le 27/02/2022

Gaëlle Vitali-Derrien/Papier-Mâché/CC BY-NC-SA 4.0 2022

Texte et images, à l’exception des images soumises à droits d’auteurs différents : voir au cas par cas en légende.

La publication scientifique facile à digérer !