Chargement de l'article...
Écriture : Thibault Poignonec
Relecture scientifique : Dorian Vigoureux
Relecture de forme : Pauline Colinet et Pierre Marrec
Temps de lecture : environ 10 minutes.
Thématiques : Robotique (Ingénierie)
Publication originale : N. Hogan, Impedance Control: An Approach to Manipulation: Part I—Theory ; Part II—Implementation ; Part III—Applications. Journal of Dynamic Systems, Measurement, and Control, 1985. DOI : 10.1115/1.3140702 ; 10.1115/1.3140713 ; 10.1115/1.3140701

Bien souvent, les robots effectuent des tâches simples et répétitives dans des environnements contrôlés. Mais que se passe-t-il quand ils doivent évoluer avec un environnement complexe et délicat, que ce soit pour manipuler des fruits ou interagir avec un humain ? Comment ces constructions d’acier peuvent-elles agir avec délicatesse alors que tout semble s’y opposer ? C’est une technique appelée « commande en impédance » qui vient à la rescousse, donnant à nos amis les robots leurs gants de velours !
La commande « classique » des robots
Un robot est une machine constituée de pièces mobiles actionnées par des moteurs. En règle générale, il y a deux façons de faire bouger un robot. La première consiste à lui dire où aller et est nommée « commande en position ». La seconde consiste à lui dire quelle force appliquer sur l’environnement et est nommée « commande en force ». Ces deux méthodes permettant de contrôler un robot ont malheureusement de sérieuses limitations :
- Une commande en position consiste à actionner les moteurs jusqu’à ce que la position voulue soit atteinte, quitte à appliquer des forces très élevées. Cela ne fonctionne donc que si la position peut être atteinte, car dans le cas contraire, le robot pourrait forcer de toutes ses forces et endommager quelque chose, lui-même, voire quelqu’un !
- De façon similaire, une commande en force consiste à appliquer une force sur l’environnement. Cela peut avoir des effets imprévisibles si par exemple l’objet sur lequel les forces doivent être appliquées n’est pas présent : sans résistance exercée sur le robot, les moteurs le feront accélérer et atteindre des vitesses potentiellement élevées et dangereuses.
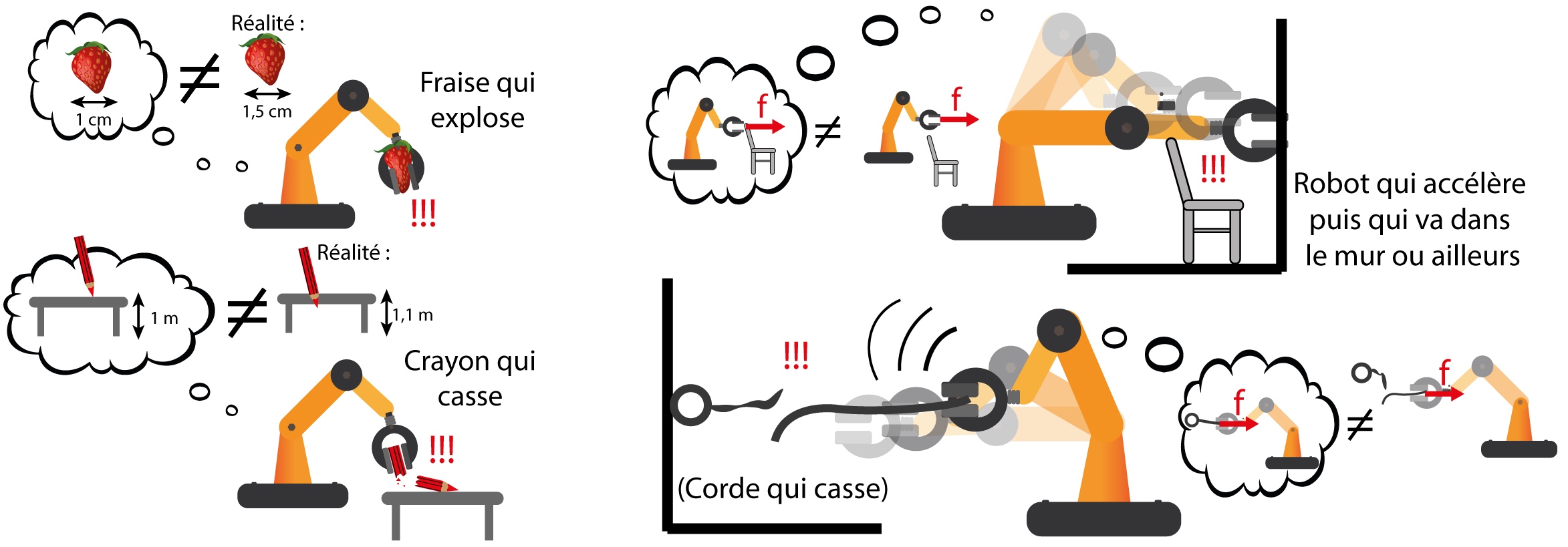
Comme illustré sur la Figure 1, les problèmes dont nous parlons sont plutôt banals pour nous les humains : prendre un fruit, écrire avec un crayon, pousser ou tirer une corde, rien de très impressionnant. Mais comment se fait-il que des problèmes apparemment aussi triviaux soient si complexes pour un robot ? La publication que nous étudions répond à cette question : les êtres vivants ont une astuce pour résoudre ces problèmes et encore mieux, c’est une astuce qu’un robot peut émuler.
Qu’est-ce qu’une impédance mécanique ?
L’impédance mécanique décrit comment un système réagit quand nous essayons de le faire bouger. Par exemple, si vous comprimez un ressort, ce ressort va s’opposer à sa déformation. La force qu’il faudra appliquer pour le déformer davantage va dépendre de la compression que vous avez déjà exercée : la force est ici proportionnelle au déplacement par rapport à la position de repos. De façon plus générale, l’impédance mécanique nous dit comment un système s’oppose au mouvement. Cela peut être illustré par trois éléments de base en mécanique qui sont :
- le ressort, pour lequel la force est proportionnelle au déplacement ;
- l’amortisseur, pour lequel la force est proportionnelle à la vitesse ;
- la masse, pour laquelle la force est proportionnelle à l’accélération.
Ces trois éléments sont illustrés dans la Figure 2 où la force nécessaire pour déplacer un objet est représentée par la flèche rouge.
| Élément mécanique | Amortisseur | Ressort | Masse |
| Illustration | 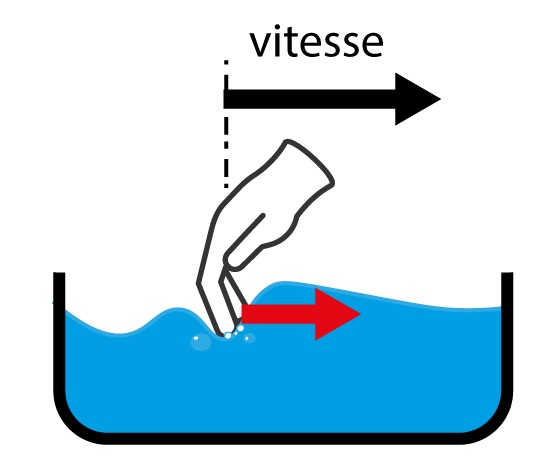 | 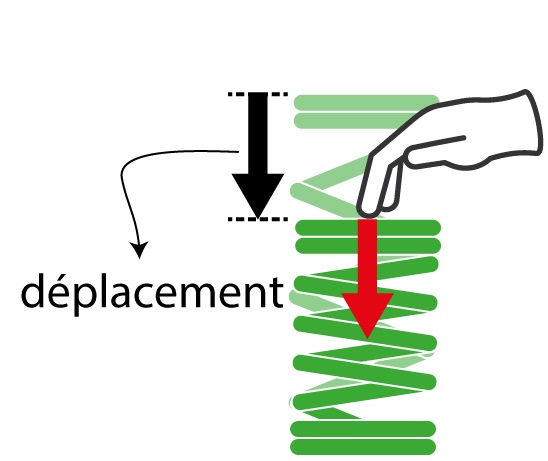 | 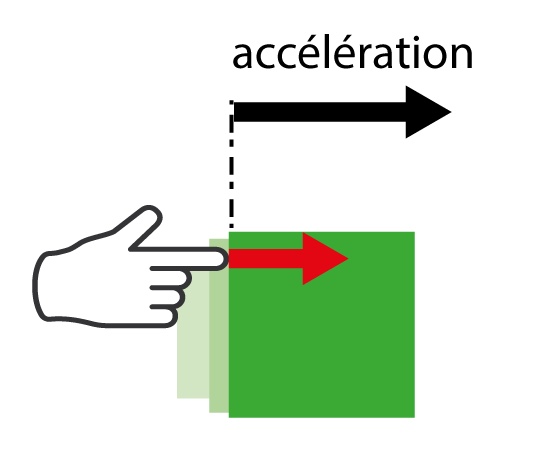 |
De nombreux objets ont une impédance mécanique qui peut être grossièrement modélisée par un assemblage de ressorts, de masses et d’amortisseurs. Par exemple, si vous voulez étudier comment votre voiture va réagir si vous roulez à 150 km/h sur un dos d’âne, vous pouvez commencer par créer un modèle. Pour ce faire, la voiture pourrait être modélisée par une masse et la suspension par un ressort et un amortisseur. Dans ce modèle, le déplacement étudié serait la hauteur d’un point fixe dans la voiture pour voir comment le conducteur serait secoué.
Les humains, experts malgré eux de l’impédance mécanique
Les êtres humains, quand ils manipulent des objets ou se déplacent, agissent de façon analogue à une impédance mécanique. Quand nous effectuons un geste, quel qu’il soit, nous ne sommes jamais totalement rigides : nous nous adaptons à l’environnement. Notre posture et notre tension musculaire permettent de régler le comportement mécanique de notre corps afin d’être plus ou moins délicat, plus ou moins rigide, voire tout simplement pour éviter de nous blesser…
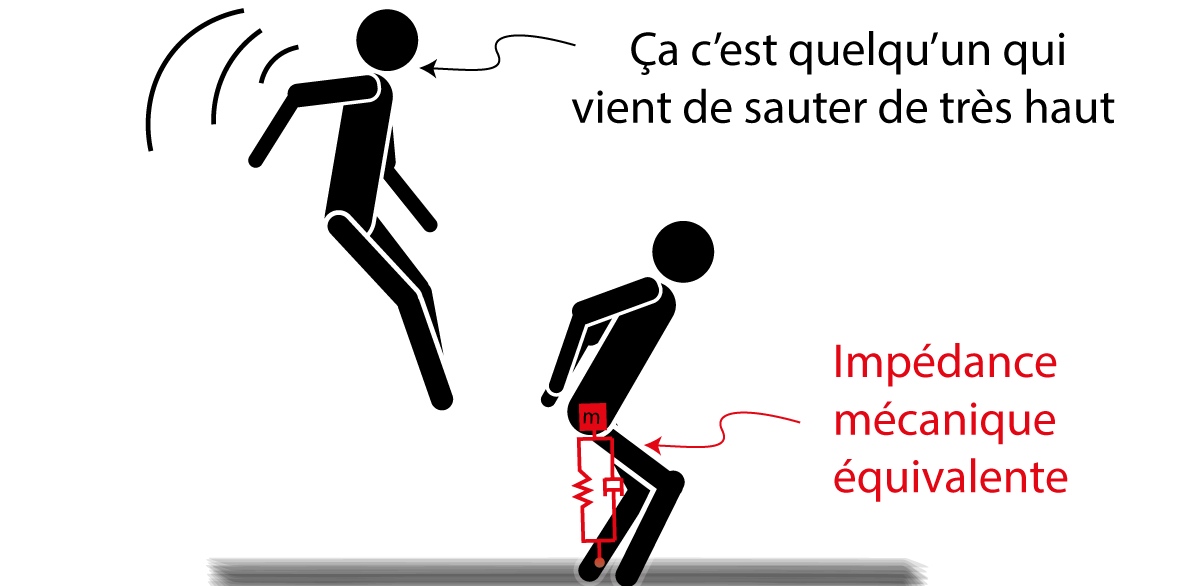
Par exemple, pour amortir une chute, il faut absorber le choc au mieux (Figure 3) ; pour écrire, il est nécessaire de garder le poignet souple et pour donner un coup de poing, il faut rigidifier le bras le plus possible. Toutes ces situations demandent des comportements mécaniques différents, c’est-à-dire une impédance mécanique différente, et nous le faisons tout le temps sans trop y penser.
La commande par impédance consiste à répliquer ce type de comportement avec un robot. Au lieu de simplement dire au robot où aller ou quelle force appliquer, nous voulons lui dire à la fois où aller et comment se comporter quand il est en contact avec un objet. De cette façon, si rien ni personne n’interagit avec le robot, il ira là où nous lui avons dit d’aller. En revanche, si quelque chose ou quelqu’un s’interpose, le comportement mécanique du robot restera adapté à la situation.
Principe général de la commande en impédance
Pour récapituler, nous souhaitons commander le robot pour que son comportement mécanique (son impédance) soit adapté à une situation où le robot doit interagir avec un objet. Le principe de la commande par impédance s’inspire des êtres vivants qui doivent évoluer dans un monde sans le casser et sans se blesser eux-mêmes. Reste à les copier…
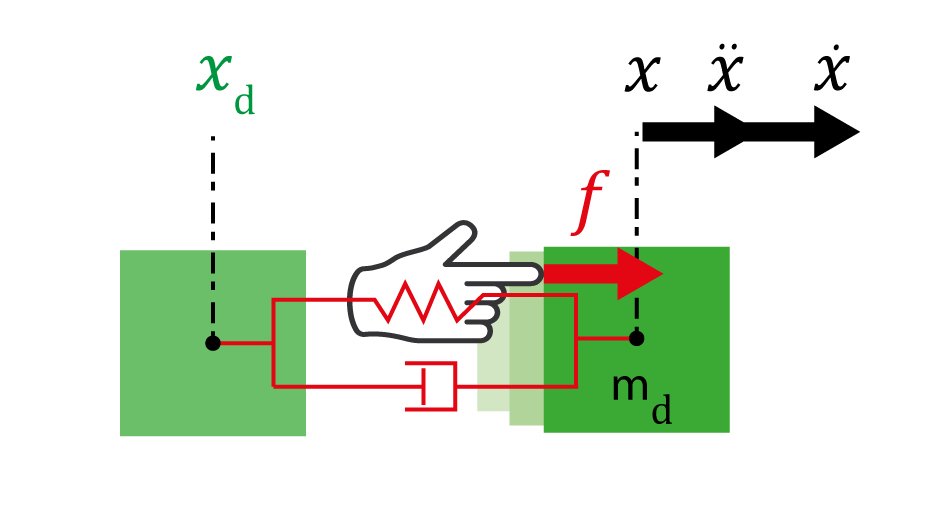
Pour commencer, il nous faut un modèle du comportement mécanique que nous souhaitons obtenir. Nous prenons le modèle « masse-ressort-amortisseur » introduit plus haut pour la voiture, car il est simple tout en restant très générique. Ce modèle nous permet de calculer la relation entre la force appliquée et le déplacement (Figure 4).
Les forces appliquées par les moteurs du robot sont calculées pour que, vu de l’extérieur, le robot se comporte exactement comme le modèle que nous avons choisi. À chaque instant, le robot mesure sa position et sa vitesse puis calcule la force qu’il doit appliquer pour se comporter de la manière choisie. Comme représenté dans la Figure 4, il est possible de définir une « position désirée » [*]. C’est la position à laquelle reviendra le robot si aucune force n’est appliquée par l’environnement (ex : le doigt disparaît dans la Figure 2).
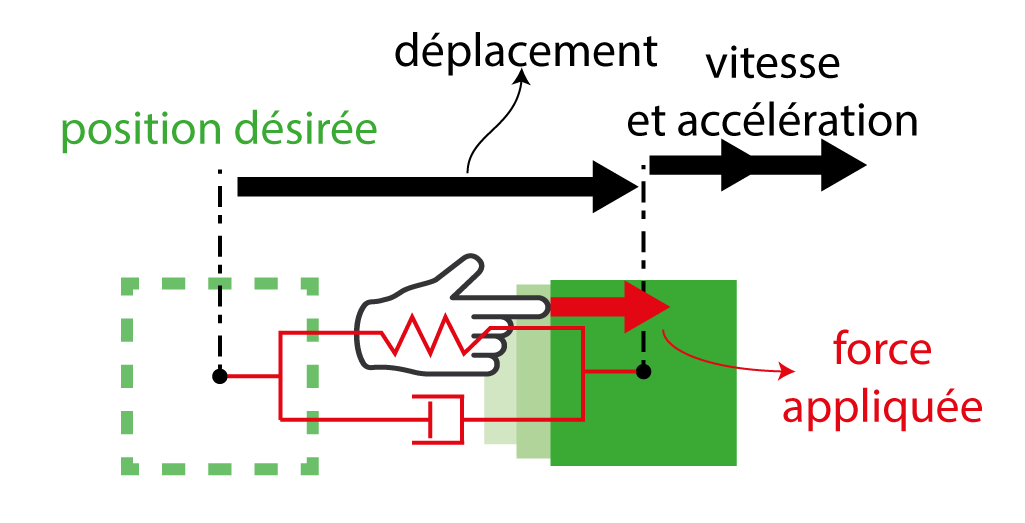
Ce n’est donc plus seulement la force appliquée par un robot ou sa position que nous souhaitons contrôler, mais bien la relation entre les deux. Un exemple d’une telle relation pourrait être : « plus on déplace le robot par rapport à une position de référence, plus la force appliquée par le robot augmente », ce qui serait modélisé par la raideur du ressort ; ou bien : « plus le robot se déplace vite, plus il va tenter de ralentir », ce qui serait modélisé par le coefficient d’amortissement de l’amortisseur (c’est-à-dire à quel point il amorti). Pour revenir aux problèmes mentionnés dans l’introduction, cela permet d’adapter l’impédance mécanique du robot telle qu’elle peut être perçue par l’extérieur. Par exemple, pour être rigide, quitte à appliquer des forces élevées, il suffit de choisir une raideur élevée, mais pour être flexible et ainsi limiter les forces, il va falloir choisir une raideur faible.
Applications & Limites
Le résultat est parfois impressionnant vu qu’on ne s’attend pas à ce qu’un robot qui pèse 30, 50, 100 voire 200 kg soit aussi flexible quand nous le poussons. Voici deux exemples en vidéo avec un robot de la marque Kuka et l’autre de Franka Emika où le comportement du robot est bien visible.
En règle générale, il faut adapter l’impédance mécanique (apparente) du robot suivant la situation. Si nous reprenons l’exemple de l’écriture à gauche de la Figure 1, il est raisonnable de dire que le crayon est très fragile. Il faudra donc que le geste du robot soit très souple pour réduire les forces et ne pas casser le crayon : la raideur choisie pour le ressort dans le modèle doit être très faible. Les forces d’interaction resteront faibles et le robot pourra faire autant de gribouillis qu’il le souhaite, sans casser le crayon.
Bien sûr, comme toute technique ou méthode, le contrôle par impédance n’est pas une solution miracle qui peut résoudre tous les problèmes. Les limites sont d’ailleurs discutées dans la partie III de la publication et il est important d’également les mentionner ici. La commande en impédance permet de moduler le comportement mécanique du robot, mais le prix à payer est que ni la force appliquée ni la position ne peuvent être imposées précisément. C’est donc un compromis entre précision et délicatesse : pour être précis il faut être très rigide alors que pour être délicat, il faut être très souple…
Ce compromis est tout de même très intéressant, d’où le succès de cette technique depuis presque 40 ans (ces travaux datent de 1985) et le fait qu’elle soit toujours d’actualité. Aujourd’hui plus que jamais, les robots interagissent avec les humains au quotidien :
- les exosquelettes pour permettre à des personnes de (re)marcher ;
- les voitures autonomes ou même l’assistance à la direction dans les voitures pour nous aider à conduire ;
- les robots qui réalisent des tâches près des humains, par exemple les robots chirurgicaux ;
- peut-être dans le futur, des robots à la maison pour faire le ménage ou la cuisine ;
- etc.
Pour conclure, la commande par impédance est une technique très utile qui complémente bien les commandes classiques en force ou en position. Elle permet à des robots qui sont par nature lourds et rigides de paraître légers et souples, ce qui, comme nous l’avons vu, est parfois très important. Ce type de commande est également une brique de base pour de nombreuses applications où l’interaction mécanique doit être maîtrisée, comme celles où les robots doivent interagir avec nous.
[*] Peut-être étendu à des scénarios où le robot a non seulement une position désirée, mais aussi une vitesse et une accélération désirées. Cela permet de réaliser des tâches telles que « va du point A au point B à une certaine vitesse ». Ce point est discuté dans la version Approfondissement.
Écriture : Thibault Poignonec
Relecture scientifique : Dorian Vigoureux
Relecture de forme : Pauline Colinet et Pierre Marrec
Temps de lecture : environ 14 minutes.
Thématiques : Robotique (Ingénierie)
Publication originale : N. Hogan, Impedance Control: An Approach to Manipulation: Part I—Theory ; Part II—Implementation ; Part III—Applications. Journal of Dynamic Systems, Measurement, and Control, 1985. DOI : 10.1115/1.3140702 ; 10.1115/1.3140713 ; 10.1115/1.3140701

Bien souvent, les robots effectuent des tâches simples et répétitives dans des environnements contrôlés. Mais que se passe-t-il quand ils doivent évoluer avec un environnement complexe et délicat, que ce soit pour manipuler des fruits ou interagir avec un humain ? Comment ces constructions d’acier peuvent-elles agir avec délicatesse alors que tout semble s’y opposer ? C’est une technique appelée « commande en impédance » qui vient à la rescousse, donnant à nos amis les robots leurs gants de velours !
La commande « classique » des robots
Un robot est une machine constituée de pièces mobiles actionnées par des moteurs et peut être commandé soit en position, soit en force. En d’autres mots, des commandes lui sont envoyées pour spécifier soit l’endroit où il devrait aller, soit la force qu’il devrait appliquer. Ces deux méthodes permettant de contrôler un robot ont malheureusement de sérieuses limitations :
- Une commande en position consiste à appliquer des couples sur les moteurs jusqu’à ce que la position voulue soit atteinte, quitte à appliquer des forces très élevées. Cela ne fonctionne donc que si la position peut être atteinte, car dans le cas contraire le robot pourrait forcer de toutes ses forces et endommager quelque chose, lui-même, voire quelqu’un !
- De façon similaire, une commande en force consiste à appliquer une force sur l’environnement. Cela peut avoir des effets imprévisibles si par exemple l’objet sur lequel les forces doivent être appliquées n’est pas présent : les efforts appliqués par les moteurs feront accélérer le robot qui pourra potentiellement atteindre des vitesses élevées et dangereuses.
Comme illustré sur la Figure 1, les problèmes dont nous parlons sont plutôt banals pour nous les humains : prendre un fruit, écrire avec un crayon, pousser ou tirer, rien de très impressionnant. Mais comment se fait-il que des problèmes apparemment aussi triviaux soient si complexes pour un robot ? La publication que nous étudions répond à cette question : les êtres vivants ont une astuce pour résoudre ces problèmes et encore mieux, c’est une astuce qu’un robot peut émuler.

Mais d’abord, c’est quoi une impédance mécanique ?
Commençons par définir la notion d’impédance mécanique, communément notée ![]() , qui caractérise la relation entre une force appliquée sur un système mécanique et sa vitesse [*]. L’impédance nous dit comment un objet va s’opposer au mouvement et permet donc de connaître la force qu’il va falloir appliquer pour le déplacer. Prenons le cas de trois composants classiques en mécanique : le ressort, l’amortisseur et la masse. Le plus simple est l’amortisseur, car son impédance se traduit par une force qui s’oppose linéairement à la vitesse, avec un coefficient de proportionnalité
, qui caractérise la relation entre une force appliquée sur un système mécanique et sa vitesse [*]. L’impédance nous dit comment un objet va s’opposer au mouvement et permet donc de connaître la force qu’il va falloir appliquer pour le déplacer. Prenons le cas de trois composants classiques en mécanique : le ressort, l’amortisseur et la masse. Le plus simple est l’amortisseur, car son impédance se traduit par une force qui s’oppose linéairement à la vitesse, avec un coefficient de proportionnalité ![]() entre les deux. Le ressort va quant à lui s’opposer au déplacement par rapport à sa position de repos, celle vers laquelle le ressort revient tout seul. Enfin, une masse va s’opposer à son accélération.
entre les deux. Le ressort va quant à lui s’opposer au déplacement par rapport à sa position de repos, celle vers laquelle le ressort revient tout seul. Enfin, une masse va s’opposer à son accélération.
Pour rendre ces notions plus concrètes, écrivons les relations pour des situations où nous voudrions déplacer un objet avec notre main. La force appliquée sur l’objet par la main est notée ![]() et la position, vitesse et accélération de l’objet sont respectivement notées
et la position, vitesse et accélération de l’objet sont respectivement notées ![]() ,
, ![]() et
et ![]() :
:
| Élément mécanique | Amortisseur | Ressort | Masse |
| Illustration | 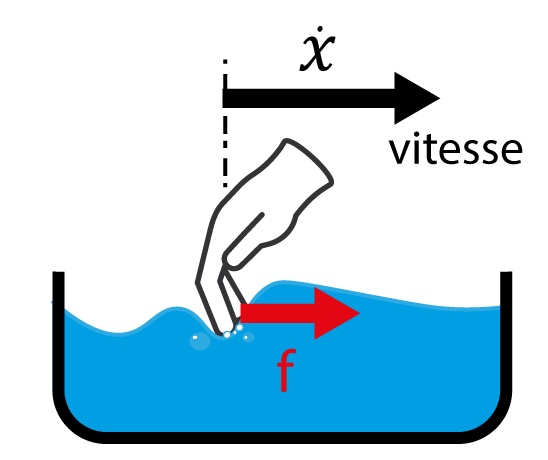 | 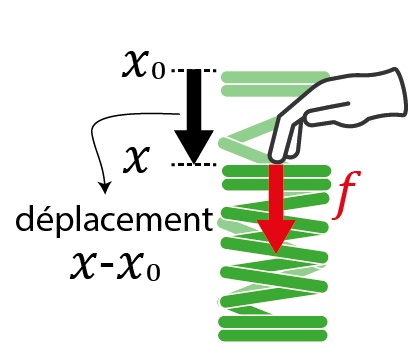 | 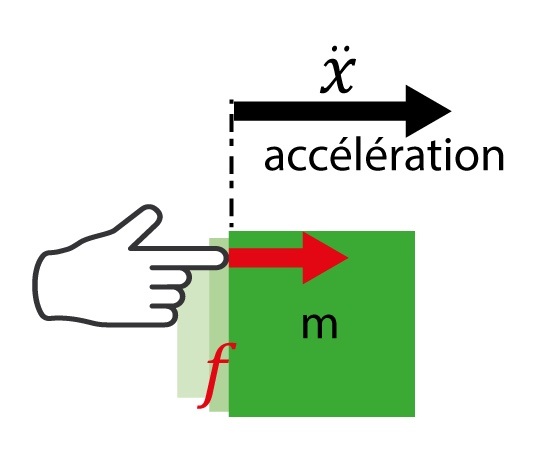 |
| Relation donnée par l’impédance mécanique |
De nombreux objets ont une impédance mécanique qui peut être grossièrement modélisée par un assemblage de ressorts, de masses et d’amortisseurs. Ceci est une analogie, c’est-à-dire une représentation simplifiée qui consiste à remplacer un système complexe par un autre plus simple qui a un comportement similaire. Par exemple, pour étudier le comportement d’une voiture sur une route chaotique, il est courant de représenter la voiture par une masse et de l’associer en série avec la suspension, représentée par l’association d’un ressort et d’un amortisseur en parallèle. Les valeurs de ![]() ,
, ![]() et
et ![]() peuvent alors être ajustées pour que notre modèle simplifié se comporte autant que possible comme la voiture. Dans la suite, nous utiliserons un modèle composé d’une masse, d’un ressort et d’un amortisseur (voir Figure 2) pour modéliser un comportement mécanique générique.
peuvent alors être ajustées pour que notre modèle simplifié se comporte autant que possible comme la voiture. Dans la suite, nous utiliserons un modèle composé d’une masse, d’un ressort et d’un amortisseur (voir Figure 2) pour modéliser un comportement mécanique générique.
Les humains, experts malgré eux de l’impédance mécanique
Comme suggéré dans l’introduction, la manière avec laquelle les humains manipulent des objets est une source d’inspiration pour résoudre certains problèmes en robotique. Il se trouve que nous nous comportons généralement comme une impédance mécanique quand nous interagissons avec notre environnement, même si c’est souvent inconscient. Notre posture et notre tension musculaire permettent de régler le comportement mécanique de notre corps pour absorber des chocs (ex : amortir une chute comme illustré sur la Figure 3), pour être plus souple (ex : pour écrire) ou à l’inverse pour devenir très rigide (ex : pour donner un coup de poing).

Principe de la commande en impédance (simplification en 1D)
La commande en impédance va alors consister à contrôler l’interaction mécanique entre le robot et son environnement de telle façon que si vous poussez le robot, il se comportera comme une impédance mécanique choisie à l’avance. L’impédance visée est alors celle d’un système composé d’un ressort, d’un amortisseur et d’une masse ; et les paramètres des trois composants pourront être ajustés afin de donner au système le comportement souhaité (Figure 4). Ce n’est donc plus seulement la force appliquée par un robot ou sa position que nous souhaitons contrôler, mais bien la relation entre les deux. Un exemple d’une telle relation pourrait être « plus on déplace le robot par rapport à une position de référence, plus la force appliquée par le robot augmente », ce qui serait modélisé par un ressort, ou bien « plus le robot se déplace vite, plus il va tenter de ralentir », ce qui est modélisé par un amortisseur. Pour revenir aux problèmes mentionnés dans l’introduction, cela permet d’adapter l’impédance mécanique du robot telle qu’elle peut être perçue par l’extérieur. Par exemple, pour être rigide (quitte à appliquer des forces élevées) il suffit de choisir une raideur élevée, mais pour être flexible (et ainsi limiter les forces) il va falloir choisir une raideur faible.
 |
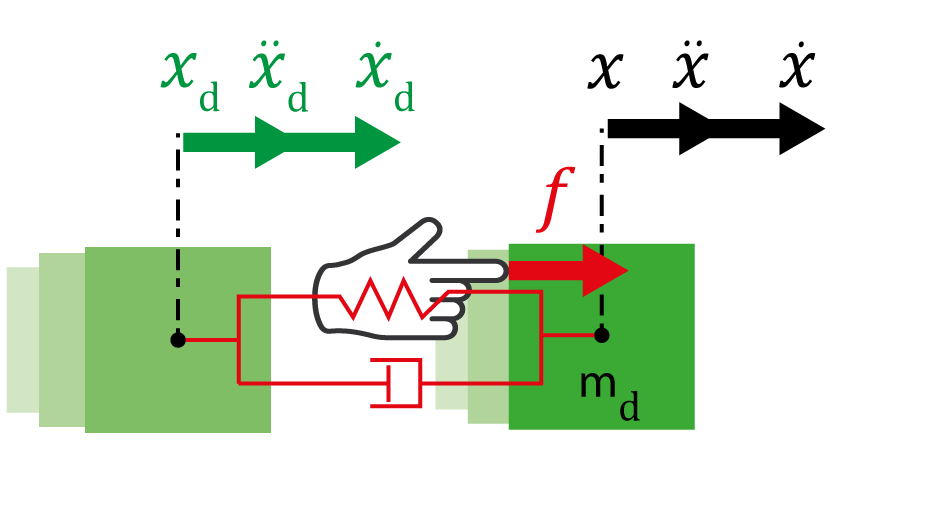
La force et la vitesse d’un système ne peuvent pas être simultanément contrôlées, donc pour imposer le comportement du robot il faut observer l’un et contrôler l’autre. Le robot va alors observer comment l’environnement l’oblige à se déplacer, puis appliquera des forces en conséquence : il se comportera donc bien comme une impédance mécanique, d’où le nom de la méthode. Dans la pratique, le robot doit non seulement s’adapter à l’environnement, mais doit également exécuter une tâche, c’est-à-dire se déplacer : il serait dommage que les robots ne puissent qu’être utilisés comme lampes de chevet de luxe… Nous ajoutons donc la vitesse et l’accélération désirées dans l’équation du comportement mécanique visé (voir Figure 5). Par « désirées », il faut comprendre « si possible », c’est-à-dire dans le cas où aucune force extérieure n’est appliquée sur le robot.
 |
Maintenant, il ne reste plus qu’à imposer ce comportement à un vrai robot ! Choisissons d’abord un « robot » qui soit le plus simple possible : un moteur déplace une masse à l’aide d’un système pignon/crémaillère (Figure 6). Nous asservissons le moteur pour qu’il ait un couple ![]() en sortie [**], ce qui permet alors d’imposer la force
en sortie [**], ce qui permet alors d’imposer la force ![]() sur la crémaillère. Le modèle dynamique de notre système est simplement :
sur la crémaillère. Le modèle dynamique de notre système est simplement :
![]()
avec ![]() la force appliquée par l’environnement (disons que quelqu’un va pousser dessus). Il est aussi supposé ici que l’on peut mesurer, à l’aide de capteurs, la force
la force appliquée par l’environnement (disons que quelqu’un va pousser dessus). Il est aussi supposé ici que l’on peut mesurer, à l’aide de capteurs, la force ![]() appliquée par l’environnement et la position
appliquée par l’environnement et la position ![]() .
.
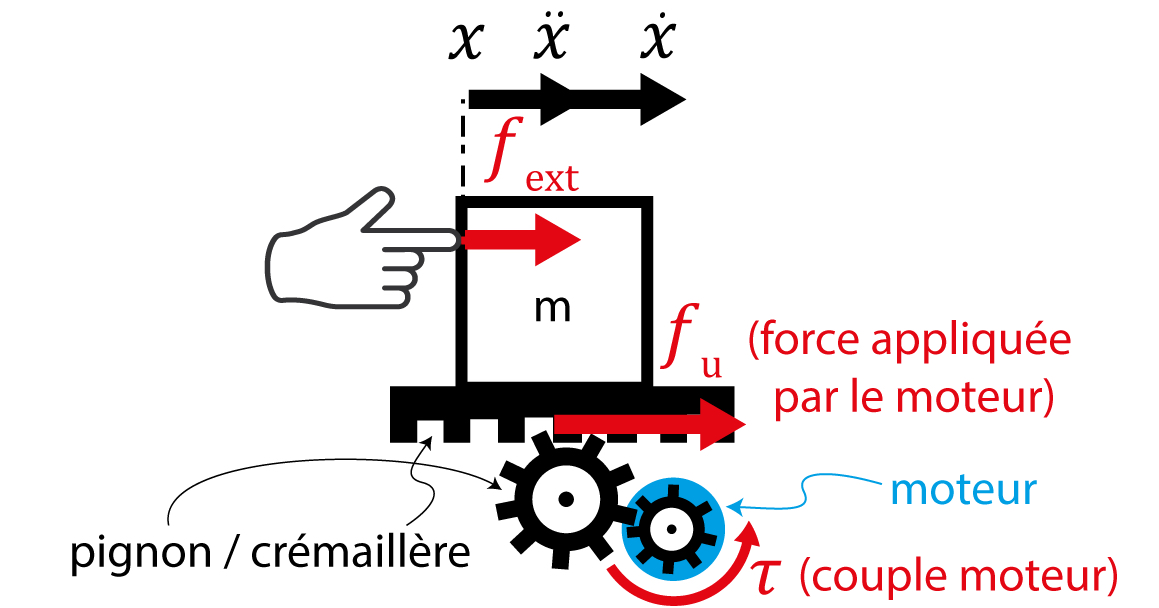
Bon je vous l’accorde, ce n’est pas l’exemple le plus excitant qui soit, mais c’est parfait pour expliquer le principe :
1. À partir du modèle dynamique, réécrire ![]() pour pouvoir commander l’accélération
pour pouvoir commander l’accélération ![]() du robot telle que
du robot telle que ![]() :
:
![]()
2. Définir le comportement mécanique désiré du robot sous la forme :
![]()
3. Calculer la commande en accélération ![]() et donc en force
et donc en force ![]() pour que le robot se comporte comme voulu (Figure 5) :
pour que le robot se comporte comme voulu (Figure 5) :
![]()
![]()
![]()
![]()
Et voilà, notre robot se comporte maintenant comme une masse accrochée à un ressort et amortie !
Applications & Limites
En règle générale, il faut adapter l’impédance mécanique (apparente) du robot suivant la situation. Si nous reprenons l’exemple de l’écriture à gauche de la Figure 1, il est raisonnable de dire que le crayon est très fragile. Il faudra donc que le geste du robot soit très souple pour réduire les forces et ne pas casser le crayon : la raideur choisie pour ![]() doit être très faible. Pour être sûr que le stylo touche la feuille, la position désirée
doit être très faible. Pour être sûr que le stylo touche la feuille, la position désirée ![]() envoyée au robot devra être située légèrement sous la surface de la feuille. Même si la table n’est pas exactement de la hauteur prévue, les forces d’interaction resteront faibles et le robot pourra faire autant de gribouillis qu’il le souhaite, sans casser le crayon.
envoyée au robot devra être située légèrement sous la surface de la feuille. Même si la table n’est pas exactement de la hauteur prévue, les forces d’interaction resteront faibles et le robot pourra faire autant de gribouillis qu’il le souhaite, sans casser le crayon.
Si nous fabriquons notre petit robot 1D (Figure 6) puis implémentons la commande en impédance, il se comportera un peu comme celui-ci. Le « grand moment » de cette vidéo est peut-être à environ 1 minute : l’impédance est réglée de façon à pouvoir déplacer le robot avec une chips sans la casser. Pour des robots plus compliqués, le principe reste le même, mais avec des matrices et vecteurs dans les équations car la translation et l’orientation du robot se font en 3D. Le résultat est parfois impressionnant vu qu’on ne s’attend pas à ce qu’un robot qui pèse 30, 50, 100 voire 200 kg soit aussi flexible quand nous le poussons. Voici deux exemples en vidéo avec un robot de la marque Kuka et l’autre de Franka Emika où le comportement du robot est bien visible.
Bien sûr, comme toute technique ou méthode, le contrôle par impédance n’est pas une solution miracle qui peut résoudre tous les problèmes. Les limites sont d’ailleurs discutées dans la partie III de la publication et il est important d’également les mentionner ici. La commande en impédance permet de moduler le comportement mécanique du robot, mais le prix à payer est que ni la force appliquée ni la position ne peuvent être imposées précisément. C’est donc un compromis entre précision et délicatesse : pour être précis il faut être très très rigide alors que pour être délicat, il faut être très souple…
Ce compromis est tout de même très intéressant, d’où le succès de cette technique depuis presque 40 ans (ces travaux datent de 1985) et le fait qu’elle soit toujours d’actualité. Aujourd’hui plus que jamais, les robots interagissent avec les humains au quotidien :
- les exosquelettes pour permettre à des personnes de (re)marcher ;
- les voitures autonomes ou même l’assistance à la direction dans les voitures pour nous aider à conduire ;
- les robots qui réalisent des tâches près des humains, par exemple les robots chirurgicaux ;
- peut-être dans le futur, des robots à la maison pour faire le ménage ou la cuisine ;
- etc.
Dans toutes ces situations, le fait que des humains soient présents rend le contrôle de l’interaction mécanique primordial. En plus des questions de sécurité, il faut prendre en compte des contraintes d’ergonomie et autres afin que l’utilisateur et la machine puissent collaborer efficacement. De fait, beaucoup de questions font toujours l’objet de recherche, par exemple pour apprendre automatiquement quel comportement mécanique est adapté pour exécuter une tâche ou pour adapter l’impédance mécanique au cours du temps.
Pour conclure, la commande par impédance est une technique très utile qui complémente bien les commandes classiques en force ou en position. Elle permet à des robots qui sont par nature lourds et rigides de paraître légers et souples, ce qui, comme nous l’avons vu, est parfois très important. Ce type de commande est également une brique de base pour de nombreuses applications où l’interaction mécanique doit être maîtrisée, comme celles où les robots doivent interagir avec nous.
Pour aller plus loin :
Si vous souhaitez obtenir des détails sur comment le contrôle en impédance est implémenté en général, je vous invite à visionner cette vidéo (en anglais) qui explique bien le raisonnement. Bien que le principe soit identique, les maths deviennent un peu plus corsées.
[*] En toute rigueur, l’impédance est notée ![]() où le terme «
où le terme « ![]() » représente une fréquence. Si vous vous demandez ce que ça vient faire ici, imaginez que vous êtes dans une piscine sur un vélo aquatique : si vous ne pédalez pas vite, l’eau ne résiste pas ou peu, mais en pédalant plus vite ça devient vite très épuisant !
» représente une fréquence. Si vous vous demandez ce que ça vient faire ici, imaginez que vous êtes dans une piscine sur un vélo aquatique : si vous ne pédalez pas vite, l’eau ne résiste pas ou peu, mais en pédalant plus vite ça devient vite très épuisant !
[**] Dans la pratique, la commande se fait au niveau des moteurs donc au lieu de commander la force ![]() nous allons commander le couple
nous allons commander le couple ![]() .
.