Écriture : Astrid Thébault-Guiochon
Relecture scientifique : Sandrine Cremona et Agathe Pralus-Durand
Relecture de forme : Christine Duthoit et Aurélien Schwob
Temps de lecture : environ 12 minutes.
Thématiques : Apprentissage et Neurosciences Cognitives (Sciences Cognitives)
Publication originale : Girard C., et al., Nurturing the Mathematical Brain: Home Numeracy Practices Are Associated With Children’s Neural Responses to Arabic Numerals. Psychological Science, 2022. DOI : 10.1177/09567976211034498. Accès libre sur HAL (pdf).

Et si les mathématiques pouvaient aussi être une affaire de famille ? C’est ce que les neurosciences semblent nous dire. Une équipe de recherche lyonnaise a utilisé l’imagerie cérébrale pour étudier le cerveau d’enfants. Elle s’est concentrée sur une petite zone du cerveau traitant les chiffres. Les neuroscientifiques ont trouvé qu’on pouvait développer les compétences en mathématiques des enfants grâce à certaines activités à la maison, mais pas n’importe lesquelles…
Avez-vous déjà entendu parler de « la bosse des maths » ? C’est cette idée selon laquelle on pourrait naître avec une prédisposition pour les mathématiques. Les enfants « bossus » deviendraient de vrais génies du calcul, tandis que les autres se perdraient dans les abysses arithmétiques. La réalité ? Tout le monde possède cette « bosse », elle se développe juste différemment selon les personnes. Mais on peut l’entraîner à la maison.
Pendant l’Antiquité, Aristote [*] imagine que l’intellect réside dans le cœur. Au Moyen-Âge, on pense que le cerveau est parcouru par quatre liquides qui déterminent le tempérament (Claude Galien [**]) aussi fortement que l’on croit que c’est le Soleil qui tourne autour de la Terre. Et au XIXe, Franz Gall [***] introduit la phrénologie, théorie selon laquelle le caractère d’une personne réside dans la forme, et plus particulièrement dans les bosses, de son crâne.
Il propose une carte des fonctions cérébrales et explique que la forme du crâne serait influencée par le développement du cerveau. On pourrait donc observer les traits de caractères d’une personne grâce à la localisation de ses bosses. On retrouverait par exemple la détermination en haut du crâne, l’amitié à l’arrière, la cupidité au centre, ou encore le calcul à l’avant, d’où la bosse des maths !
Bref, assez parlé d’Histoire, place aux calculs ! Pardon… aux neurosciences, et retour au présent. Depuis, cette théorie a été réfutée, le cerveau regroupe effectivement différentes aires cérébrales et fonctions cognitives, mais on ne peut les étudier en se basant sur la forme du crâne, donc plus de bosses à l’horizon !
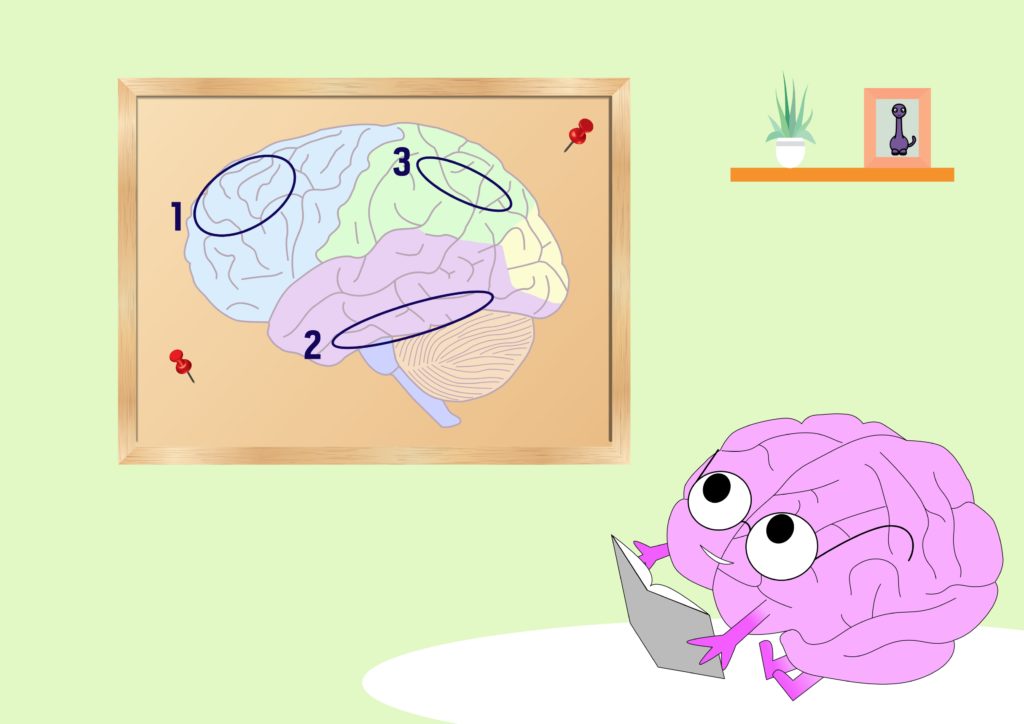
Effectivement, on sait dorénavant que les bosses du crâne ne donnent aucune information sur les habiletés cognitives et que ces dernières fonctionnent généralement en réseaux impliquant plusieurs aires au sein du cerveau. Il n’existe donc pas une aire allouée à une fonction cognitive particulière mais la collaboration de plusieurs aires qui peuvent être impliquées dans différents réseaux. On ne peut alors identifier une aire spécifique dédiée aux mathématiques qui nous permettrait de comprendre les différences de compétences numériques entre les enfants. En revanche, une étude utilisant l’imagerie par résonance magnétique fonctionnelle met en évidence un « réseau des mathématiques » impliquant le cortex frontal dorsal, le cortex inférotemporal ainsi que les sillons intrapariétaux (Figure 1) [1]. On possèderait donc plusieurs « bosses » des mathématiques, situées respectivement à l’avant du cerveau (cortex frontal, support des fonctions telles que la résolution de problèmes et la planification), sur les côtés latéraux inférieurs (bas du cortex temporal, impliqué dans le traitement visuel) et sur la partie supérieure du cerveau (le long du lobe pariétal, zone notamment impliquée dans l’attention et le contrôle de certains mouvements). Ce réseau impliquerait donc plusieurs aires cérébrales collaborant pour traiter et manipuler les mathématiques.
Maintenant que l’on sait qu’il existe des bosses aires des mathématiques, il s’agit de comprendre comment elles se développent, et surtout, de savoir si on peut les gonfler à bloc pour devenir un·e boss des maths…
Un réseau de bosses d’aires
Effectivement, on a bien souvent l’impression que les mathématiques ne sont qu’à la portée d’un petit cercle de personnes nées pour les comprendre. Elles deviennent alors rapidement la source de difficultés à l’école. Il existe des disparités entre les enfants au niveau de l’apprentissage des mathématiques, qui peuvent impacter le reste de leur scolarité ainsi que les perspectives de poursuite d’études en post-bac, et même les métiers. Ces enjeux motivent les cerveaux des scientifiques (et des parents comme enseignant·es) à trouver la ou les sources de telles différences, et comment y remédier. On les attribue souvent à des facteurs liés à la pédagogie et à l’accès à l’éducation [2]. Toutefois, on sait dorénavant que ces disparités existent avant même l’entrée en maternelle : les compétences en mathématiques peuvent donc être influencées en dehors de l’école [3].
Et ce n’est pas que le cas des mathématiques. Par exemple, de nombreux·ses scientifiques ont observé des liens entre les compétences linguistiques des enfants et la catégorie socio-professionnelle des parents [4]. On imagine alors observer un phénomène similaire pour les mathématiques. Toutefois, d’autres scientifiques ont mis en évidence que les fonctions langagières et les fonctions cognitives liées aux mathématiques se distinguaient dans le cerveau : les énoncés mathématiques (algèbre, analyse, topologie, géométrie) n’activent pas les aires liées au langage comme une histoire le ferait [1]. Il existe donc des régions qui traitent spécifiquement ce qui est lié aux mathématiques, y compris des simples faits (sans traitement numérique ou calcul) [5]. Ainsi, si on reste dans l’image des bosses, lire la phrase « les chameaux ont des bosses » génèrerait un traitement dans des zones cérébrales différentes que celles interprétant l’énoncé mathématique « la fonction gaussienne se dessine comme une grosse bosse ».
Ces zones qui s’activent lorsqu’on lit des énoncés mathématiques ou qu’on effectue des calculs sont localisées dans des régions différentes mais impliquées dans le même réseau. Le cerveau n’est donc pas divisé en une multitude de « bosses » chacune allouée à une fonction particulière, mais plutôt en régions spécialisées dans une ou plusieurs fonctions, qui collaborent avec d’autres régions cérébrales plus ou moins éloignées. Ces zones présentent donc une sensibilité aux mathématiques, mais pas n’importe lesquelles. Par exemple, les opérateurs logiques élémentaires (comme le fameux « ![]() » qui se lit « pour tout
» qui se lit « pour tout ![]() ») ne constituent pas des concepts assez « puissants » pour activer ces zones, tandis que les nombres ou encore l’énoncé « la fonction gaussienne se dessine comme une grosse bosse » le sont [6].
») ne constituent pas des concepts assez « puissants » pour activer ces zones, tandis que les nombres ou encore l’énoncé « la fonction gaussienne se dessine comme une grosse bosse » le sont [6].
La bosse L’aire des chiffres dans le cerveau
Dans notre cas, l’équipe de recherche s’est concentrée sur une seule bosse aire : le sillon intrapariétal (Figure 1). Il serait impliqué dans le traitement des nombres, donc une zone d’étude pertinente notamment quand on cherche à comprendre les différences de niveau en mathématiques chez les enfants en étudiant directement la zone qui automatise leur traitement [7]. Par ailleurs, le sillon intrapariétal s’activerait quel que soit le domaine mathématique et la difficulté [6]. L’équipe de recherche a exploré les relations entre la pratique des mathématiques à la maison, l’activité cérébrale notamment dans le sillon intrapariétal et le niveau des enfants en mathématiques, en émettant plusieurs hypothèses. La première étant que la pratique des mathématiques influencerait l’activité cérébrale liée aux nombres dans le sillon intrapariétal ; la deuxième que cette activité serait liée au niveau arithmétique des enfants ; et la troisième que l’activité cérébrale liée aux nombres dans le sillon intrapariétal expliquerait la relation entre pratique à la maison et les compétences en mathématiques.
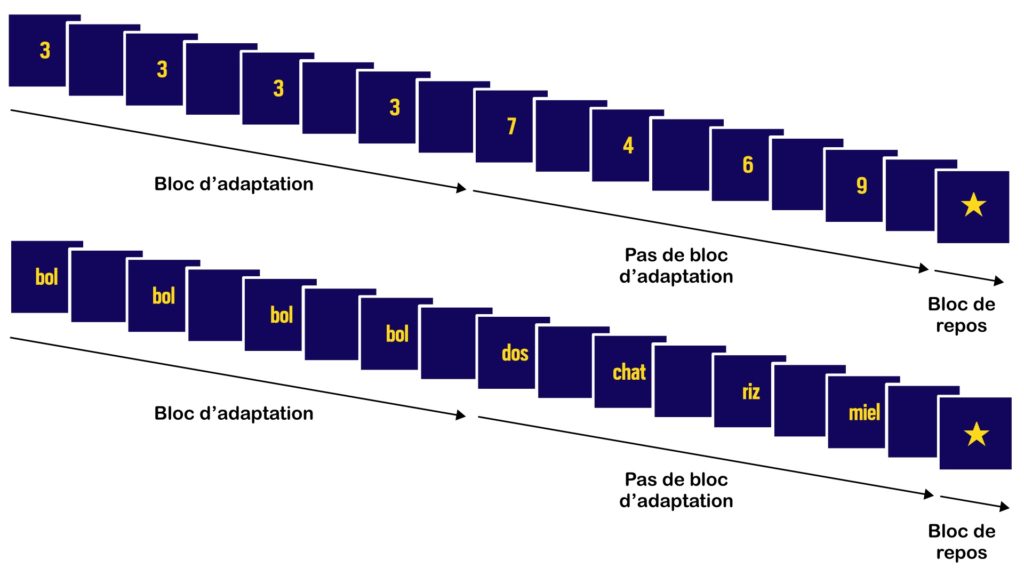
Dans cette optique, cette équipe a utilisé un appareil d’imagerie par résonance magnétique fonctionnelle (IRMf, [pour approfondir : voir note A]) pour observer l’activité cérébrale d’enfants de 8 ans observant des chiffres et des mots (situation contrôle permettant d’identifier ce qui est spécifique au traitement cérébral des chiffres). Les scientifiques souhaitaient mesurer le degré de spécialisation cérébrale à traiter les chiffres. Pour cela, les enfants ont observé un écran qui alterne la diffusion du même chiffre 8 fois de suite (pour étudier le phénomène d’adaptation) et 8 chiffres différents (pas d’adaptation). On leur présentait aussi soit 8 fois le même mot d’affilée (adaptation), soit 8 mots différents (pas d’adaptation) pour vérifier l’existence d’une activité cérébrale spécifique pour les chiffres différente de celle des lettres (Figure 2).
Cette tâche offre la possibilité d’étudier la familiarité des enfants (notamment au niveau de leur sillon intrapariétal) avec les chiffres afin de la comparer à leurs compétences en mathématiques. Enfin, pour mesurer ces compétences et les comparer à ce qu’il se passe dans le cerveau, on leur a fait passer ce qu’on appelle un test de fluence en arithmétique afin d’estimer le niveau en mathématiques des enfants en utilisant un ensemble de problèmes arithmétiques à résoudre en un temps limité [pour approfondir : voir note B].
L’imagerie cérébrale a permis de confirmer que le sillon intrapariétal était activé lors de la présentation des chiffres, comme les études antérieures le suggéraient. L’équipe de recherche a aussi observé que le phénomène d’adaptation numérique était plus important dans le sillon intrapariétal des enfants ayant obtenu un score élevé au test de fluence en arithmétique. En d’autres termes, les enfants ayant les meilleurs scores en arithmétiques automatisent davantage le traitement des chiffres. Les enfants présentant une meilleure habituation aux chiffres possèdent un meilleur niveau en arithmétique que les enfants avec une habituation cérébrale moindre aux chiffres. À partir de ce résultat, on observe un lien entre les compétences en mathématiques et l’activité cérébrale dans le sillon intrapariétal.
Entraîner sa bosse son aire des maths à la maison
Maintenant qu’on pense que le niveau en mathématiques, et notamment la sensibilité aux chiffres, serait associé à l’activité cérébrale dans le sillon intrapariétal, la possibilité de développer cette zone se questionne. L’équipe de recherche a ainsi demandé aux parents des enfants de remplir un questionnaire quant aux activités à la maison. Il leur a notamment été demandé de préciser à quelles activités familiales impliquant des nombres les enfants prenaient part. Elles ont ensuite été classées selon leur complexité (basique ou avancée) ainsi que leur approche (formelle ou informelle) [pour approfondir : voir note C].
Ces informations concernant la pratique formelle ou non des mathématiques à la maison ont permis aux chercheuses et chercheurs de les comparer au traitement des chiffres dans le sillon intrapariétal et au niveau en mathématiques. Elles ont aussi servi à étudier si le traitement plus ou moins efficace des chiffres dans le sillon intrapariétal était susceptible d’expliquer la relation entre pratiques d’activités impliquant des nombres à la maison et niveau des enfants en mathématiques. En outre, le questionnaire révèle des différences importantes dans la fréquence des activités liées aux mathématiques à la maison. Certains enfants s’exercent tous les jours tant en lisant l’heure ou la température qu’en réalisant des opérations et en comptant jusqu’à 1 000, tandis que d’autres manipulent les chiffres de temps en temps, sans directement réaliser des calculs à la maison, par exemple en pesant des aliments au supermarché ou en cuisinant.
L’équipe de recherche a observé un lien entre la pratique des mathématiques à la maison et l’activité cérébrale dans le sillon intrapariétal [pour approfondir : voir note A]. Plus les enfants pratiquent des activités mathématiques à la maison, plus la présentation répétée du même chiffre entraîne une diminution de l’adaptation au niveau du sillon intrapariétal. Autrement dit, le cerveau se spécialise à traiter plus efficacement les chiffres. La manipulation des chiffres à la maison (en plus de la pratique scolaire) permettrait de développer une meilleure sensibilité aux chiffres dans cette région. Plus précisément, les scientifiques ont remarqué que plus les enfants prennent part à des activités mathématiques formelles et complexes comme compter jusqu’à 1 000 et effectuer des opérations sur des nombres à deux chiffres, plus ces enfants automatisent le traitement des chiffres dans leur sillon intrapariétal.
En outre, l’équipe de recherche a remarqué que l’activité cérébrale dans ce sillon en présence de chiffres était associée au niveau en mathématiques des enfants. En d’autres termes, leurs compétences arithmétiques seraient liées à la sensibilité aux chiffres dans le sillon intrapariétal. Comme on l’a vu, cette sensibilité se développe par la pratique : plus on effectue des activités liées aux chiffres, plus on automatise leur traitement. Quand le cerveau automatise une tâche, ici le traitement des chiffres, cela lui permet de faciliter la réalisation d’opérations de calcul mental. Dans ce cas, cela pourrait offrir la possibilité aux enfants d’être plus à l’aise en arithmétique et de faire des calculs plus poussés ou même de les faire plus rapidement, donc d’avoir un meilleur niveau en mathématiques.
Plus on calcule à domicile, plus ça devient facile
La relation entre la pratique d’activités liées aux chiffres à la maison et le niveau en mathématiques des enfants serait donc médiée par l’activité cérébrale en présence de chiffres dans le sillon intrapariétal. La pratique des mathématiques augmenterait la sensibilité aux chiffres dans le cerveau qui influencerait les compétences des enfants en mathématiques (Figure 3).
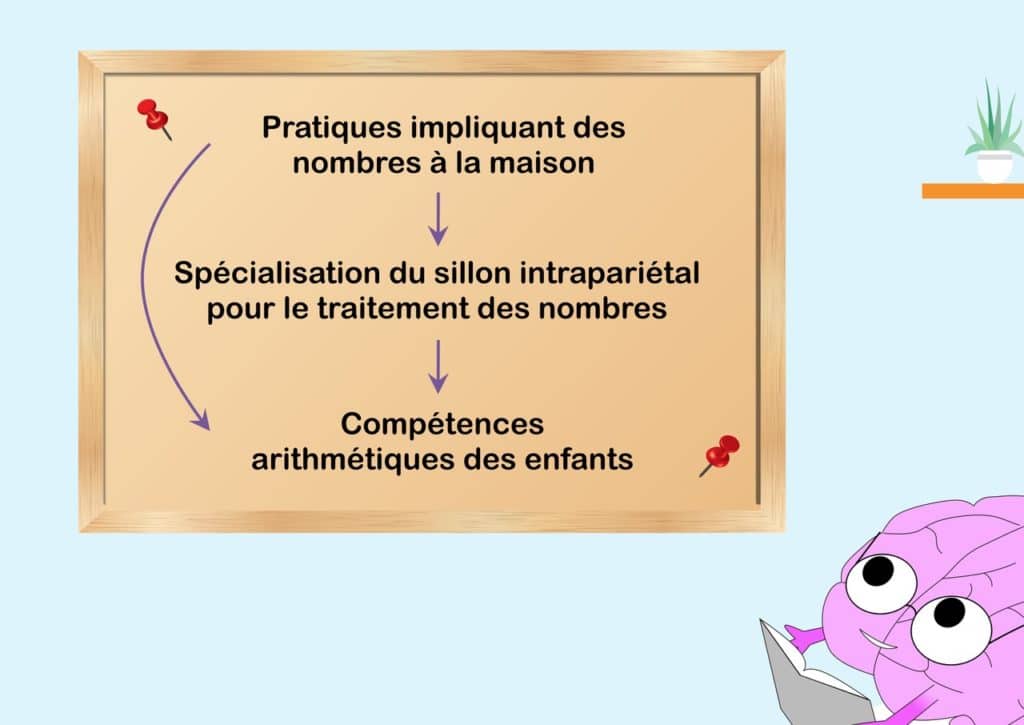
Toutefois, ce phénomène s’observerait uniquement lorsqu’il s’agit d’activités formelles (d’apprentissage) et complexes pour l’âge des enfants : lire et écrire les nombres jusqu’à 1 000 et effectuer des opérations sur des nombres à deux chiffres (10 et plus). On pourrait donc améliorer le traitement des chiffres et donc le niveau en mathématiques des enfants en les faisant pratiquer, même en dehors de l’école. Bien sûr, il ne faut pas oublier de nuancer ces résultats en les complétant par d’autres études (notamment une étude qui met en évidence d’autres explications concernant les différences de niveau en mathématiques des enfants [8]), et en réitérant l’expérience en suivant plus d’enfants et sur toute leur scolarité, même avant l’entrée à l’école. Effectivement, tout comme l’intérêt de la lecture à la maison, manipuler les chiffres à travers des activités familiales se montre primordial et bénéfique pour les enfants. Alors, même à la maison, on peut développer sa bosse zone des maths !
Éléments pour approfondir
Afin d’étudier l’adaptation cérébrale — c’est-à-dire une diminution des activations cérébrales — à force de répétition d’un même stimulus, l’équipe de recherche a comparé l’activité cérébrale en présence de chiffres identiques à l’activité cérébrale avec des chiffres différents. Autrement dit, les activations cérébrales relatives à la répétition du même stimulus (8 fois le même chiffre) ont été soustraites des activations cérébrales associées à la présentation de différents stimuli (8 chiffres différents).
Ces activités ont été mesurées grâce à l’imagerie par IRMf qui permet de visualiser l’activité cérébrale en mesurant les changements d’oxygénation dans le cerveau (plus une zone cérébrale est active, plus elle consomme d’oxygène). Ces mesures obtenues, il est possible d’étudier le cerveau découpé en cubes de quelques millimètres de côté, appelés voxels, l’équivalent 3D des pixels (2D). Les voxels sont l’unité de mesure pour calculer les différences d’activation cérébrale dans les différentes conditions expérimentales.
Dans le cas présent, l’équipe souhaitait étudier les relations entre l’activité cérébrale, la pratique des mathématiques à la maison et les compétences arithmétiques des enfants. Pour ce faire, l’équipe de recherche a utilisé un outil de modélisation (le MEPM) conçu pour analyser les données de neuroimagerie.
Le MEPM propose de tester les différentes relations possibles entre les données. Pour chaque voxel (le fameux petit cube de cerveau), il modélise les trois relations possibles (Figure 3) :
- Pratiques à la maison → Activité cérébrale
- Activité cérébrale → Compétences en mathématiques
- Pratiques à la maison → Activité cérébrale → Compétences en mathématiques
Le MEPM teste si chaque voxel s’active significativement pour une relation. Autrement dit, il estime l’activité cérébrale (en comparant la tâche avec des chiffres différents qui sert de témoin et celle avec des chiffres répétés qui est le but de l’étude) dans chaque unité du cerveau (le voxel) et vérifie si elle est statistiquement assez forte (significative) pour être impliquée dans l’une des relations.
Pour évaluer leurs compétences en arithmétique, les enfants ont passé un test de fluence arithmétique, c’est-à-dire un test mesurant l’efficacité et la rapidité à traiter et manipuler les chiffres. Les enfants disposaient de 3 minutes pour répondre à un grand nombre de problèmes arithmétiques. Il s’agissait d’effectuer de simples calculs, à savoir des additions, soustractions et multiplications sur des nombres allant de 0 à 10. Il fallait donner le plus de bonnes réponses le plus rapidement possible. En fonction du nombre de réponses correctes, un score a été établi pour estimer l’aisance en arithmétique des enfants. En bref, le score au test de fluence reflète à quel point les enfants ont automatisé les mathématiques, tout comme à force de lire on a automatisé la lecture : lettre par lettre, puis syllabe par syllabe, plus on pratique plus on automatise la lecture jusqu’à reconnaître les mots, voire des expressions entières, instantanément.
Les parents ont rempli un questionnaire concernant les pratiques à la maison dans différents domaines dont les mathématiques. Sur les 36 pratiques arithmétiques à la maison, 17 étaient considérées comme informelles et les 19 autres comme formelles. Les pratiques informelles constituent des activités quotidiennes comme lire l’heure, compter de l’argent, peser des aliments, etc. Les pratiques formelles, elles, sont directement liées à l’idée de transmission et d’apprentissage : compter, écrire des nombres, réaliser des opérations, etc. Elles se divisent en deux catégories selon leur complexité pour un enfant de 8 ans : les pratiques formelles basiques concernent la lecture et l’écriture des nombres jusqu’à 100 ainsi que les opérations sur des chiffres, tandis que les pratiques formelles plus avancées font référence à la lecture et à l’écriture des nombres jusqu’à 1 000 et des opérations sur des nombres à deux chiffres (supérieurs à 9). Les parents ont aussi renseigné la fréquence de ces pratiques (une fois par jour, plusieurs fois par semaine, une fois par semaine, quelques fois dans le mois).
[*] Philosophe de l’Antiquité Grecque s’étant intéressé à un large panel de domaines, notamment la biologie et la physique (384-322 av. J-C).
[**] Médecin de l’Antiquité grecque ayant largement influencé la médecine, tout comme Hippocrate (d’où le fameux serment prononcé par les médecins en devenir) (129-201).
[***] Médecin et neuroanatomiste allemand, fondateur de la phrénologie et précurseur des neurosciences cognitives avec ses travaux de dissection (1758-1828). Carte de la phrénologie ici.
[1] Amalric M., et al., Origins of the brain networks for advanced mathematics in expert mathematicians. PNAS, 2016. DOI : 10.1073/pnas.1603205113. [Publication scientifique]
[2] Sokolowski H.M., et al., Understanding the effects of education through the lens of biology. npj Science of Learning, 2017. DOI : 10.1038/s41539-018-0032-y. [Publication scientifique]
[3] Duncan G.J., et al., School readiness and later achievement. Developmental Psychology, 2007. DOI : 10.1037/0012-1649.43.6.1428. [Publication scientifique]
[4] Farah M.J., The neuroscience of socioeconomic status: Correlates, causes, and consequences. Neuron, 2017. DOI : 10.1016/j.neuron.2017.08.034. [Publication scientifique]
[5] Amalric M., et al., Cortical circuits for mathematical knowledge: evidence for a major subdivision within the brain’s semantic networks. Philosophical transactions of the Royal Society B, 2017. DOI : 10.1098/rstb.2016.0515. [Publication scientifique]
[6] Amalric M., et al., A distinct cortical network for mathematical knowledge in the human brain. NeuroImage, 2019. DOI : 10.1016/j.neuroimage.2019.01.001. [Publication scientifique]
[7] Bugden S., et al., When Your Brain Cannot Do 2 + 2: A Case of Developmental Dyscalculia. Frontiers for Young Minds, 2014. DOI : 10.3389/frym.2014.00008. [Publication scientifique]
[8] Bakker, M., et al., Longitudinal pathways of numerical abilities in preschool: Cognitive and environmental correlates and relation to primary school mathematics achievement, Developmental psychology, 2022. DOI : 10.1037/dev0001491. [Publication scientifique]