Comment montrer que « la mutation précède la sélection » avec une poignée de virus et de bactéries : l’expérience de Luria et Delbrück

Chargement de l'article...

Écriture : Irène Tanneur
Relecture scientifique : Maud Billaud et Bastien Mallein
Relecture de forme : Guillaume Witz et Carlotta Figliola

Temps de lecture : environ 10 minutes.
Thématiques : Évolution, Génétique et Microbiologie (Biologie)

Publication originale : Luria S. E. & Delbrück M., Mutations of Bacteria from Virus Sensitivity to Virus Resistance. Genetics, 1943.

Photographie en microscopie électronique à transmission de bactériophages à la surface d’une bactérie. Grossissement d’environ x200 000. Crédit : Dr Graham Beards/Wikimedia Commons/CC BY-SA 3.0.

En 1943, les connaissances sur l’hérédité ou la sélection et en particulier leurs bases génétiques n’en sont qu’à leurs balbutiements. Des questions fondamentales restent ouvertes, par exemple : comment les caractères héréditaires apparaissent-ils ? Est-ce que la pression de sélection joue un rôle dans l’hérédité ? À l’aide d’expériences de sélection sur des bactéries infectées par des phages (des virus bactériens), deux chercheurs, Max Delbrück et Salvador Luria, vont répondre à ces questions alors que le mécanisme biologique sous-jacent — les mutations de l’ADN — est encore inconnu.

L’étude des « virus bactériens » soulève des questions

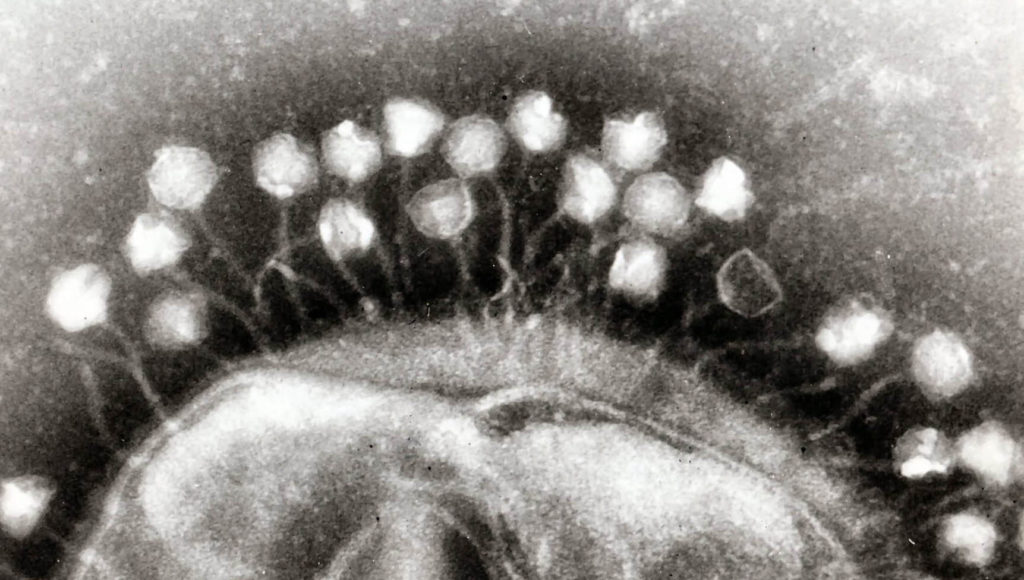
Les virus sont des organismes contenant des acides nucléiques, les longues molécules portant l’information génétique (comme l’ADN). Ils doivent obligatoirement infecter une cellule pour reproduire leur matériel génétique. Si le mot « virus » peut vous évoquer des maladies humaines, par exemple la grippe dont le virus infecte des cellules humaines, les bactéries aussi peuvent aussi être infectées par des virus. Ceux-ci, découverts au début du XX^e siècle, sont appelés bactériophages ou tout simplement phages.

En microbiologie, une technique de routine parmi les plus simples et les plus essentielles est la culture des bactéries. Elle peut se faire dans un liquide ou sur un solide. Dans le premier cas, il s’agit de placer quelques bactéries dans un liquide contenant tous les nutriments nécessaires à leur croissance ; souvent, cette technique est effectuée en tube à essai. Les bactéries vont utiliser les nutriments pour croître et se diviser, donnant naissance à de nouvelles bactéries et ainsi de suite. Plus il y a de bactéries dans une culture, plus elle va être turbide, c’est-à-dire trouble (Figure 1). Puisque la quantité de nutriments pour les bactéries est limitée, une culture ne peut contenir qu’un nombre limité de bactéries : quand ce nombre est atteint, on dit que la culture est à saturation.

**Figure 1. Deux flasques contenant une culture bactérienne après une nuit d’incubation (à gauche) et du milieu sans bactéries (à droite).** On observe à gauche que la culture est devenue trouble. Crédit : Joseph Elsbernd/flickr/CC BY 2.0.

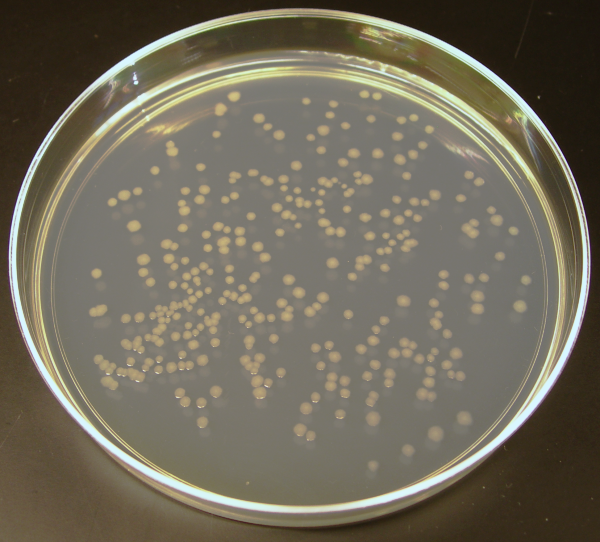
Ajoutez un peu de gélifiant à cette nourriture à bactéries, versez le tout dans une boîte, et vous pouvez les faire pousser, c’est-à-dire les faire croître sur un milieu solide. Cela permet, lorsque le nombre de cellules est assez petit, de séparer spatialement les bactéries les unes des autres et d’observer des clones : des ensemble de bactéries toutes issues d’un même ancêtre, facilement repérables sur le milieu solide (Figure 2).

**Figure 2.** **Des bactéries de l’espèce *Escherichia coli* sur un milieu solide.** Chaque point blanc isolé correspond à une colonie bactérienne : des bactéries toutes issues d’un même ancêtre. Compter ces points revient à connaître le nombre initial de bactéries placées sur le milieu de culture solide.

Maintenant, si vous placez des phages dans une culture liquide de bactéries à saturation, vous observerez que la culture s’éclaircit. C’est parce que les phages ont lysé les bactéries : en d’autres termes, ils les ont tuées. Néanmoins, après quelque temps, la culture redevient turbide ! Cela signifie que certaines bactéries n’ont pas été lysées par les phages et ont recommencé à croître et à se diviser dans le milieu de culture. On dit alors que ces bactéries sont résistantes au phage, et qu’elles ont été sélectionnées : contrairement aux autres bactéries, elles sont adaptées au milieu contenant des phages. La sélection est le processus grâce auquel les organismes les plus aptes à survivre dans un environnement vont y devenir prédominants.

Mais quand ces bactéries deviennent-elles résistantes au phage ? Avant ou après l’ajout des phages à la culture ? En 1943, certains scientifiques pensent que la résistance héréditaire arrive grâce à l’action du phage, et donc qu’aucune bactérie ne peut être résistante avant l’ajout du phage. Pour d’autres, la résistance est apparue par hasard avant cet ajout. Le débat se divise donc entre deux hypothèses. Selon la première, la résistance des bactéries est acquise en réponse à la présence du phage ; selon la seconde, une mutation — une modification de la séquence d’ADN de la bactérie qui empêche le phage de l’infecter ou de la lyser — apparaît tout d’abord, et cette mutation précèderait la sélection.

Ces questions ne concernent pas que les bactéries et les phages, mais s’inscrivent dans un débat plus large sur l’évolution et le rôle de la sélection : est-ce que, soumis à une sélection, les êtres vivants changent pour s’adapter à cette sélection, ou bien est-ce que la sélection ne fait que mettre en avant les êtres qui y étaient déjà adaptés auparavant, en éliminant les autres ?

La grande loterie des mutations

Luria et Delbrück prennent pour point de départ les observations effectuées sur les bactéries et les phages pour tenter de trancher. Ils nomment la première théorie l’hypothèse d’immunité héréditaire acquise, et la seconde l’hypothèse mutationnelle. Pour vérifier laquelle décrit le mieux les expériences menées avec des bactéries et des phages, ils s’interrogent sur le nombre de bactéries résistantes attendues dans une culture infectée par des phages selon chacune des deux hypothèses.

Selon l’hypothèse d’immunité acquise, avant l’infection, certaines bactéries seraient capables de résister au phage, mais pas de transmettre cette résistance à leur descendance ; c’est l’interaction avec le phage qui rendrait la résistance au phage héréditaire, c’est-à-dire transmissible à toutes les bactéries issues de cette bactérie « mère ». Donc, dans ce premier cas, si l’on fait pousser des bactéries dans plusieurs cultures séparées, les proportions de bactéries résistantes suite à une infection devraient être semblables d’une culture à l’autre.

Selon l’hypothèse mutationnelle en revanche, la bactérie a une faible chance de devenir spontanément et par hasard résistante, et elle transmettra cette résistance à toute sa descendance, y compris en l’absence de contact avec le phage. Là, en fonction du moment où a eu lieu la mutation, le nombre de mutants d’une culture à l’autre devrait donc être très variable. Si elle a lieu tôt dans la culture — ce qui est peu probable car il y a alors peu de bactéries — il y aura un grand nombre de bactéries résistantes car chaque bactérie se divise en 2 en transmettant la mutation. À l’inverse, si elle se produit vers la fin de la culture, lorsqu’il y a un grand nombre de bactéries — ce qui est davantage probable —, il y aura peu de bactéries résistantes car elles n’auront pas beaucoup de temps pour se diviser. Donc, dans ce second cas, si l’on considère plusieurs cultures séparées, on devrait avoir :

un petit nombre de cultures avec un nombre de bactéries résistantes au virus bien supérieur à la moyenne, si la mutation est apparue tôt ;
un grand nombre de cultures avec un petit nombre de bactéries résistantes, si la mutation est apparue plus tard.

L’article compare cette situation à celle rencontrée avec les machines à sous : très souvent, au final vous récoltez moins d’argent que vous n’en avez misé ; mais exceptionnellement, le gain remporté sera très élevé : c’est le jackpot ! Les mutations, c’est l’argent gagné !

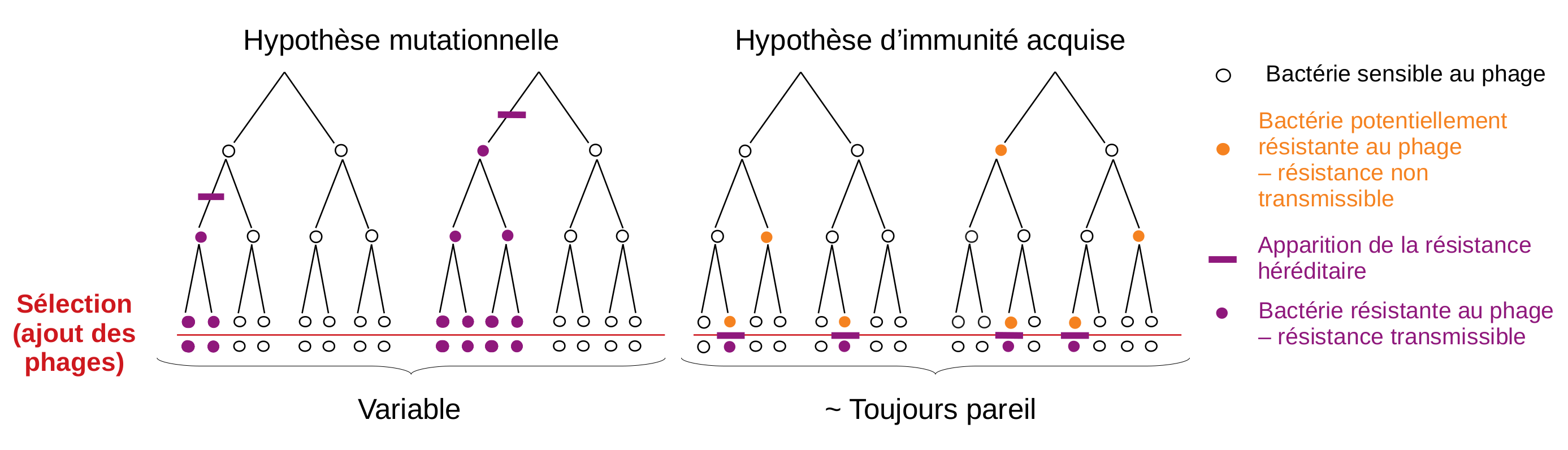
Ce modèle de la « machine à sous » montre que si l’hypothèse mutationnelle est vérifiée, la variabilité du nombre de bactéries résistantes entre les cultures devrait donc être beaucoup plus grande que si c’est l’hypothèse d’immunité héréditaire acquise qui est vérifiée. Le raisonnement des chercheurs leur permet alors de prédire l’ampleur de la variabilité du nombre de bactéries attendues en fonction de chaque hypothèse (Figure 3). Ne reste plus qu’à expérimenter pour le tester.

Légende : point violet "Bactérie résistance au phage, résistance transmissible" ; point orange "Bactérie potentiellement résistance au phage, résistance non transmissible" ; trait violet "Apparition de la résistance héréditaire" ; point blanc "Bactérie sensible au phage".
Arbre de gauche "Hypothèse mutationnelle". Arbre avec des points blancs. Après un trait violet, tous les points des bactéries filles sont violets aussi. Après sélection (ajout des phages), rien en change. Arbre de gauche "Hypothèse d'immunité acquise". Arbre avec des points blancs. Quelques points oranges aléatoires. Après sélection (ajout des phages), un triat violet apparaît puis un point violet remplace un point orange. — **Figure 3. Représentation schématique de l’apparition des mutations pendant la division cellulaire, ici sur trois générations, en fonction de l’hypothèse considérée.** Chaque arbre représente une expérience différente. Chaque nœud de l’arbre représente une bactérie. La division d’une bactérie est représentée comme un nouvel embranchement créant deux bactéries-filles. Selon l’*hypothèse mutationnelle*, le nombre de mutants devrait être variable d’une culture à l’autre, en fonction du moment d’apparition de la mutation. Selon l’*hypothèse d’immunité acquise*, le nombre de mutants devrait être stable entre les cultures.

C’est l’heure de jouer !

Concrètement, les chercheurs ont utilisé la bactérie Escherichia coli (E. coli) — déjà bien connue et caractérisée [1] — et le phage α, qui sera plus tard renommé phage T1 par Delbrück lui-même.

Les volumes et milieux de culture peuvent varier d’une expérience à l’autre. Aussi, pour s’assurer que les expériences sont robustes, des cultures bactériennes sont réalisées en double dans les mêmes conditions et le même jour : ce sont des cultures parallèles. À plusieurs reprises, les auteurs de la publication ont laissé croître entre cinq et cent cultures parallèles d’E. coli jusqu’à saturation. Ils ont ensuite étalé la culture sur un milieu de culture solide, en présence d’une grande quantité de phages. 24 ou 48 heures après étalement, ils comptent les clones maintenant visibles à l’œil nu sur le milieu, et qui sont tous issus de bactéries résistantes au phage (Figure 4). Le nombre de clones correspond donc au nombre de bactéries résistantes au moment de l’ajout des phages.

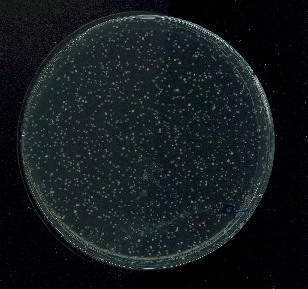
**Figure 4. Des bactéries mises en contact avec des phages, sur milieu solide**. Sur 10 à 100 millions de bactéries, quelques centaines se sont révélées résistantes : les clones issus de ces bactéries sont visibles sur le milieu. Les autres ont été lysées, et ne sont donc pas visibles. Expérience réalisée dans le laboratoire *Bactériophages de bactéries Gram-positives* de l’I2BC (CNRS).

À partir du nombre de bactéries résistantes au phage présentes sur chaque boîte, ils peuvent calculer la moyenne et la variabilité du nombre de bactéries sur une expérience. Surprise : la variabilité des résultats observée est bien plus grande que celle qu’ils avaient prédite pour l’hypothèse mutationnelle !

Pour eux, cette importante variation du nombre de mutants va à l’encontre de l’hypothèse d’immunité acquise. Ces résultats confirment donc l’hypothèse mutationnelle.

À travers ces expériences, Luria et Delbrück montrent que la résistance de leurs bactéries à ce phage est une mutation héritable, dont l’apparition et la transmission sont indépendantes de l’action du phage lui-même.

Pour la première fois, une estimation du taux de mutation

À la fin de leur article, Luria et Delbrück appliquent deux méthodes différentes pour estimer le taux de mutation, c’est-à-dire la probabilité qu’une bactérie E. coli devienne résistante au virus T1

Ils trouvent un taux de mutation moyen d’environ 10^-8 mutations par cellule et par génération, avec peu de variations d’une expérience à l’autre. Il y a donc environ une chance sur 40 millions pour que, lors d’une division cellulaire, la cellule-fille devienne résistante au phage. Leurs expériences montrent également que le milieu et le volume de culture, ainsi que le nombre de cultures parallèles au sein d’une même expérience n’apporte pas de différence significative au taux de mutation.

L’héritage de Luria et Delbrück

Outre une démonstration que « la mutation précède la sélection » et non l’inverse, Luria et Delbrück ont aussi développé un protocole expérimental qui a fait date. Le protocole qu’ils ont mis en œuvre, appelé par la suite le test de fluctuation, est encore utilisé de nos jours pour estimer le taux de mutation d’un organisme, même si de nouveaux modèles mathématiques permettent de l’estimer de manière plus fiable.

D’autres pressions de sélection peuvent aussi être appliquées. Par exemple, les bactéries peuvent également acquérir des mutations qui leur permettent de résister à un antibiotique. Il est alors possible d’effectuer le test de fluctuation en étalant les bactéries non pas sur du milieu contenant des phages, mais sur du milieu contenant des antibiotiques.

L’avènement des techniques de séquençage du génome complet — qui permettent de lire l’intégralité de l’information génétique d’un organisme — a également fait naître de nouveaux protocoles pour estimer des taux de mutation.

Les mécanismes qui se produisent dans la bactérie et qui conduisent à la résistance au phage T1 ont également été élucidés. Les mutations se produisent sur des gènes codant pour des protéines placées sur la membrane cellulaire — à la frontière entre l’extérieur et l’intérieur de la cellule — qui sont bien pratiques pour importer, par exemple, du fer dans la cellule, mais servent également de récepteur à différents phages, dont le phage T1.

[1] Blount Z. D., The unexhausted potential of E. coli. eLife, 2015. DOI : 10.7554/eLife.05826. [Publication scientifique]

Publié le 20/07/2020

Irène Tanneur/Papier-Mâché/CC BY-NC-SA 4.0 2020

Texte et images, à l’exception des images soumises à droits d’auteurs différents : voir au cas par cas en légende.

Écriture : Irène Tanneur
Relecture scientifique : Maud Billaud et Bastien Mallein
Relecture de forme : Guillaume Witz

Temps de lecture : environ 16 minutes.
Thématiques : Évolution, Génétique et Microbiologie (Biologie)

Publication originale : Luria S. E. & Delbrück M., Mutations of Bacteria from Virus Sensitivity to Virus Resistance. Genetics, 1943.

Les « virus bactériens » soulèvent des questions

Dans les années 1910, deux chercheurs découvrent de manière indépendante et presque simultanée l’existence de virus qui infectent et tuent spécifiquement certaines bactéries. Il s’agit de Frederick Twort, au Royaume-Uni[1], et de Félix d’Hérelle, en France. C’est ce dernier qui appelle ces virus des bactériophages, qui sont aujourd’hui plus simplement appelés phages. Lorsque des phages sont mis en contact avec des bactéries, cela conduit à la lyse d’une majorité d’entre elles. Pourtant, une fraction des bactéries est résistante : elles survivent au contact des phages et poursuivent leur croissance. Cette résistance est en général spécifique : en d’autres termes, une bactérie résistante à un type de phage n’est pas nécessairement résistante à un autre type de phage. Une question fondamentale se pose alors aux chercheurs de l’époque : à quel moment le caractère de résistance à un phage devient-il héréditaire ? Avant ou après l’ajout des phages à la culture ? Certains, dont Félix d’Hérelle, pensent que la résistance devient héréditaire grâce à l’action du phage. D’autres soutiennent que la résistance héréditaire est apparue avant cet ajout, et que les bactéries résistantes sont donc restées en vie parce qu’elles ou l’une de leurs ancêtres avaient, par hasard, acquis la résistance. Le débat se divise donc entre une hypothèse plutôt lamarckienne d’une transmission des caractères acquis en réponse à une condition à laquelle l’organisme aurait été soumis, et une autre darwinienne selon laquelle la mutation précède la sélection.

Les deux hypothèses mènent à des prédictions différentes sur la probabilité qu’une bactérie devienne résistante. Mais comment mesurer ces probabilités expérimentalement pour vérifier ces hypothèses ? Il faut un moyen de faire croître des bactéries, de les infecter avec des phages et finalement de « compter » les bactéries survivantes.

Expérimenter avec des bactéries : comment les voir ?

En microbiologie, une des techniques les plus simples et les plus essentielles est la culture des bactéries. Elle peut se faire dans un liquide ou sur un solide. Dans le premier cas, il s’agit de placer quelques bactéries dans un liquide contenant des nutriments permettant la croissance des bactéries : souvent, cette technique est effectuée en tube à essai. Les bactéries vont utiliser les nutriments pour croître et se diviser, donnant naissance à de nouvelles bactéries, et ainsi de suite. Plus il y a de bactéries dans une culture, plus elle va être turbide, c’est-à-dire trouble (Figure 1). Puisque la quantité de nutriments pour les bactéries est limitée, une culture ne peut contenir qu’un nombre limité de bactéries : quand ce nombre est atteint, on dit que la culture est à saturation.

Ajoutez un peu de gélifiant à cette nourriture à bactéries, versez le tout dans une boîte, et vous obtenez un milieu solide à la surface duquel faire pousser des bactéries. Pour ce faire, une petite quantité de milieu de culture contenant des bactéries à faible densité est réparti sur la surface. Dans l’idéal, toutes les bactéries sur la surface sont à bonne distance de leurs voisines et vont se multiplier jusqu’à former des colonies individuelles : des ensembles de bactéries toutes issues d’un même ancêtre, et facilement repérables sur le milieu solide à l’œil nu (Figure 2). Nous obtenons alors un moyen de compter les bactéries !

L’expérience menée par les chercheurs va donc consister à faire croître les bactéries en milieu liquide puis de faire croître les bactéries ainsi infectées sur un milieu solide comprenant des phages pour finalement pouvoir compter les survivantes.

Modéliser la grande loterie des mutations

Luria et Delbrück prennent pour point de départ les protocoles expérimentaux déjà réalisés sur les bactéries et les phages et les observations qui en découlent pour tenter de trancher entre l’hypothèse de la transmission des caractères acquis (lamarckienne) et celle selon laquelle la mutation précède la sélection (darwinienne). Ils nomment la première supposition l’hypothèse d’immunité héréditaire acquise (acquired hereditary immunity), et la seconde l’hypothèse mutationnelle (mutation hypothesis). Pour vérifier laquelle décrit le mieux les expériences menées avec des bactéries et des phages, ils s’interrogent sur le nombre de bactéries résistantes attendues selon chacune des deux hypothèses.

L’hypothèse d’immunité acquise comprend, en elle-même, deux possibilités :

soit les bactéries résistantes sont prédisposées à résister au phage par une mutation, et l’interaction avec lui ne fera que rendre ce caractère héréditaire ;
soit la prédisposition des bactéries est due à un certain nombre de critères physiologiques (âge, taille) qui peuvent être aléatoires, mais encore une fois, c’est la mise en contact avec le phage qui immunise toute leur descendance.

Selon cette hypothèse, dans les deux cas, à un instant t, la probabilité qu’une bactérie soit résistante sera identique dans chaque culture.

Selon l’hypothèse mutationnelle en revanche, la bactérie a une faible chance de devenir spontanément résistante par hasard, et elle transmettra ce caractère à toute sa descendance, y compris en l’absence de contact avec le phage.

Ces différences fondamentales entre les deux hypothèses sur l’origine et la transmission héréditaire de la résistance ont des conséquences sur le nombre de bactéries résistantes qui sont attendues lors des infections par les phages comme celles décrites plus haut. En effet, dans le cas de l’hypothèse d’immunité acquise, il y a une petite probabilité pour chaque bactérie de survivre à l’attaque, et elle est la même pour chaque bactérie. Si tel est le cas, alors le nombre de bactéries sera un échantillon aléatoire de la culture, distribué selon une loi de Poisson (Figure 3).

Aux variations près, une proportion constante de bactéries résistantes serait attendue dans chaque culture. La loi de Poisson a une propriété intéressante : son espérance — le nombre moyen théorique d’évènements attendus si l’expérience pouvait être répétée un très grand nombre de fois — est égale à sa variance. La variance est le paramètre de dispersion des données, égal au carré des écarts à la moyenne pour chaque donnée prélevée. Plus les données sont éloignées de la moyenne, c’est-à-dire plus elles sont variables, plus la variance sera élevée. Gardez cela en tête, nous y reviendrons plus tard.

4 histogrammes, P(X=k) en fonction de k, avec k de 0 à 10. La distribution varie en fonction de la valeur de lambda. Pour lambda = 0,5 et 1, pic puis décroissance des valeurs puis plateau. Pour lambda = 2, ça augmente puis pic pour k=2 et ça décroît. Pour lambda = 5, pic au milieu du graphique. — **Figure 3.** **Distributions de Poisson.** La probabilité d’obtenir un nombre d’évènements k est représentée, en fonction du nombre moyen d’événements attendus 𝜆. Dans l’hypothèse d’immunité acquise, 𝜆 correspond au nombre moyen de bactéries résistantes attendues à la fin de l’expérience ; la distribution donne, en fonction de 𝜆, la probabilité d’avoir k bactéries résistantes.

Considérons maintenant l’hypothèse mutationnelle. Ici, chaque bactérie a une probabilité finie, et infime, de passer par mutation de « sensible au virus » à « résistante au virus » par unité de temps. Les chercheurs nomment cette variable le taux de mutation. Dans un petit intervalle de temps donné, le nombre de mutations apparaissant serait donc ce taux de mutation, multiplié par le nombre de bactéries en culture pendant ce petit intervalle et par la durée même de l’intervalle de temps. Sur une culture complète, cela correspond à :

$m = a\tau(N_{\mathrm{t}} -N_0)$

(*)

avec
$m$ : le nombre de mutations ;
$a$ : le taux de mutation ;
$\tau$ : le temps caractéristique de la croissance exponentielle, égal au temps de division des bactéries divisé par ln(2) ;
$N_0$ et $N_{\mathrm{t}}$ : respectivement le nombre de bactéries initial et final.

La différence $N_{\mathrm{t}} -N_0$ correspond par ailleurs au nombre de divisions bactériennes, chacune de ces divisions faisant naître une nouvelle bactérie. C’est pendant cette division que les mutations peuvent apparaître.Enfin, le taux de mutation est considéré constant tout au long de la croissance des bactéries dans la culture.

Si m est le nombre moyen de mutations par culture, alors le nombre de mutations de chaque culture est distribué selon une loi de Poisson de paramètre $m$ .

À partir de là, facile ! Il suffit de faire pousser les bactéries, de les mettre en présence de phages, et de compter le nombre de bactéries résistantes pour avoir le taux de mutation, non ?

Pas si vite ! En effet, suivant l’hypothèse mutationnelle, les bactéries résistantes présentes au moment de l’ajout des phages ne sont pas seulement les bactéries qui ont muté, mais également leur descendance.

Il y a donc deux facteurs d’augmentation du nombre de mutants résistants : l’apparition de nouvelles mutations, et la croissance des mutants déjà résistants. Le nombre de mutants peut donc être différent entre deux cultures qui ont pourtant connu le même nombre de mutations, en fonction du moment où la mutation est apparue.

Néanmoins, comme les mutations sont des évènements aléatoires, il est possible que la mutation conférant la résistance apparaisse très tôt, et donc qu’il y ait un grand nombre de mutants en fin de culture suite aux divisions successives de la bactérie résistante. Mais cet évènement est peu probable, puisqu’il y a au début peu de bactéries dans la culture. À l’inverse, il est plus probable que les mutations — s’il y en a — apparaissent au cours des dernières générations. Dans ce cas, il y aura peu de mutants à la fin de la culture.

En prenant tous ces paramètres en compte, si l’on considère plusieurs cultures, selon l’hypothèse mutationnelle, on devrait avoir :

un petit nombre de cultures avec un nombre de bactéries résistantes au virus bien supérieur à la moyenne lorsque la mutation apparaît tôt ;
un grand nombre de cultures avec un petit nombre de bactéries résistantes lorsque la mutation apparaît au cours des dernières générations.

L’article compare cette situation à celle rencontrée avec les machines à sous : très souvent, le gain est très inférieur à ce que vous avez misé ; mais très rarement, le gain sera exceptionnel : c’est le jackpot !

Cette hypothèse peut être mathématiquement résumée en disant que si le nombre de mutations est distribué selon une loi de Poisson, le nombre de mutants n lui ne l’est pas. En prenant ces deux facteurs en compte, les auteurs calculent le nombre moyen de bactéries résistantes attendues en fonction du temps, du taux de mutation et du nombre de bactéries. Ils prennent pour hypothèse que les mutants résistants ont le même taux de croissance que les bactéries sensibles, autrement dit, qu’ils se divisent à la même vitesse.

Si l’hypothèse mutationnelle est vérifiée, la variance (c’est-à-dire la variation du nombre de bactéries résistantes entre toutes les cultures) devrait donc être beaucoup plus grande que si c’est l’hypothèse d’immunité héréditaire acquise qui est vérifiée. En effet, pour l’hypothèse d’immunité héréditaire acquise, le nombre de bactéries résistantes est approximativement le même d’une culture à l’autre au moment de l’infection, et l’interaction avec le phage ne fera que rendre la résistance héréditaire. Le nombre de résistants par culture, dans ce cas, devrait être globalement homogène entre toutes les cultures (Figure 4).

C’est l’heure de jouer !

Les chercheurs ont utilisé pour cela la bactérie Escherichia coli — déjà bien connue et caractérisée [2] — et le phage $\alpha$ , qui sera plus tard renommé phage T1 par Delbrück lui-même.

Ils vérifient tout d’abord le caractère stable de la résistance en s’assurant que les bactéries résistantes ne peuvent pas être réinfectées par le même phage. Puis, à plusieurs reprises, ils laissent croître entre cinq et cent cultures parallèles d’Escherichia coli jusqu’à saturation, avant d’étaler tout ou partie de la culture sur un milieu de culture solide, en présence d’une grande quantité de phages. Deux milieux et deux volumes de culture sont testés, ils varient donc d’une expérience à l’autre. Pour s’assurer que les expériences sont robustes, des cultures bactériennes sont réalisées en double dans les mêmes conditions et le même jour : c’est l’intérêt des cultures parallèles. Ils prennent soin d’observer, au microscope, que la lyse des bactéries mises en contact avec les phages a lieu très rapidement. Les bactéries n’ont donc pas le temps de se diviser avant d’être lysées, de sorte que les colonies qui apparaissent sont bien issues de bactéries déjà résistantes au moment de l’étalement. Les comptages de bactéries résistantes sont effectuées 24 ou 48 heures après les étalements, lorsque les colonies sont visibles à l’œil nu (Figure 5).

**Figure 5. Des bactéries mises en contact avec des phages, sur milieu solide**. Sur 10 à 100 millions de bactéries, quelques centaines se sont révélées résistantes : les clones issus de ces bactéries sont visibles sur le milieu. Les autres ont été lysées, et ne sont donc pas visibles. Expérience réalisée dans le laboratoire *Bactériophages de bactéries Gram-positives* de l’I2BC (CNRS).

Pour chaque expérience — composée, donc, de plusieurs cultures — les chercheurs indiquent le nombre de bactéries résistantes et le nombre total final de bactéries par culture. À partir de là, ils calculent la moyenne, la variance et le ratio variance/moyenne du nombre de mutants par culture. Surprise : ce ratio est encore plus grand que celui qu’ils avaient prédit mathématiquement si l’hypothèse mutationnelle était vérifiée !

Notamment, il y a, dans beaucoup d’expériences, davantage de cultures comprenant plus de bactéries résistantes que ce qui avait été anticipé. Les chercheurs mettent en avant différentes hypothèses qui permettraient d’expliquer cette différence, remettant notamment en question leur modèle mathématique. Ils émettent également la supposition que le taux de mutation pourrait ne pas être constant tout au long de la culture, contrairement à l’un de leurs postulats de départ. Pour eux, cet important ratio variance/moyenne du nombre de mutants va à l’encontre de l’hypothèse d’immunité acquise. Ces résultats semblent donc être en faveur de l’hypothèse mutationnelle !

Pour la première fois, une estimation du taux de mutation

À la fin de leur article, Luria et Delbrück appliquent deux méthodes différentes pour estimer le taux de mutation — la probabilité qu’une bactérie Escherichia coli devienne résistante au virus T1 — avec leurs données.

Nous l’avons vu plus haut : le nombre de mutations par culture est considéré comme distribué selon une loi de Poisson, même si le nombre de mutants ne l’est pas. Néanmoins, la proportion de cultures dans laquelle il n’y a pas eu de mutations est égale à la proportion de cultures sans mutants ayant survécu à l’infection. Celle-ci peut donc être considérée comme un estimateur du terme zéro de la distribution de Poisson : soit la probabilité, connaissant le nombre de mutations moyen par culture, qu’il n’y ait pas de mutants dans une culture prise au hasard.

Ce terme, le $p_0$ est égal à $\mathrm{e}^{-m}$ , où $m$ est le nombre de mutations moyen. Cette estimation permet un calcul simple, mais nécessite que le design expérimental permette d’avoir des cultures sans mutants : ce n’est le cas que pour une seule des expériences de Luria et Delbrück.

À partir des données de cette expérience, ils estiment $m$ , et l’équation (voir formule (*)) les ramène au taux de mutation, qu’ils estiment être de 0,32.10^-8 mutation par cellule et par division. Autrement dit, selon ce calcul, il y a environ une chance sur 300 millions pour que, lors d’une division cellulaire, la cellule-fille devienne résistante au phage.

Une autre manière de calculer le taux de mutation leur est donnée par un modèle mathématique développé pour estimer la variance attendue du nombre de mutants par culture. Ce modèle leur a permis de trouver une méthode d’estimation du taux de mutation en fonction :

de la moyenne du nombre de mutants observés dans un ensemble de cultures semblables et lancées en parallèle ;
du nombre de cultures ;
du nombre final de bactéries dans les cultures.

Ici, toutes les expériences qu’ils rapportent peuvent être prises en compte. Ils trouvent alors un taux de mutation moyen de 2,45.10^-8 mutation par cellule et par division (soit une chance sur 40 millions environ), avec peu de variations d’une expérience à l’autre. Cela montre que le milieu de culture n’influe pas significativement sur le taux de mutation, alors même que le métabolisme et le temps de reproduction des bactéries varie entre les deux milieux utilisés. De même, le volume de culture ou le nombre de cultures parallèles au sein d’une même expérience n’apporte pas de différence significative au taux de mutation.

Néanmoins, ce taux de mutation moyen est près de dix fois supérieur au taux trouvé avec la méthode du $p_0$ : cela est dû aux cultures pour lesquelles le nombre de mutants est élevé, qui ne sont pas prises en compte dans la méthode du $p_0$ , mais qui augmentent significativement la moyenne du nombre de mutants observés sur laquelle est basée cette seconde méthode de calcul.

L’héritage de Luria et Delbrück

Outre une démonstration que « la mutation précède la sélection », Luria et Delbrück ont aussi développé un protocole expérimental qui a fait date. Le test de fluctuation est encore utilisé de nos jours pour estimer le taux de mutation d’un organisme, même si de nouveaux modèles mathématiques ont été développés pour relier d’une manière plus juste la distribution de mutants observés au nombre de mutations par culture et in fine au taux de mutation.

Par exemple, ces modèles permettent de prendre en compte des variations dans le nombre final de bactéries par culture ou un taux de croissance différent d’un organisme à un autre. Néanmoins, la méthode du $p_0$ est toujours employée, en particulier dans les estimations des taux de mutations des virus [3].

D’autres pressions de sélection peuvent également être appliquées : si Luria et Delbrück ont utilisé des phages, il est également possible, par exemple, d’utiliser une résistance à un antibiotique pour laquelle les mutations sont connues.

L’avènement des techniques de séquençage du génome complet, qui permettent de lire l’information génétique d’un organisme, a également fait naître de nouveaux protocoles pour l’estimation des taux de mutation.

Les mécanismes qui mènent à la résistance au phage T1 ont également été élucidés. Les gènes bactériens fhuA et tonB codent pour des protéines placées sur la membrane cellulaire — à la frontière entre l’extérieur et l’intérieur de la bactérie — qui sont bien pratiques pour importer du fer dans la bactérie… mais servent également de récepteur à différents phages, dont le phage T1 ! Une mutation sur l’un de ces gènes peut donc empêcher le phage de s’accrocher à la bactérie, en la rendant ainsi la rendre résistante.

[1] Twort F. W., An investigation on the nature of ultra-microscopic viruses. The Lancet, 1915. DOI : 10.1016/S0140-6736(01)20383-3. [Publication scientifique]

[2] Blount Z. D., The unexhausted potential of E. coli. eLife, 2015. DOI : 10.7554/eLife.05826. [Publication scientifique]

[3] Sanjuan R., et al., Viral Mutation Rates. Journal of Virology, 2010. DOI : 10.1128/JVI.00694-10. [Publication scientifique]

Publié le 20/07/2020

Irène Tanneur/Papier-Mâché/CC BY-NC-SA 4.0 2020

Texte et images, à l’exception des images soumises à droits d’auteurs différents : voir au cas par cas en légende.

La publication scientifique facile à digérer !