Voyage immobile au centre de la Terre : à la découverte du noyau de fer liquide

Chargement de l'article...

Écriture : Anaïs Kobsch
Relecture scientifique : Lambert Baraut-Guinet
Relecture de forme : Charlotte Remy et Éléonore Pérès

Temps de lecture : environ 11 minutes.
Thématiques : Minéralogie (Géologie)

Publication originale : Kuwayama Y., et al., Equation of State of Liquid Iron under Extreme Conditions, Physical Review Letters, 2020. DOI : 10.1103/PhysRevLett.124.165701
Accès libre sur HAL (pdf).

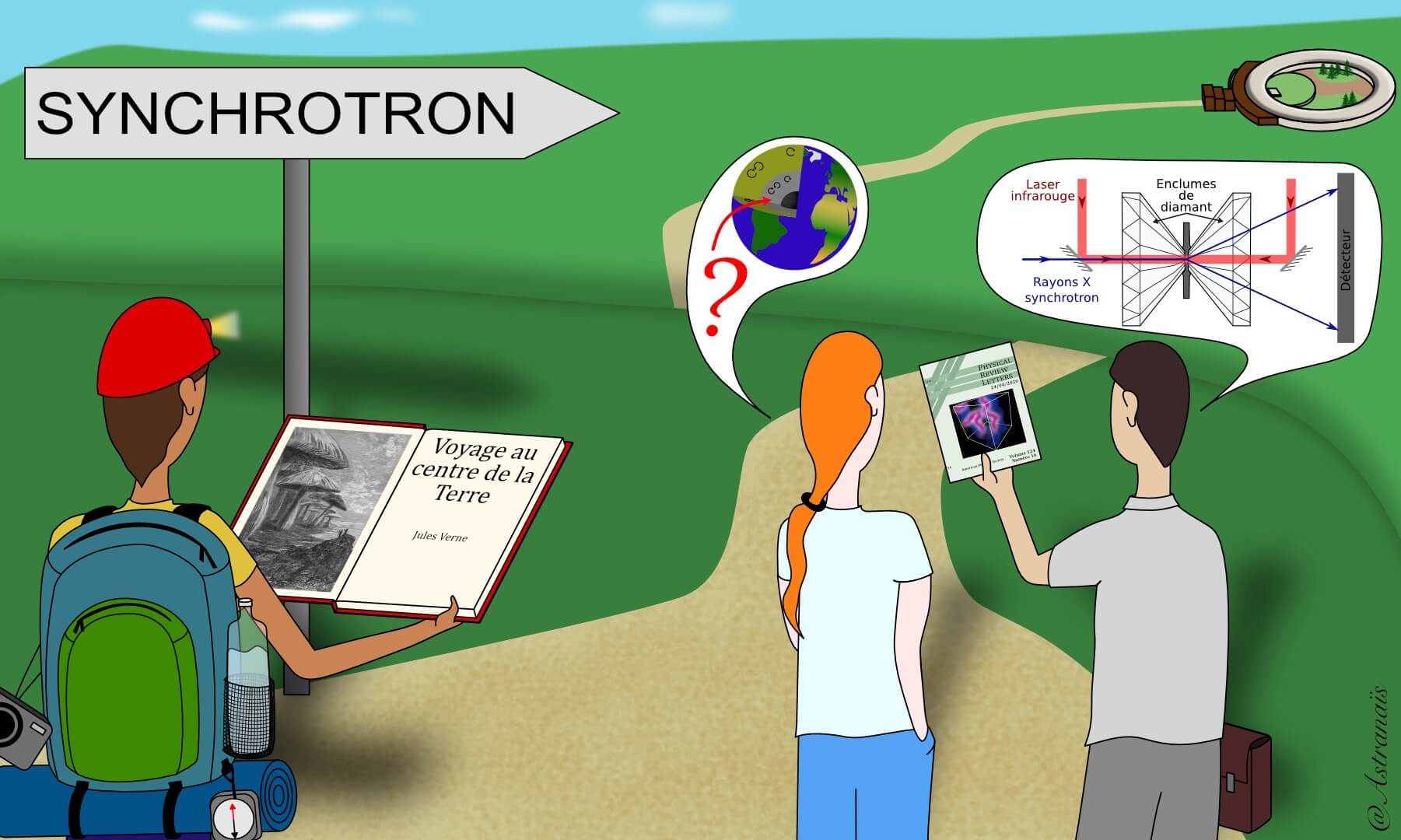
Dessin illustrant le trajet de deux personnes vers un synchrotron.

Nous savons qu’il y a, au centre de la Terre, une coquille sphérique de fer liquide autour de la graine de fer solide. Cette partie liquide du noyau de la Terre est capitale pour nous, car c’est là qu’est généré le champ magnétique terrestre. Il est donc tout naturel de vouloir en apprendre plus sur sa composition et ses propriétés physiques. Mais peut-on vraiment explorer le centre de la Terre sans avoir (ou presque) à bouger de son laboratoire ? La réponse est oui. Cet article vous montrera comment l’équipe de recherche a reproduit en laboratoire les conditions extrêmes proches de celles régnant au sommet du noyau terrestre.

Que découvrir dans ce voyage au centre de la Terre ?

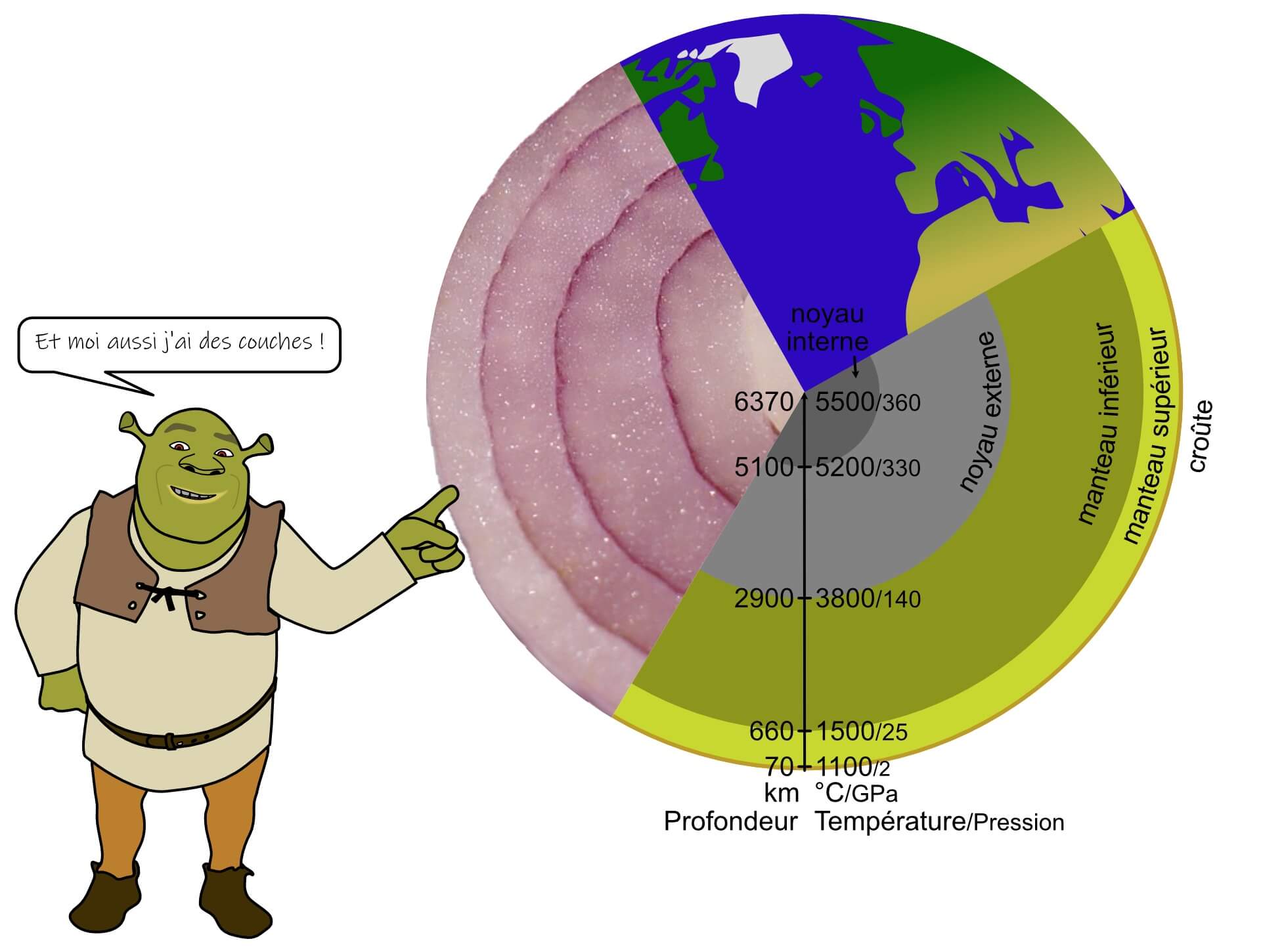
La Terre est un peu comme les oignons (ou les ogres) : elle est constituée de différentes couches (Figure 1). Il y a la croûte rocheuse en surface, le manteau rocheux en dessous, puis le noyau de fer liquide et enfin tout au centre la graine de fer solide. La température et la pression croissent avec la profondeur jusqu’à atteindre tout au centre près de 6 000 °C, l’équivalent de la température à la surface du Soleil, et 350 GPa, soit plus de 3 200 fois la pression régnant dans la fosse des Mariannes, le point le plus profond des océans. Nous savons cela grâce à l’action combinée des modèles, simulations et expériences de sismologie (l’étude des ondes sismiques, c’est-à-dire les vibrations du sol qui ont lieu lors d’un tremblement de terre par exemple) et de physique des minéraux à hautes pressions (l’étude des transformations des minéraux et de leur propriétés physiques), sans oublier les efforts de plusieurs générations de chercheurs. Néanmoins, beaucoup de travail reste à accomplir pour connaître avec précision les conditions régnant dans chaque couche, ainsi que le comportement physique, mécanique et chimique des différents matériaux les composant.

Cercles concentriques montrant que l'intérieur de la Terre est constitué de plusieurs couches. À chaque limite de couche il y a 3 informations : profondeur (km), température (°C) et Pression (GPa). La couche la plus externe est la Croûte (70km /1100°C /2 GPa). Ensuite, le Manteau supérieur de (70km /1100°C /2 GPa) jusqu'au Manteau inférieur (660km /1500°C /25 GPa). Ce manteau inférieur va lui-même jusqu'au "Noyau externe" (2900km /3800°C /140GPa). Et ce noyau externe va jusqu'au Noyau interne (5100km /5200°C /330GPa). Et le centre de la Terre : 6370km /5500°C /360GPa. — **Figure 1. La Terre et les oignons sont formés de couches concentriques.** Cette illustration des différentes couches formant la Terre donne les valeurs approximatives de pression et température aux différentes interfaces entre deux couches. La croûte et le manteau sont constitués de roches solides. Le noyau métallique est solide en son centre (aussi appelé *graine*) et liquide pour la partie externe.

Étudier le noyau de fer liquide est important pour mieux comprendre comment notre planète s’est formée et a évolué mais aussi par exemple comment le champ magnétique terrestre fonctionne. C’est d’ailleurs ce dernier qui nous protège, nous et notre atmosphère, du vent solaire, ce flux intense de rayonnements et de particules émis par notre étoile, le Soleil. Mais l’étude du centre de la Terre est complexifiée par l’absence d’échantillons qui pourraient nous renseigner sur la composition du noyau terrestre. Contrairement à ce que pourraient nous laisser imaginer Jules Verne ou certains réalisateurs de films, personne n’a réussi (et ne réussira probablement jamais) à atteindre le centre de la Terre. Les forages restent très superficiels et n’atteignent même pas le bas de la croûte : le plus profond jamais réalisé est celui de Kola (en Russie) qui a atteint 12,2 kilomètres de profondeur sous la surface [1]. Quant aux plus profonds échantillons qui nous parviennent naturellement, les péridotites (roches vertes du manteau) et les diamants, ils sont formés à moins de 500 voire 700 km de profondeur. Pour voyager au centre de la Terre il faut donc ruser et réaliser des expériences en laboratoire à très hautes pression et température au moyen, comme c’est le cas dans cette publication, d’une cellule à enclumes de diamant chauffée par laser.

Embarquement immédiat à bord de la cellule à enclumes de diamant

Ce dispositif expérimental, bien connu des minéralogistes, est représenté en Figure 2. Il consiste principalement en deux minuscules diamants (d’environ 1,5 mm de hauteur et qui ne pourraient pas servir en joaillerie car la pointe a été coupée) se faisant face, et qui enserrent une rondelle métallique appelée joint. Ce dernier a son centre percé d’un trou de 200 μm (micromètres) de diamètre, soit environ 2 fois le diamètre d’un cheveu. C’est cette cavité qui forme la chambre de compression : on y place l’échantillon à comprimer ainsi qu’un matériau, liquide ou solide, servant à maintenir une pression homogène dans tout l’échantillon tout en l’isolant thermiquement de l’extérieur. Dans cette étude, c’est du chlorure de potassium ou du saphir en poudre ou en monocristal qui est utilisé. L’échantillon, quant à lui, consiste en une fine tranche de fer pur de 15 à 20 μm d’épaisseur, soit près de 5 fois plus fin qu’un cheveu.

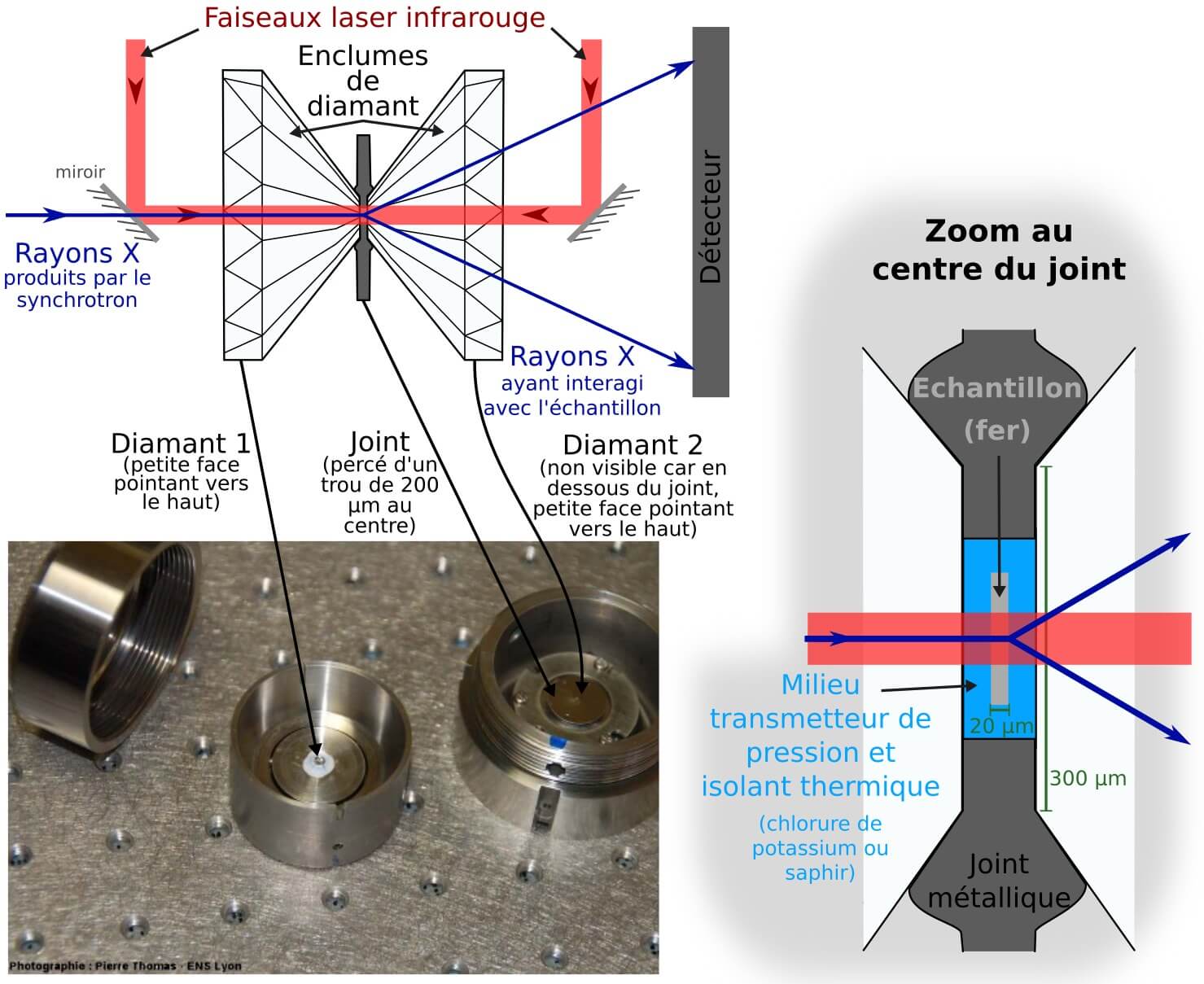
Photographie et schéma d'une enclume à diamant. — **Figure 2. Schéma du dispositif expérimental de cellule à enclumes de diamant avec chauffage par laser et photographie d’une cellule démontée**. L’échantillon de fer pur est placé au centre de la chambre (trou au centre du joint métallique) dans un milieu transmetteur de pression et servant d’isolant thermique. Pour comparaison, le diamètre du trou dans le joint fait environ deux fois celui d’un cheveu. Sur la photo, l’élément au centre s’insère dans celui de droite afin de placer les deux diamants face à face de part et d’autre du joint. Le capot (à gauche) se visse ensuite sur le montage. Le dispositif expérimental peut différer légèrement selon les gammes de pression visées. Crédit photographie : © Pierre Thomas, extraite de l’article Une cellule à enclumes de diamant (Planet-Terre, 2011), avec l’aimable autorisation de l’auteur.

L’un des deux diamants est fixé dans un support immobile appelé cylindre (partie droite sur la photo Figure 2), tandis que l’autre est collé sur la partie mobile, le piston (au milieu sur la photo). Celui-ci s’insère dans le cylindre et est maintenu en place par le capot (à gauche sur la photo) qui vient se visser sur le cylindre. En rapprochant le piston du cylindre par un système de vis de serrage (par exemple) il est possible d’atteindre de très hautes pressions telles que celles régnant dans le manteau terrestre. Dans cet article, les auteurs ont atteint des pressions allant jusqu’à 116 GPa, ce qui correspond presque à la limite noyau-manteau [2] (Figure 1). Une fois l’échantillon comprimé à la pression voulue à température ambiante, il est chauffé par un laser envoyé de part et d’autre du dispositif (Figure 2) jusqu’à être totalement fondu. 14 expériences de ce type ont été réalisées pour atteindre 14 conditions de pression/températures différentes. Pour chaque expérience, un nouvel échantillon de fer pur est utilisé (on ne réutilise pas les échantillons plusieurs fois).

Pour la visite guidée, suivez les rayons X

Ce voyage, qui jusque-là s’est déroulé tranquillement dans le laboratoire, doit maintenant se poursuivre dans un synchrotron, dans le cas présent au Spring-8 dans la province de Hyogo au Japon. Un synchrotron est un instrument scientifique de forme circulaire, mesurant entre plusieurs dizaines ou milliers de mètres de circonférence et produisant des rayons X extrêmement puissants (autrement dit extrêmement énergétiques). Hors de question donc d’utiliser ce rayonnement pour passer une radio si vous ne voulez pas que ce soit la dernière de votre vie ! Les rayons X produits par cette source permettent en revanche d’analyser certaines propriétés de la matière, comme la position des atomes dans un cristal. Cela est possible grâce à un phénomène bien pratique appelé la diffraction. C’est par exemple ce qu’il se passe lorsque l’on regarde une source lumineuse derrière un rideau très fin (Figure 3). Les mailles du voilage sont suffisamment fines pour que les rayons lumineux de la source en arrière-plan soient déviés et interagissent entre eux — on dit qu’ils interfèrent — de façon à former des taches lumineuses et sombres espacées régulièrement. La mesure de l’espacement des taches lumineuses permet, avec la connaissance des paramètres expérimentaux, de retrouver les dimensions de l’obstacle (ici les mailles du voilage).

Photographie du haut : lammpadaires allumés dans une rue. Chaque ampoule fait comme un rond flou blanc. Photographie du bas : chaque ampoule est une grosse tache blanche d'où partent 4 faisceaux blancs pointillés à 90°C les uns des autres. — **Figure 3. Figure de diffraction obtenue avec un voilage (en bas) comparé avec la scène naturelle (en haut).** Les mailles du voilage sont suffisamment fines pour que les rayons lumineux des sources en arrière-plan soient déviés et interagissent entre eux de façon à former des taches lumineuses et sombres espacés régulièrement. Crédit : Christophe.Finot/Wikimédia Commons/CC BY-SA 3.0.

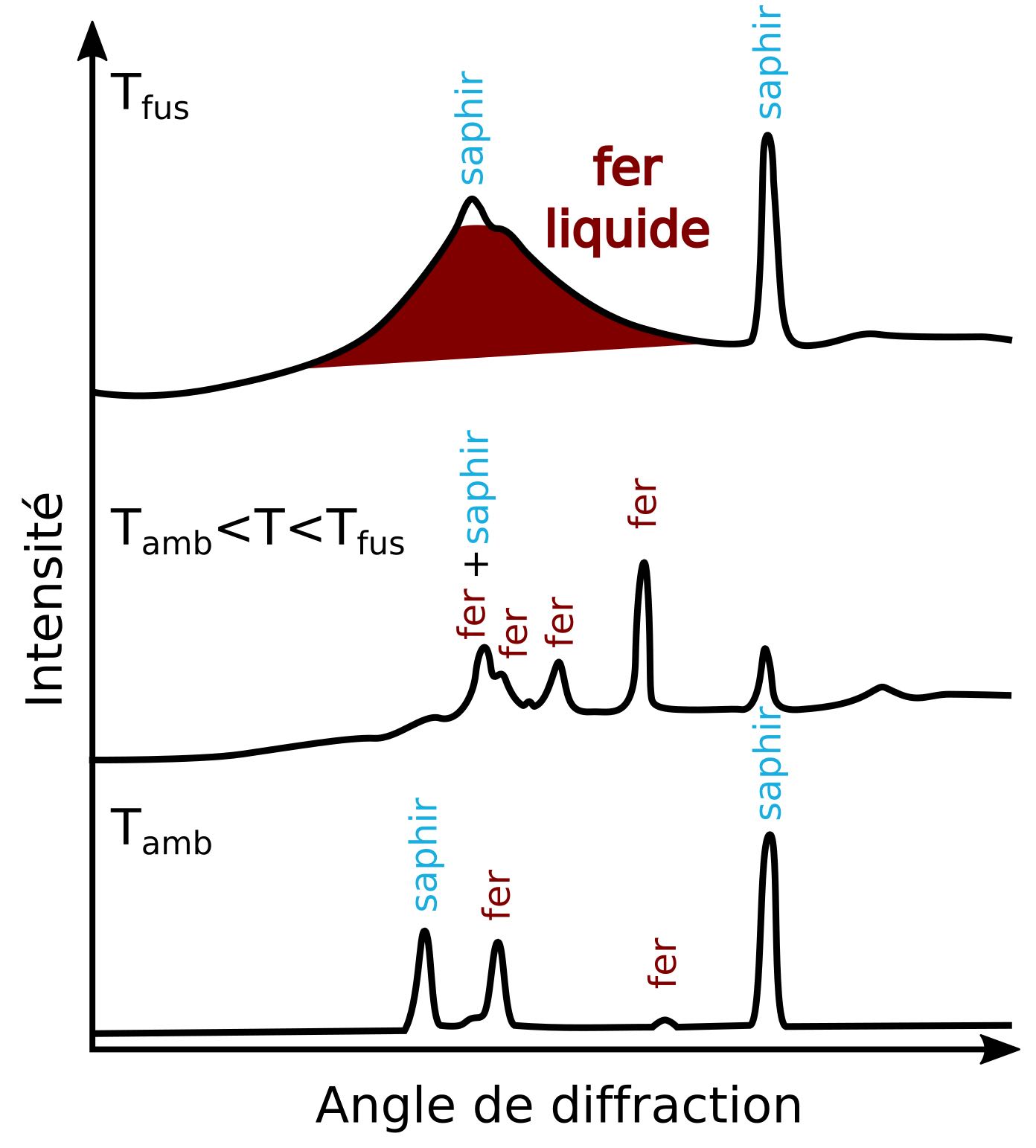
Le principe est donc le même avec les rayons X mais à une échelle beaucoup plus petite. Ainsi, il est possible de trouver l’espacement entre les atomes qui est de l’ordre de l’ångström, soit 0,1 nm (nanomètre). L’intensité de chaque tâche de diffraction est mesurée en fonction de son angle avec le rayon X incident, ce qui donne un graphique tel que présenté en Figure 4 : chaque pic représente une tâche de diffraction. À température ambiante, le fer est solide. Les atomes de fer sont organisés en un arrangement périodique (= qui se répète) ; un nombre fini de pics est donc visible car on a besoin d’un nombre fini d’informations (géométriques et types d’atomes) pour reproduire la totalité du cristal (Figure 4, spectre du bas $T_\mathrm{amb}$ ). Au contraire, sous forme liquide, cet arrangement organisé des atomes est perdu [*], le spectre de diffraction montre alors une large bande (Figure 4, zone rouge).

3 courbes avec différents pics plus ou moins hauts et plus ou moins lisses. — Figure 4. Comparaison schématique de spectres de diffraction X à température ambiante (T_amb) et à la température de fusion du fer (T_fus), c’est-à-dire la température à laquelle le fer devient liquide. Spectres du bas et du milieu : tant que le fer est solide (T_amb et T<T_fus), un nombre fini de raies (de « pics ») est observé car la structure atomique est ordonnée. **Spectre du haut** : quand le fer est fondu (T_fus), seule une large bande est visible car la structure est désordonnée. Notons que le saphir reste solide pendant toute l’expérience et conserve donc ses raies. Image produite à partir des données de la publication originale.

Ce que les auteurs de cette publication sont parvenus à faire, c’est développer une meilleure méthode pour extraire l’information contenue dans cette bande de diffraction. Ils ont ainsi déterminé plus précisément la masse volumique (autrement dit la masse des atomes contenus dans un volume donné) du fer liquide à différentes pressions jusqu’à 116 GPa et différentes températures. Mais nous avons un problème : il est estimé que la pression dans le noyau externe terrestre varie entre 140 et 330 GPa (Figure 1). Alors comment utiliser les résultats obtenus ici, de pressions inférieures à celles du noyau externe, pour analyser ce qu’il s’y passe ? Grâce à l’équation d’état du fer liquide, déterminé à partir des valeurs obtenues.

À votre droite, vous pourrez admirer les équations d’état du fer liquide

Une équation d’état est une fonction mathématique qui relie plusieurs grandeurs thermodynamiques comme la pression, la masse volumique et la température, afin de décrire, ici, le matériau étudié. Les auteurs utilisent l’équation de Mie-Grüneisen (dont la formule vous est épargnée) qui relie la pression à la masse volumique et à la température. Ils ajustent numériquement les paramètres de cette équation pour que les courbes ainsi obtenues (Figure 5a) reproduisent au mieux leurs données et celles de quelques expériences de choc [**] réalisées à plus hautes pressions par d’autres équipes de recherche. En prenant en compte le fait que le noyau de fer liquide, aussi appelé noyau externe, est bien mélangé par les mouvements de convection et en considérant trois températures possibles à l’interface graine-noyau externe, les auteurs déterminent alors l’évolution de la masse volumique avec la pression pour le noyau externe (Figure 5d).

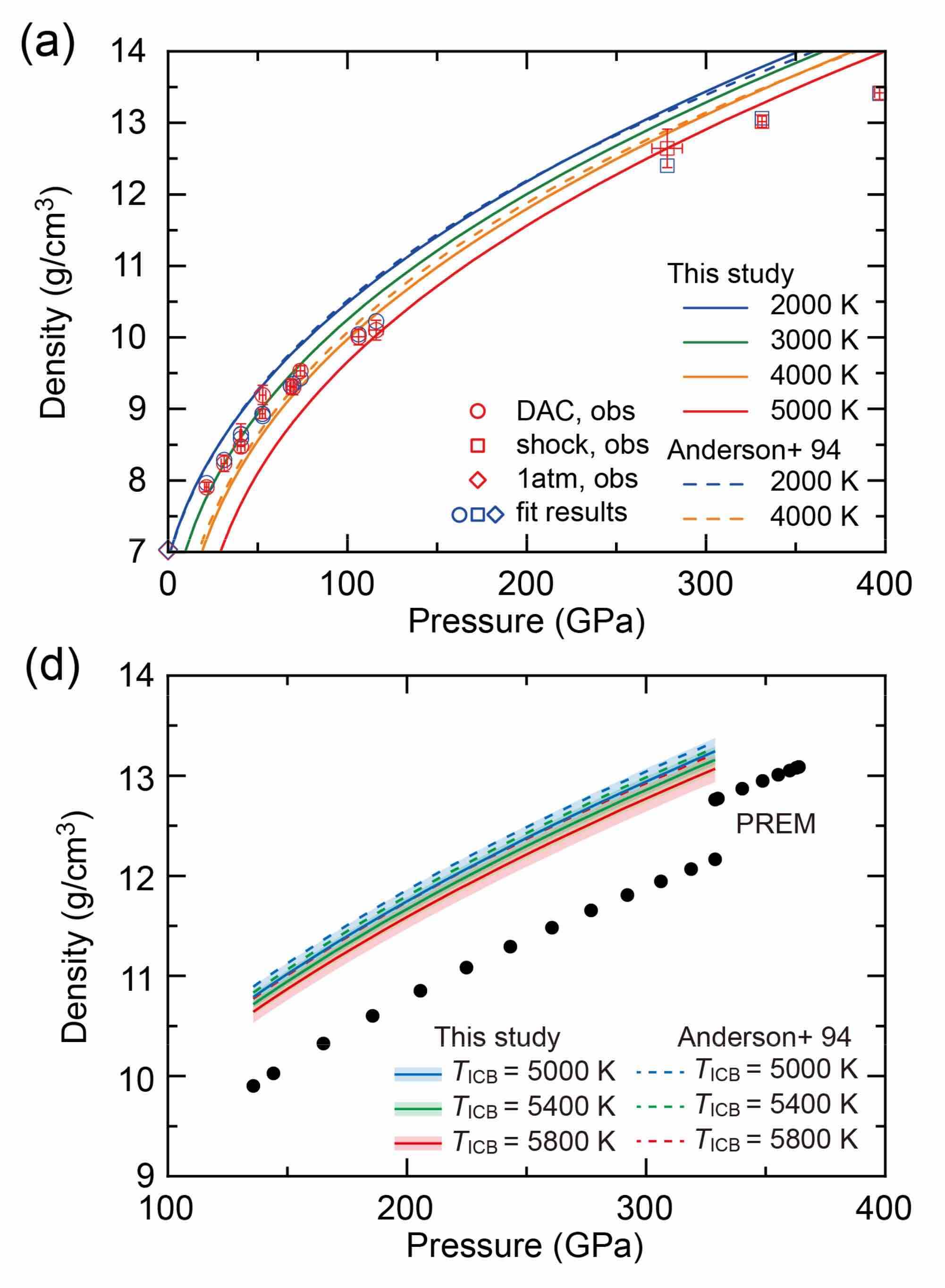
Deux graphiques dont l'abscisse est la perssion (GPa) et l'ordonnée la masse volumique (gramme par centimètre cube). Graphique du haut : des points sont alignés sur des courbes de différentes couleurs. Chaque couleur correspond à une température différente en degré Kelvin. GRaphique du bas, idem, mais les couleurs et températures ne sont pas les mêmes. Des points noirs, alignés selon une courbe, représentent le modèle PREM. Ceux-ci sont décalés mais suivent la même allure que les courbes mesurées. — **Figure 5. Masse volumique (*Density*) en fonction de la pression (*Pressure*) pour le fer liquide. (a)** montre que les équations d’état (les courbes colorées) déterminées par les auteurs reproduisent fidèlement les points expérimentaux : les symboles bleus (valeurs calculées) se superposent aux symboles rouges (valeurs expérimentales). Les courbes colorées en **(d)** représentent l’évolution de la masse volumique avec la pression pour le noyau externe (liquide) de fer, c’est-à-dire en prenant en compte le mélange du noyau par la convection et des températures possibles à l’interface graine-noyau externe (ICB). Leurs résultats sont comparés avec ceux obtenus par le modèle sismique de référence (PREM, point noirs) et montrent un clair décalage entre les deux. Crédit : © tirée de la publication originale, avec l’aimable autorisation de l’un des auteurs et de l’éditeur, https://doi.org/10.1103/PhysRevLett.124.165701.

Vient alors le moment décisif de comparer les résultats obtenus avec le modèle préliminaire de référence de la structure interne de la Terre appelé PREM (Preliminary Reference Earth Model) [***]. C’est grâce à ce modèle de propagation des ondes sismiques développé depuis 1981 [2] que nous avons connaissance de la structure interne de la Terre. La Figure 5d montre qu’il y a une différence flagrante entre les courbes colorées obtenues par les auteurs et le modèle PREM (points noirs) : le noyau externe terrestre est 7 à 8 % moins dense qu’un noyau composé de fer pur. Le résultat de cette observation est donc sans appel et cohérent par rapport aux études précédentes : le noyau externe n’est pas composé uniquement de fer.

Que rajouter dans ce noyau théorique de fer pur pour que les expériences et modèles soient alors conformes à l’observation du noyau terrestre ? [****] La masse volumique qu’il faut obtenir avec le mélange fer-éléments inconnus doit être plus faible que celle du fer pur afin de correspondre aux valeurs données par le modèle PREM. Les éléments légers régulièrement envisagés sont le silicium, l’oxygène, le soufre, le carbone ou l’hydrogène [3]. Les auteurs s’intéressent ici à l’oxygène. Ils estiment que la quantité d’oxygène à rajouter au fer liquide pour annuler la différence entre les expériences et le modèle PREM à l’interface noyau interne-noyau externe ne permet pas de résoudre la totalité de la différence de masse volumique dans tout le noyau externe. Cela signifie donc que, contrairement à ce qui était envisagé dans d’autres études, l’oxygène ne serait pas l’unique élément léger dans le noyau externe.

Fin du voyage, que reste-t-il à visiter ?

Cette publication, comme beaucoup d’autres, est une pierre de plus apportée à l’édifice de la connaissance de la composition de la Terre. La méthode de calcul de la masse volumique qui est développée par les auteurs peut être utilisée pour étudier d’autres matériaux et liquides. Cette amélioration ne suffit cependant pas par elle-même pour atteindre la connaissance complète de l’intérieur de notre planète. Pour aller plus loin et comprendre la nature particulière de ces matériaux sous pression, des améliorations des techniques expérimentales sont effectivement nécessaires.

[*] Il peut rester un ordre des atomes au niveau local, mais à longue distance la structure paraît désordonnée.

[**] Type d’expériences consistant à créer une onde de choc dans le matériau pour lui faire atteindre des pressions et des températures bien plus hautes que celles atteignables par cellule à enclumes de diamant. Ces expériences sont cependant plus coûteuses et compliquées à mettre en place, et l’obtention de certains paramètres comme la température est très compliquée.

[***] Voir le papier mâché sur la publication de 1981 présentant le modèle PREM.

[****] Les scientifiques s’accordent sur un noyau composé principalement de fer ou d’un alliage fer-nickel. Utiliser un alliage fer-nickel à la place du fer pur ne change pas la suite du texte. En effet, le nickel a une masse supérieure au fer. Il faut donc bien ajouter des éléments plus légers que le fer pour diminuer la masse volumique du noyau théorique.

[1] Kozlovsky Y. A. & Adrianov N. I. (ed.), The superdeep well of the Kola Peninsula. Springer Berlin Heidelberg, 1987. DOI : 10.1007/978-3-642-71137-4. [Publication scientifique]

[2] Dziewonski D. W. & Anderson D. L., Preliminary reference Earth model. Phys. Earth Planet. Inter., 1981 DOI : 10.1016/0031-9201(81)90046-7. [Publication scientifique]

[3] Hirose K., et al., Composition and State of the Core. Annu. Rev. Earth Planet. Sci., 2013 DOI : 10.1146/annurev-earth-050212-124007. [Publication scientifique]

Publié le 28/09/2021

Anaïs Kobsch/Papier-Mâché/CC BY-NC-SA 4.0 2021

Texte et images, à l’exception des images soumises à droits d’auteurs différents : voir au cas par cas en légende.

Écriture : Anaïs Kobsch
Relecture scientifique : Lambert Baraut-Guinet
Relecture de forme : Charlotte Remy et Éléonore Pérès

Temps de lecture : environ 14 minutes.
Thématiques : Minéralogie (Géologie)

Publication originale : Kuwayama Y., et al., Equation of State of Liquid Iron under Extreme Conditions, Physical Review Letters, 2020. DOI : 10.1103/PhysRevLett.124.165701
Accès libre sur HAL (pdf).

Pourquoi explorer le centre de la Terre ?

Tout comme les confins de l’Amazonie ou les lointaines galaxies, le centre de la Terre est un territoire inexploré, un inconnu qui continue de fasciner. Certes, nous savons aujourd’hui que la Terre est composée de coquilles sphériques concentriques : la croûte en surface et le manteau en dessous, tous deux de roches solides, puis le noyau métallique constitué d’une partie externe liquide et d’une graine solide au centre. Mais il reste encore de nombreuses zones d’ombre sur les mécanismes de formation et d’évolution planétaire.

Parmi les différentes couches de la Terre, un intérêt tout particulier est porté au noyau externe. En effet, la convection de cette coquille sphérique de métal liquide produit le champ magnétique terrestre par un effet dynamo. Ce champ magnétique nous est d’ailleurs bien utile pour protéger l’atmosphère (et ce qui s’y trouve) du vent solaire. Mais comment étudier cette zone située à plus de 2 900 km sous nos pieds ?

C’est grâce à la sismologie et à la physique des minéraux sous pression que nous avons une bonne idée de la structure interne de la Terre et des conditions extrêmes de pression et de température qui y règnent (plus de 6 000 K et 350 GPa au centre). Mais la détermination de ces conditions implique aussi de connaître la nature des couches profondes de la Terre. Or, les forages restent très superficiels et n’atteignent même pas le bas de la croûte. Le plus profond jamais réalisé est celui de Kola (Russie) qui a atteint 12,2 kilomètres sous la surface [1]. Quant aux plus profonds échantillons qui nous parviennent naturellement, les péridotites (roches issues du manteau) et les diamants, ils sont formés à moins de 500 voire 700 km de profondeur.

Les scientifiques s’accordent sur un noyau composé principalement de fer (ou d’un alliage fer-nickel). Depuis les années 1950, grâce aux observations sismiques et à des modélisations, un déficit de densité est identifié entre le noyau tel qu’il est observé et le fer pur aux mêmes conditions de pression et de température. Ce déficit a été rapidement attribué à la présence d’éléments plus légers que le fer dans le noyau. L’identification précise du type d’éléments et de leur concentration est importante aussi bien pour comprendre la formation de la Terre ou son refroidissement que la génération de la dynamo terrestre par exemple [2]. La présence d’autres éléments chimiques dans le fer modifie en effet sa température de fusion ou peut influer sur la convection dans le noyau externe. Dans la publication discutée ici, les chercheurs s’intéressent à la présence d’oxygène dans le noyau. Pour apporter des améliorations notables aux modèles utilisés pour estimer la teneur en éléments légers dans le noyau, ils réalisent des expériences en laboratoire sur du fer pur jusqu’à des pressions et températures proches de celles régnant au sommet du noyau externe.

Une expérience à très hautes pression et température : LH-DAC

Pour parvenir à leurs fins, les auteurs utilisent un dispositif expérimental bien connu en minéralogie expérimentale : la cellule à enclumes de diamant couplée à un chauffage par laser. Comme représenté sur la Figure 1, ce dispositif consiste en l’utilisation de deux diamants (d’environ 1,5 mm de hauteur et quelques centaines de micromètres à la base) pour comprimer un joint métallique (ici en rhénium) dans lequel un trou a été percé. Ce trou, d’un diamètre d’environ 200 μm ou moins, constitue la chambre de compression dans laquelle l’échantillon de fer d’à peine 15-20 μm d’épaisseur est placé. Un matériau servant d’isolant thermique et permettant d’obtenir une pression homogène dans toute la chambre est enfin ajouté. Il s’agit ici de saphir en poudre ou en monocristal ou bien de chlorure de potassium KCl en poudre.

La compression du joint par les diamants a permis d’atteindre des pressions allant jusqu’à 116 GPa, ce qui correspond presque à la limite noyau-manteau [3]. Une fois l’échantillon comprimé à la pression voulue à température ambiante, il a été chauffé par un laser infrarouge envoyé de part et d’autre du dispositif (Figure 1) jusqu’à atteindre son point de fusion et même au-delà. 14 expériences de ce type ont été réalisées, chacune avec un nouvel échantillon de fer pur n’ayant pas déjà été utilisé dans une expérience.

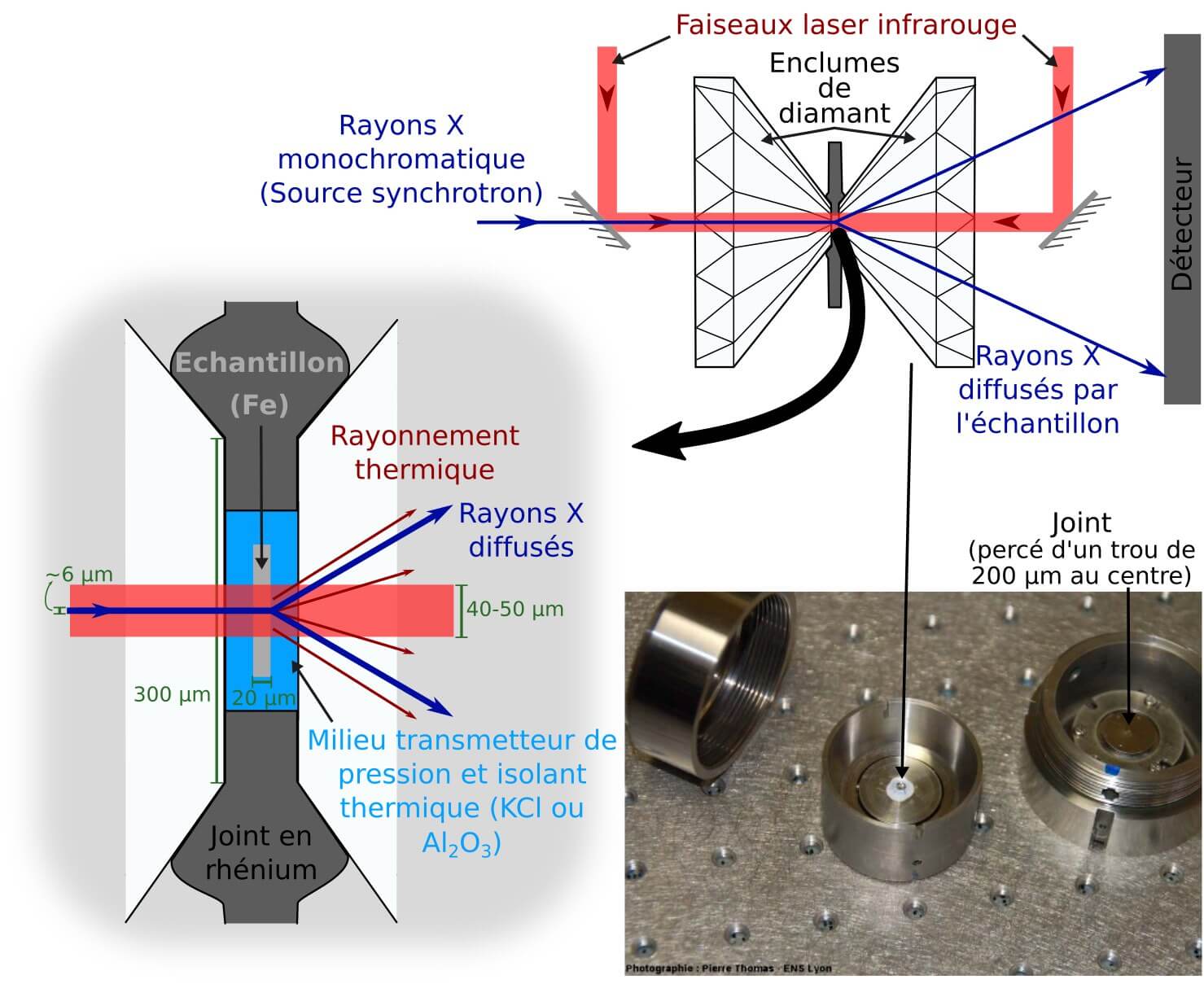
La température a été mesurée grâce au spectre d’émission thermique de la zone chauffée (environ 40-50 μm). La pression, quant à elle, a été calculée à partir du volume de la maille élémentaire du fer sous la forme fcc (cubique à faces centrées), volume obtenu grâce au spectre de diffraction X du fer juste avant sa fusion. C’est d’ailleurs la diffraction des rayons X qui a été également utilisée pour obtenir la masse volumique ( $\rho$ ). Pour comprendre comment, quelques informations sur cette technique s’imposent.

Une interaction particulière de la matière avec les rayons X : la diffusion

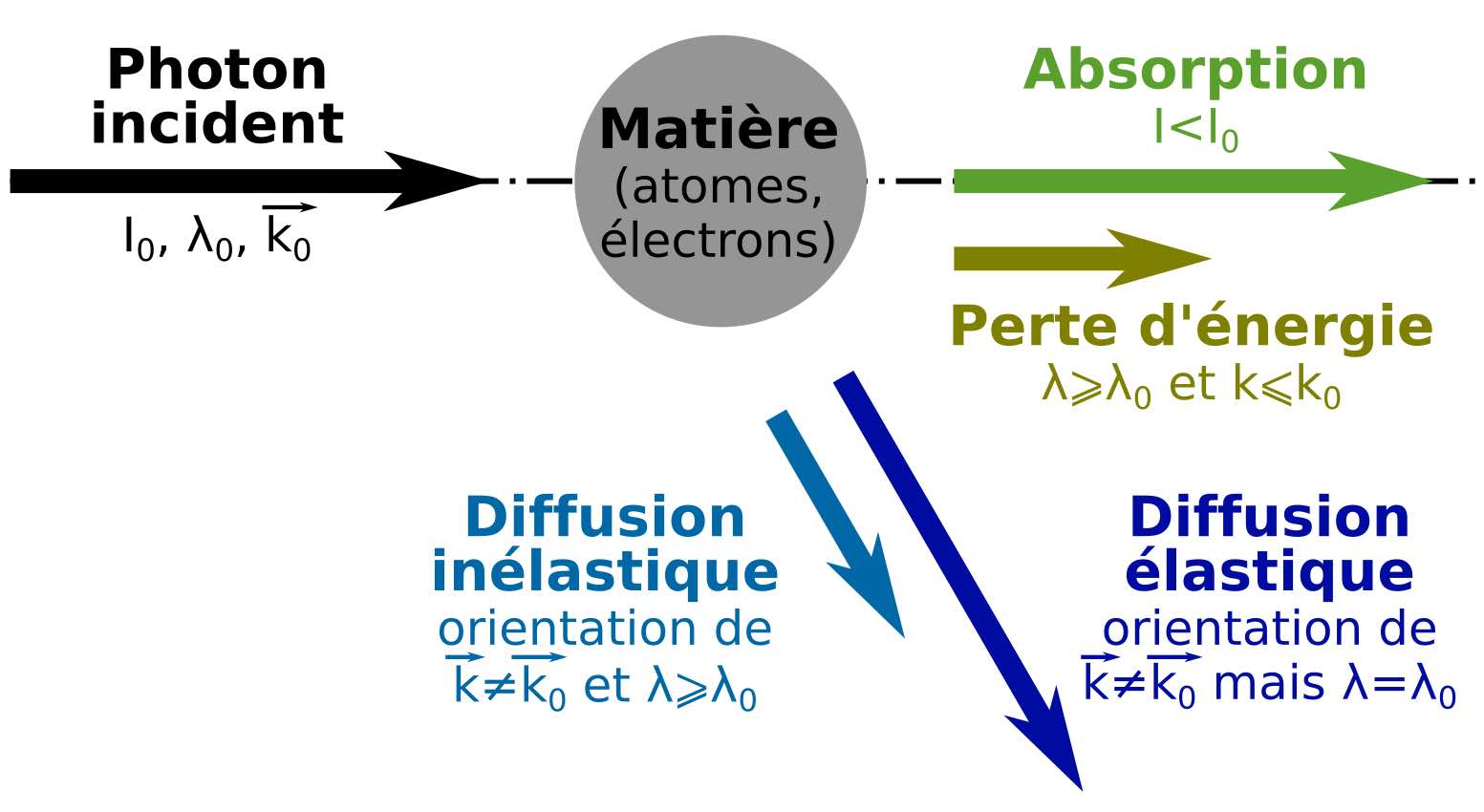
Oui vous avez bien lu, je parle ici de la diffusion des rayons X, et non de la diffraction, car cette dernière n’est qu’une forme particulière de la première. Reprenons depuis le début : lorsqu’un rayonnement électromagnétique rencontre de la matière, il interagit avec elle. Le rayonnement mesuré après l’interaction est différent du rayonnement incident. Les modifications observées sont dues à des phénomènes d’absorption, de perte d’énergie, de modification de la matière ou de diffusion dans le matériau étudié. En général, plusieurs effets ont lieu en même temps, c’est pourquoi tout l’art de l’expérimentateur est de trouver la meilleure manière de détecter celui qui l’intéresse sans être perturbé par les autres.

Dans la publication qui nous intéresse, l’effet qui est étudié est la diffusion des rayons X. De manière générale, la diffusion correspond à la modification de la direction du vecteur d’onde (Figure 2). On distingue la diffusion inélastique pour laquelle il y a en plus modification de l’énergie de l’onde incidente, de la diffusion élastique qui se produit sans changement de l’énergie. Dans les conditions adéquates (longueur d’onde de l’ordre de l’ångström), la diffusion élastique produite par un cristal donne lieu au phénomène d’interférence appelé diffraction.

La légende décrit la figure. — **Figure 2. Représentation schématique de quelques interactions matière-rayonnement électromagnétique.** L’intensité (I), la longueur d’onde (λ) et le nombre d’onde (k) varient ou non selon le type d’interaction. Le rayonnement incident est diffusé lorsqu’il change de direction de propagation (orientation du vecteur k différente). La diffusion inélastique comporte en plus un changement d’énergie de l’onde par rapport à la diffusion élastique (longueur d’onde λ) différente.

L’intensité des rayons X diffractés par l’échantillon est mesurée en fonction de l’angle entre les rayons d’entrée et de sortie. Pour un solide cristallin, dans lequel les atomes sont bien ordonnés, le spectre de diffraction montre des raies bien nettes qui permettent de retrouver la structure cristallographique (géométrie du cristal, types d’atomes, etc.). Pour un liquide, au contraire, nous n’avons qu’une bande très large (Figure 3, zone rouge). En effet, bien qu’un liquide ne soit pas ordonné à longue distance, il y a quand même une organisation locale des atomes. Et c’est cette organisation qu’il est possible d’extraire du spectre de diffraction X du liquide afin d’obtenir la masse volumique.

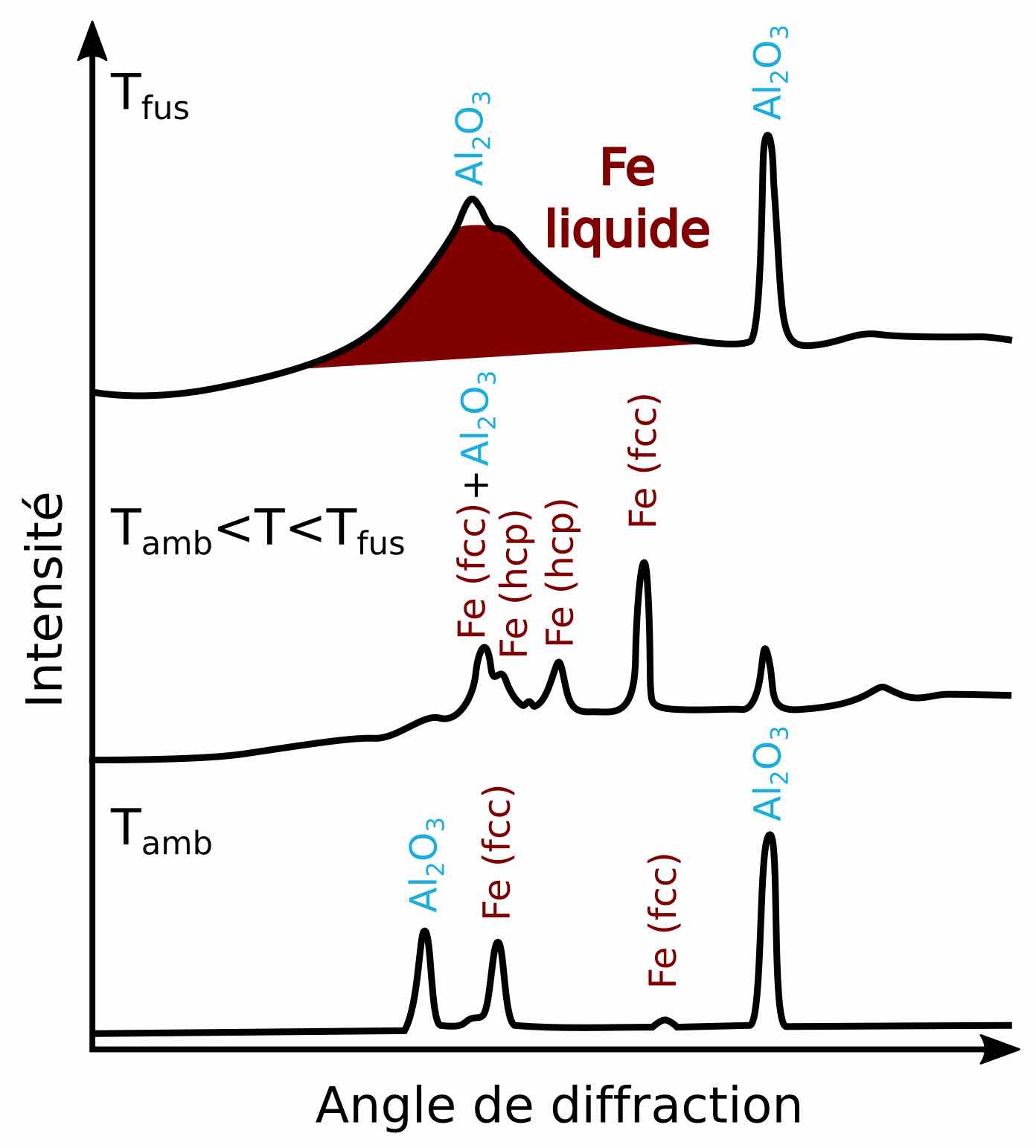
Une meilleure façon d’obtenir la masse volumique

La première étape consiste donc à obtenir le signal correspondant uniquement à la diffusion des rayons X par le liquide (Figure 3, zone rouge). Pour cela, il suffit de soustraire l’intensité du spectre de diffraction X, enregistré juste avant la fusion du fer, au spectre de diffraction X enregistré au-dessus de la fusion. L’intensité obtenue est exprimée en fonction du moment de diffusion $Q$ , qui est équivalent au rapport entre l’angle de diffraction et la longueur d’onde des rayons X en entrée. Utiliser $Q$ comme variable plutôt que l’angle de diffraction est bien utile pour comparer des résultats acquis avec des sources de rayons X différentes, car lorsque la longueur d’onde des rayons X est changée, les angles des pics de diffraction le sont aussi.

Cette intensité $I(Q)$ est ensuite convertie en une grandeur appelée facteur de structure $S(Q)$ , qui permet de calculer la fonction de distribution des atomes dans le liquide (leur probabilité de présence en fonction d’une distance radiale) et ainsi d’obtenir la masse volumique. Mais pour ce faire, ces calculs requièrent une intégration sur le moment de diffusion $Q$ allant de 0 à l’infini, or $S(Q)$ n’est mesuré que pour des valeurs finies du moment de diffusion ( $Q \le Q_{max}$ ). Si le calcul n’est réalisé qu’avec les valeurs de $S(Q)$ pour $Q \le Q_{max}$ , alors d’importantes erreurs sur la masse volumique sont à prévoir !

Pour remédier à ce problème, les auteurs ont cherché la fonction mathématique qui permet de prolonger au mieux $S(Q)$ jusqu’à l’infini. Après cinq pages d’explications et de tests mathématiques [*], ils ont leur nouvelle fonction $S_{étendu}(Q)$ définie de 0 à l’infini :

$S_{étendu}(Q) =S(Q)$ obtenu par conversion de $I(Q)$ pour $Q \le Q_{max}$

= fonction mathématique adaptée au système étudié pour $Q > Q_{max}$

Grâce à cette méthode, ils réussissent à obtenir des masses volumiques pour le fer liquide avec moins de 1 % d’erreur.

Les équations d’état, c’est la vie (pour le minéralogiste)

Nous avons donc la masse volumique du fer liquide pour différentes valeurs de pression jusqu’à 116 GPa, et de température jusqu’à 4 340 K. En analysant les spectres de diffusion inélastique des rayons X (l’autre type de diffusion décrite plus haut), les auteurs obtiennent également la vitesse des ondes sismiques P ( $V_\mathrm{P}$ ) jusqu’à 45 GPa et 2 700 K. Mais nous avons un problème : il est estimé que la pression dans le noyau externe terrestre varie entre 135 et 330 GPa, tandis que la température augmente de 4 000 à 5 000-5 800 K entre l’interface noyau manteau et l’interface avec le noyau interne. Alors comment comparer les résultats obtenus ici, de pressions et températures inférieures à celles du noyau externe, avec les données issues des modèles sismiques appliqués au noyau externe ? La réponse est dans le titre de cette partie : les équations d’état.

Une équation d’état est une fonction mathématique qui relie plusieurs grandeurs thermodynamiques ( $P$ , $T$ , $\rho$ , etc.) servant à décrire le système étudié. Les auteurs ajustent les paramètres des équations de Mie-Grüneisen [**] pour que les équations ainsi obtenues reproduisent au mieux leurs données et celles de quelques expériences de choc [***] réalisées à plus hautes pressions par d’autres chercheurs. Nous voyons sur la Figure 4a et 4b que cette technique marche plutôt bien : les pressions calculées à partir de $\rho$ et $V_\mathrm{P}$ mesurées sont en bon accord avec les pressions mesurées (les symboles bleus sont quasiment tous superposés aux symboles rouges, respectivement).

Mais le travail ne s’arrête pas là ! Nous savons que le noyau de fer liquide est bien mélangé grâce aux mouvements de convection qui l’animent et créent le champ magnétique. Dans ces conditions (un système homogénéisé), il est possible de décrire la température en fonction de la pression à l’aide d’un profil dit adiabatique ou isentropique. Celui-ci est calculé et tracé Figure 4c pour trois températures possibles à la base du noyau, car une grosse incertitude subsiste quant à la température à l’interface entre la graine et le noyau externe (en anglais ICB pour Inner Core Boundary). C’est enfin grâce au calcul de ce profil de température que les masses volumiques et vitesses sismiques sont obtenues pour la totalité du noyau externe (Figure 4d et 4e).

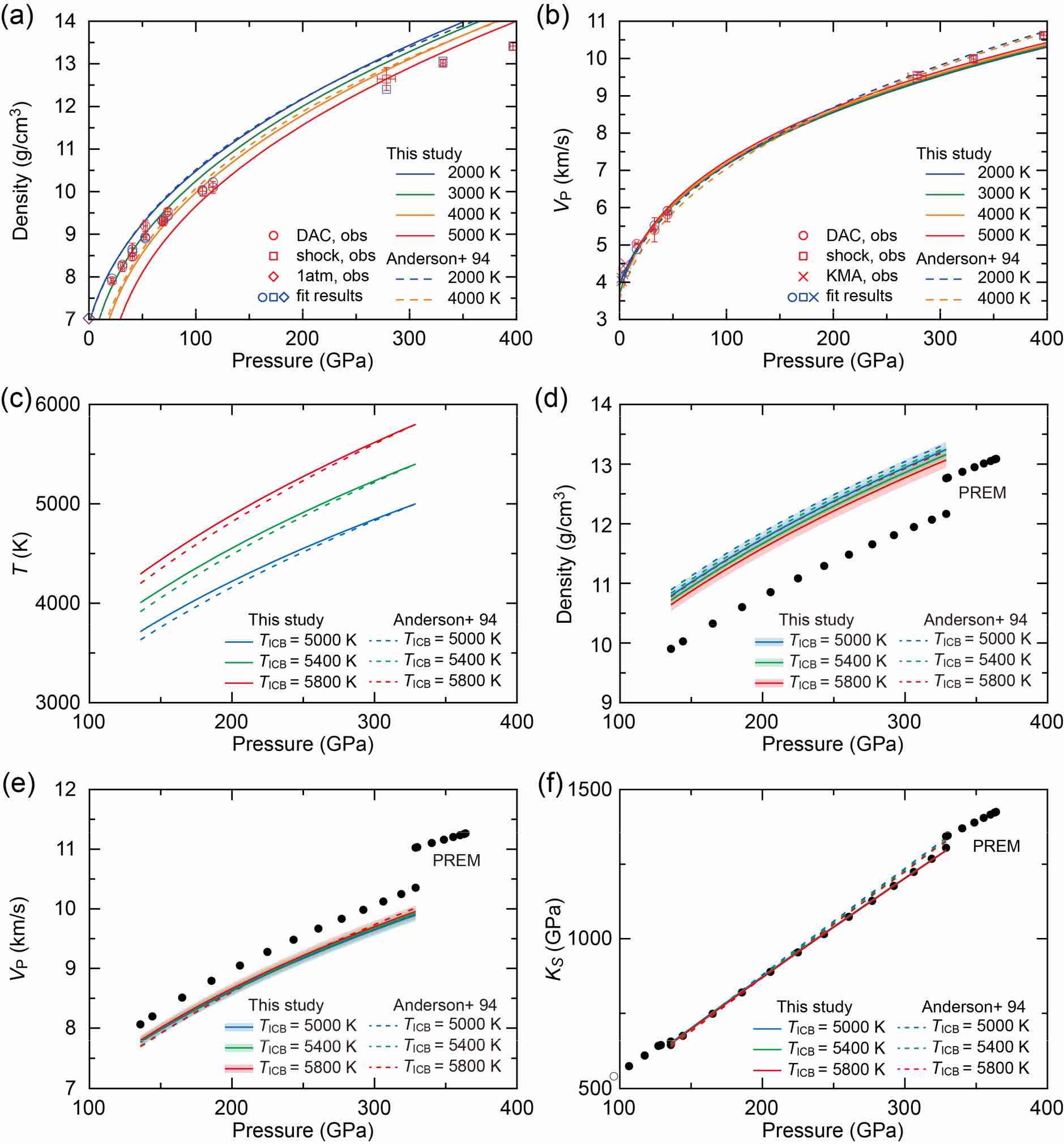
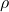Sur les six graphiques, les courbes ont des allures proches, et on observe des points alignés sur les courbes. Graphiques d et e : des points noirs correspondant au modèle PREM sont décalés mais suivent l'évolution des courbes. Graphiques f : les points noirs sont alignés sur les droites mesurées. — **Figure 4. Masse volumique (*Density* $\rho$ ), vitesse sismique des ondes P (V_P) et coefficient de compressibilité adiabatique (**K_S**) pour le fer liquide.** **(a)** et **(b)** montrent que les équations d’état obtenues (courbes continues tracées en fonction de la pression) reproduisent fidèlement les pressions des masses volumiques et vitesses sismiques des points expérimentaux : les symboles bleus (valeurs calculées) se superposent aux symboles rouges (valeurs expérimentales). **(c)** montre les équations d’état recalculées pour trois températures possibles de l’interface graine-noyau externe (ICB), dans le cas d’un noyau de fer liquide bien mélangé par la convection (adiabatique). Enfin, **(d)**, **(e)** et **(f)** donnent l’évolution de 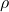*$\rho$* , V_P et K_S avec la pression pour le noyau de fer liquide, et comparent ces résultats avec ceux obtenus par le modèle sismique Preliminary Reference Earth Model (PREM). Crédit : © tirée de la publication originale, avec l’aimable autorisation de l’un des auteurs et de l’éditeur, https://doi.org/10.1103/PhysRevLett.124.165701.

En quoi l’équation d’état du fer liquide nous renseigne-t-elle sur la composition du noyau externe terrestre ?

La structure interne de la Terre est connue grâce au modèle préliminaire de référence appelé PREM (Preliminary Reference Earth Model). Ce modèle de propagation des ondes sismiques, développé depuis 1981 [3] [****], donne entre autres $\rho$ et $V_\mathrm{P}$ en fonction de la profondeur. En convertissant cette dernière en pression, il est possible de comparer $\rho$ et $V_\mathrm{P}$ obtenues pour le fer liquide expérimentalement avec les valeurs du noyau externe terrestre estimées par la sismologie. La Figure 4d et 4e montre qu’il y a une différence flagrante entre les deux valeurs : le noyau externe terrestre est 7 à 8 % moins dense qu’un noyau composé de fer pur, et les ondes P s’y déplacent environ 4 % plus vite que dans un noyau de fer pur. Le résultat de cette observation est donc sans appel et cohérent par rapport aux études précédentes : le noyau externe n’est pas composé uniquement de fer.

Alors que rajouter dedans ? La masse volumique qu’il faut obtenir avec le mélange fer-éléments inconnus doit être plus faible que celle du fer pur afin de correspondre aux valeurs données par PREM. Les éléments légers régulièrement envisagés sont le silicium, l’oxygène, le soufre, le carbone ou l’hydrogène [4]. Les auteurs s’intéressent ici à l’oxygène. Grâce à leur équation d’état, ils estiment qu’il faudrait rajouter au fer liquide entre 1,6 et 3,8 % en masse d’oxygène pour reproduire la masse volumique observée par le modèle PREM à l’interface noyau interne-noyau externe. Cependant, cette quantité d’oxygène n’est pas suffisante pour résoudre la totalité de la différence de masse volumique dans tout le noyau externe. Cela signifie donc que, contrairement à ce qui était envisagé dans d’autres études, l’oxygène ne serait pas l’unique élément léger dans le noyau externe. La méthode développée dans cet article peut maintenant être utilisée pour étudier d’autres matériaux et liquides, mais des améliorations des techniques expérimentales sont nécessaires pour mieux comprendre la nature particulière de ces matériaux sous pression.

Du chemin reste encore à parcourir avant de connaître la composition exacte de notre planète, mais une chose est certaine, c’est grâce à l’association d’études de ce type que nous finirons un jour par s’approcher de la solution.

[*] Détaillées dans les supplementary de la publication.

[**] Ces équations donnent la pression en fonction de $\rho$ et $T$ d’une part, et la pression en fonction de $V_\mathrm{P}$ et $T$ d’autre part.

[***] Type d’expériences consistant à créer une onde de choc dans le matériau pour lui faire atteindre des pressions et des températures bien plus hautes que celles atteignables par cellule à enclumes de diamant. Ces expériences sont cependant plus coûteuses et compliquées à mettre en place, et l’obtention de certains paramètres comme la température est très compliquée.

[****] Voir le papier mâché sur la publication de 1981 présentant le modèle PREM.

[1] Kozlovsky Y. A. & Adrianov N. I. (ed.), The superdeep well of the Kola Peninsula. Springer Berlin Heidelberg, 1987. DOI : 10.1007/978-3-642-71137-4. [Publication scientifique]

[2] Poirier J.-P., Light elements in the Earth’s outer core: A critical review. Phys. Earth Planet. Inter., 1994 DOI : 10.1016/0031-9201(94)90120-1. [Publication scientifique]

[3] Dziewonski D. W. & Anderson D. L., Preliminary reference Earth model. Phys. Earth Planet. Inter., 1981 DOI : 10.1016/0031-9201(81)90046-7. [Publication scientifique]

[4] Hirose K., et al., Composition and State of the Core. Annu. Rev. Earth Planet. Sci., 2013 DOI : 10.1146/annurev-earth-050212-124007. [Publication scientifique]

Publié le 28/09/2021

Anaïs Kobsch/Papier-Mâché/CC BY-NC-SA 4.0 2021

Texte et images, à l’exception des images soumises à droits d’auteurs différents : voir au cas par cas en légende.

La publication scientifique facile à digérer !